
例1画出函数y=2sinx xÎR;y=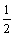 sinx xÎR的图象(简图)
sinx xÎR的图象(简图)
解:画简图,我们用“五点法”
∵这两个函数都是周期函数,且周期为2π
∴我们先画它们在[0,2π]上的简图 列表:
列表:
|
x |
0 |
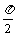 |
p |
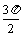 |
2p |
|
sinx |
0 |
1 |
0 |
-1 |
0 |
|
2sinx |
0 |
2 |
0 |
-2 |
0 |
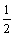 sinx sinx |
0 |
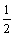 |
0 |
-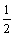 |
0 |
作图:
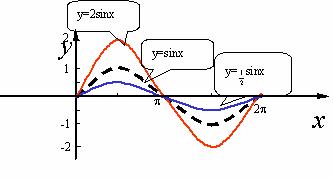
(1)y=2sinx,x∈R的值域是[-2,2]
图象可看作把y=sinx,x∈R上所有点的纵坐标伸长到原来的2倍而得(横坐标不变)
(2)y=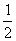 sinx,x∈R的值域是[-
sinx,x∈R的值域是[-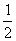 ,
,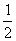 ]
]
图象可看作把y=sinx,x∈R上所有点的纵坐标缩短到原来的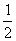 倍而得(横坐标不变)
倍而得(横坐标不变)
引导,观察,启发:与y=sinx的图象作比较,结论:
1.y=Asinx,xÎR(A>0且A¹1)的图象可以看作把正数曲线上的所有点的纵坐标伸长(A>1)或缩短(0<A<1)到原来的A倍得到的
21. (13分) 已知函数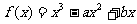 .
.
(1)若函数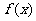 在点(2,
在点(2,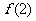 )的切线方程为
)的切线方程为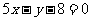 ,求函数
,求函数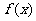 的单调递增区间;
的单调递增区间;
(2)若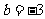 ,
,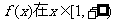 上是增函数,求实数
上是增函数,求实数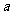 的取值范围。
的取值范围。
20. (13分)已知奇函数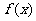 的定义域是
的定义域是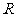 ,且
,且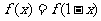 ,当0≤x≤
,当0≤x≤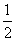 时,
时,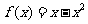 .
.
(1)求证: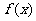 是周期函数;
是周期函数;
(2)求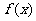 在区间
在区间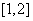 上的解析式;
上的解析式;
(3)求方程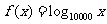 的根的个数.
的根的个数.
19. (13分)在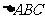 中,
中,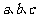 分别为角
分别为角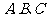 的对边,且满足
的对边,且满足 .
.
(1)求角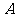 的值;
的值;
(2)若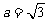 ,设角
,设角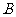 的大小为
的大小为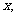
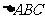 的周长为
的周长为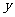 ,求
,求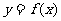 的最大值.
的最大值.
18. (12分)某企业投入81万元经销某产品,经销时间共60个月,市场调查表明,该企业在经销这个产品期间第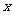 个月的利润
个月的利润 (单位:万元)。为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第
(单位:万元)。为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第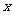 个月的当月利润率为
个月的当月利润率为 ,例如:
,例如: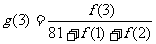 。
。
(1)求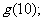
(2)求第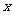 个月的当月利润率
个月的当月利润率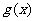 ;
;
(3)该企业经销此产品期间,哪一个月的当前月利润率最大?并求该月的当前利润率。
17. (12分) 已知函数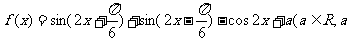 为常数).
为常数).
(1)求函数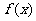 的最小正周期;
的最小正周期;
(2)求函数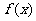 的单调递增区间;
的单调递增区间;
(3) 若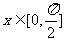 时,
时,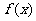 的最小值为
的最小值为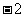 ,求
,求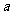 的值.
的值.
16.(12分) 已知命题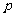 :方程
:方程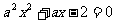 在[-1,1]上有解;命题
在[-1,1]上有解;命题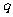 :只有一个
:只有一个
实数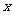 满足不等式
满足不等式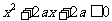 ,若命题“p或q”是假命题,求实数a的取值范围.
,若命题“p或q”是假命题,求实数a的取值范围.
15.给出下列五个命题:
(1)函数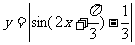 的最小正周期是
的最小正周期是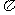 。
。
(2)函数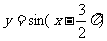 在区间
在区间 上单调递增;
上单调递增;
(3)直线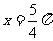 是函数
是函数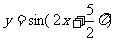 的图象的一条对称轴;
的图象的一条对称轴;
(4)函数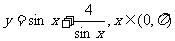 的最小值为
的最小值为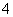 ;
;
(5)函数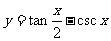 的一个对称中心为点
的一个对称中心为点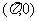 。
。
其中正确命题的序号为______________.
14. 如果二次方程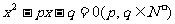 的正根小于3, 那么这样的二次方程有______个。
的正根小于3, 那么这样的二次方程有______个。
13. 若函数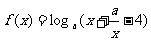 ,(
,( 且
且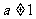 )的值域为
)的值域为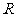 ,则实数
,则实数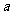 的取值范围是 __________________。
的取值范围是 __________________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com