
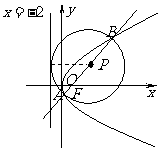
问题1.(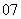 北京)矩形
北京)矩形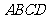 的两条对角线相交于点
的两条对角线相交于点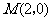 ,
,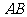 边所在直线的方程为
边所在直线的方程为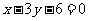 ,点
,点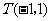 在
在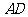 边所在直线上.
边所在直线上.
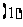 求
求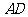 边所在直线的方程;
边所在直线的方程;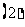 求矩形
求矩形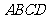 外接圆的方程;
外接圆的方程;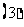 若动圆
若动圆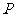 过点
过点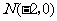 ,且与矩形
,且与矩形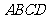 的外接圆外切,求动圆
的外接圆外切,求动圆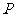 的圆心的轨迹方程.
的圆心的轨迹方程.
 问题2.(
问题2.( 福建)如图,已知点
福建)如图,已知点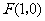 ,
,
直线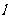 :
: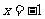 ,
,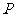 为平面上的动点,过
为平面上的动点,过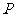 作直线
作直线
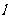 的垂线,垂足为点
的垂线,垂足为点 ,且
,且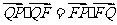 .
.
(Ⅰ)求动点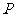 的轨迹
的轨迹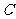 的方程;
的方程;
(Ⅱ)过点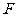 的直线交轨迹
的直线交轨迹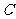 于
于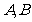 两点,交直线
两点,交直线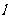
于点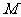 ,已知
,已知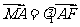 ,
,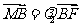 ,求
,求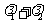 的值;
的值;
问题3.倾斜角为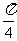 的直线交椭圆
的直线交椭圆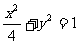 于
于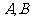 两点,求线段
两点,求线段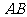 中点的轨迹方程
中点的轨迹方程
问题4. 双曲线
双曲线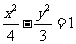 关于直线
关于直线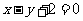 对称的曲线方程是
对称的曲线方程是
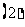 已知抛物线
已知抛物线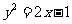 ,
,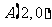 .问是否存在过
.问是否存在过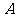 点的直线
点的直线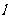 ,使抛物线上存在不同的两点关于直线
,使抛物线上存在不同的两点关于直线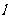 对称?如果存在,求出直线
对称?如果存在,求出直线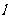 斜率的取值范围;如果不存在,请说明理由.
斜率的取值范围;如果不存在,请说明理由.
 求轨迹方程常用的方法:
求轨迹方程常用的方法: 定义法;
定义法; 利用图形的几何性质;
利用图形的几何性质; 轨迹法;
轨迹法;  参数法;
参数法; 代入法;
代入法; 待定系数法;
待定系数法; 交轨法;
交轨法; 向量法.要注意“查漏补缺,剔除多余”.
向量法.要注意“查漏补缺,剔除多余”.
 对称分为中心对称和轴对称.中心对称问题常利用中点坐标公式解决;解决轴对称问题常根据下列两个条件:①垂直.即已知点和对称点的连线与对称轴垂直;②中点.即已知点和对称点的中点在对称轴上.
对称分为中心对称和轴对称.中心对称问题常利用中点坐标公式解决;解决轴对称问题常根据下列两个条件:①垂直.即已知点和对称点的连线与对称轴垂直;②中点.即已知点和对称点的中点在对称轴上.
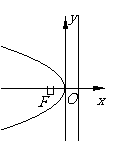
 (
( 福建)已知双曲线
福建)已知双曲线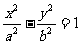 (
(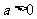 ,
,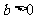 )的右焦点为
)的右焦点为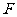 ,若过点
,若过点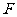 且
且
倾斜角为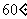 的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
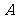
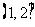
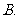
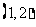
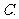
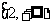

 (
( 全国Ⅰ)已知椭圆
全国Ⅰ)已知椭圆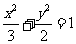 的左、右焦点分别为
的左、右焦点分别为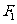 ,
,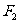 .过
.过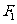 的直线交椭圆于
的直线交椭圆于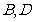 两点,过
两点,过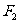 的直线交椭圆于
的直线交椭圆于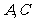 两点,且
两点,且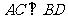 ,垂足为
,垂足为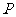 .
.
(Ⅰ)设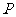 点的坐标为
点的坐标为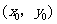 ,证明:
,证明: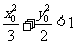 ;
;
(Ⅱ)求四边形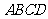 的面积的最小值.
的面积的最小值.
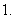 (
( 南通九校联考)过双曲线
南通九校联考)过双曲线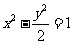 的右焦点作直线
的右焦点作直线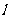 交双曲线于
交双曲线于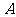 、
、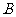 两点,
两点,
若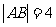 ,则满足条件的直线
,则满足条件的直线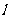 有
有 
 条
条 
 条
条 
 条
条  无数条
无数条
 已知双曲线
已知双曲线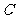 :
: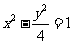 ,过点
,过点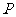
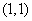 作直线
作直线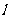 ,使
,使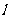 与
与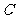 有且只有一个公共点,
有且只有一个公共点,
则满足上述条件的直线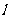 共有
共有 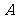
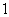 条
条 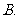
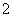 条
条 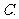
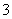 条
条

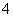 条
条
 (
( 北京海淀区)若不论
北京海淀区)若不论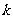 为何值,直线
为何值,直线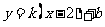 与直线
与直线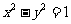 总有公共点,则
总有公共点,则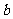 的取值范围是
的取值范围是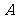
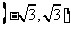
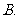
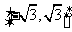
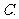
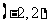


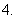 直线
直线 与椭圆
与椭圆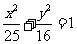 公共点的个数是
公共点的个数是
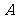
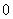
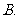
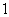
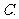
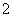
 随
随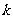 变化而改变
变化而改变
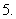 椭圆
椭圆 与直线
与直线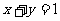 交于
交于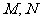 两点,
两点, 的中点为
的中点为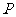 ,且
,且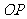 的斜率
的斜率
为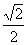 ,则
,则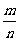 的值为
的值为 
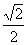
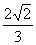
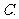
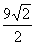

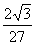
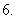 已知椭圆
已知椭圆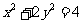 ,则以
,则以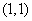 为中点的弦的长度是
为中点的弦的长度是
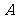
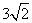
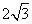
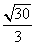

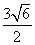
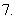 若直线
若直线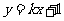 和椭圆
和椭圆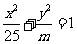 恒有公共点,则实数
恒有公共点,则实数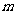 的取值范围为
的取值范围为
 过椭圆
过椭圆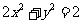 的一个焦点的直线交椭圆于
的一个焦点的直线交椭圆于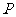 、
、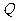 两点,求
两点,求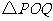 面积的最大值
面积的最大值
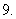 中心在原点,焦点在
中心在原点,焦点在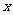 轴上的椭圆的左焦点为
轴上的椭圆的左焦点为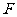 ,离心率为
,离心率为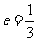 ,过
,过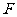 作直线
作直线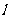 交
交
椭圆于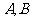 两点,已知线段
两点,已知线段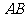 的中点到椭圆左准线的距离是
的中点到椭圆左准线的距离是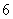 ,则
,则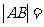
 已知双曲线的方程为
已知双曲线的方程为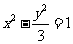 .
. 求以点
求以点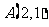 为中点的弦所在的直线方程;
为中点的弦所在的直线方程;
 以点
以点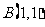 为中点的弦是否存在?若存在,求出弦所在的直线方程;若不存在,
为中点的弦是否存在?若存在,求出弦所在的直线方程;若不存在,
请说明理由.
问题1.设直线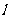 过双曲线
过双曲线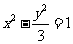 的一个焦点,交双曲线于
的一个焦点,交双曲线于 、
、 两点,
两点, 为坐标原点,若
为坐标原点,若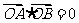 ,求
,求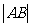 的值.
的值.
问题2.过抛物线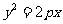 (
(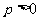 )的焦点作一条直线交抛物线于
)的焦点作一条直线交抛物线于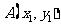 、
、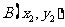 ,
,
两点,设直线的倾斜角为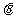 .求证:
.求证: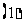
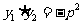 ;
;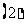
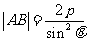
问题3.( 湖北)直线
湖北)直线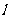 :
: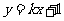 与双曲线
与双曲线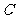 :
: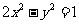 的右支交于不同的两点
的右支交于不同的两点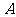 、
、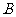 .(Ⅰ)求实数
.(Ⅰ)求实数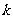 的取值范围;(Ⅱ)是否存在实数
的取值范围;(Ⅱ)是否存在实数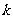 ,使得以线段
,使得以线段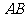 为直径的圆经过双曲线
为直径的圆经过双曲线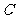 的右焦点
的右焦点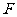 ?若存在,求出
?若存在,求出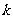 的值;若不存在,说明理由.
的值;若不存在,说明理由.
问题4. ( 天津质检)已知中心在原点,焦点在
天津质检)已知中心在原点,焦点在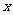 轴上的一个椭圆与圆
轴上的一个椭圆与圆
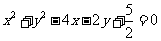 交于
交于 、
、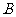 两点,
两点,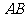 恰是该圆的直径,且
恰是该圆的直径,且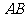 的斜率为
的斜率为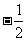 ,
,
求此椭圆的方程.
 对相交弦长问题及中点弦问题要正确运用“设而不求”,常结合韦达定理 .
对相交弦长问题及中点弦问题要正确运用“设而不求”,常结合韦达定理 .
 解决直线和圆锥曲线的位置关系问题时,经常转化为它们所对应的方程构成的方程组是否
解决直线和圆锥曲线的位置关系问题时,经常转化为它们所对应的方程构成的方程组是否
有解或解的个数问题.对于消元后的一元二次方程,必须讨论二次项的系数和判别式 ,注意直线与圆锥曲线相切必有一个公共点,对圆与椭圆来说反之亦对,但对双曲线和抛物线来说直线与其有一公共点,可能是相交的位置关系.有时借助图形的几何性质更为方便.
,注意直线与圆锥曲线相切必有一个公共点,对圆与椭圆来说反之亦对,但对双曲线和抛物线来说直线与其有一公共点,可能是相交的位置关系.有时借助图形的几何性质更为方便.
 涉及弦的中点问题,除利用韦达定理外,也可以运用“点差法”,但必须以直线与圆锥曲线相交为前提,否则不宜用此法.
涉及弦的中点问题,除利用韦达定理外,也可以运用“点差法”,但必须以直线与圆锥曲线相交为前提,否则不宜用此法.
 直线与圆锥曲线相交的弦长计算:
直线与圆锥曲线相交的弦长计算: 连结圆锥曲线上两点的线段称为圆锥曲线的弦;
连结圆锥曲线上两点的线段称为圆锥曲线的弦;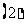 易求出弦端点坐标时用距离公式求弦长;
易求出弦端点坐标时用距离公式求弦长;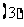 一般情况下,解由直线方程和圆锥曲线方程组成的方程组,得到关于
一般情况下,解由直线方程和圆锥曲线方程组成的方程组,得到关于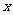 (或
(或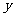 )的一元二次方程,利用方程组的解与端点坐标的关系,结合韦达定理得到弦长公式:
)的一元二次方程,利用方程组的解与端点坐标的关系,结合韦达定理得到弦长公式:
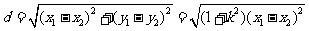 =
=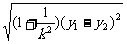 .
.
焦点弦的长也可以直接利用焦半径公式处理,可以使运算简化.焦点弦长: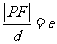
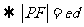 (点
(点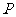 是圆锥曲线上的任意一点,
是圆锥曲线上的任意一点,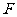 是焦点,
是焦点,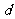 是
是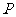 到相应于焦点
到相应于焦点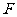 的
的
准线的距离, 是离心率)
是离心率)
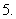 涉及垂直关系问题,一般是利用斜率公式及韦达定理求解,设
涉及垂直关系问题,一般是利用斜率公式及韦达定理求解,设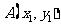 、
、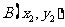 ,
,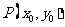 是直线与圆锥曲线的两个交点,
是直线与圆锥曲线的两个交点,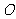 为坐标原点,则
为坐标原点,则
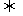
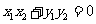 ,
,
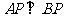
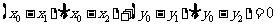
 解析几何解题的基本方法:数形结合法,以形助数,用数定形.常用此法简化运算.
解析几何解题的基本方法:数形结合法,以形助数,用数定形.常用此法简化运算.
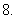 (
(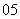 上海)过抛物线
上海)过抛物线 的焦点作一条直线与抛物线相交于
的焦点作一条直线与抛物线相交于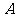 、
、 两点,它们的横坐标之和等于
两点,它们的横坐标之和等于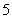 ,则这样的直线
,则这样的直线
 有且仅有一条
有且仅有一条  有且仅有两条
有且仅有两条  有无穷多条
有无穷多条  不存在
不存在
 (
( 陕西)抛物线
陕西)抛物线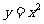 的准线方程是( )
的准线方程是( )

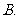

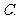

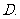

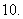 (
( 上海)已知双曲线
上海)已知双曲线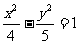 ,则以双曲线中心为焦点,以双曲线左焦点为顶点的抛物线方程为
,则以双曲线中心为焦点,以双曲线左焦点为顶点的抛物线方程为
 (
( 全国Ⅰ)抛物线
全国Ⅰ)抛物线 上的点到直线
上的点到直线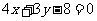 距离的最小值是
距离的最小值是
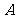
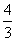
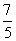
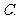
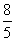
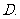
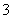
 (
( 山东)设
山东)设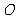 是坐标原点,
是坐标原点,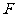 是抛物线
是抛物线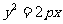
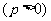 的焦点,
的焦点,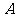 是抛物线
是抛物线
上的一点,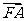 与
与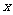 轴正向的夹角为
轴正向的夹角为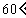 ,则
,则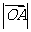 为
为
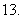 (
(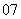 江西文)连接抛物线
江西文)连接抛物线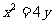 的焦点
的焦点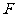 与点
与点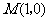 所得的线段与抛物线交于点
所得的线段与抛物线交于点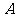 ,设点
,设点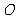 为坐标原点,则
为坐标原点,则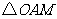 的面积为
的面积为



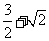
 (
( 全国Ⅱ)设
全国Ⅱ)设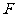 为抛物线
为抛物线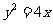 的焦点,
的焦点,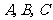 为该抛物线上三点,
为该抛物线上三点,
若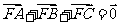 ,则
,则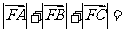
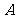
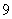
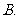

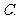
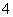
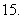 (
( 四川)已知抛物线
四川)已知抛物线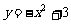 上存在关于直线
上存在关于直线 对称的相异两点
对称的相异两点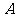 、
、 ,
,
则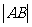 等于
等于 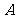
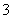
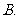
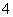
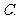
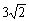
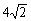
 (
( 全国Ⅰ)抛物线
全国Ⅰ)抛物线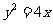 的焦点为
的焦点为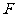 ,准线为
,准线为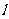 ,经过
,经过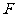 且斜率为
且斜率为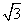 的直线与抛物线在
的直线与抛物线在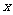 轴上方的部分相交于点
轴上方的部分相交于点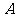 ,
,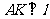 ,垂足为
,垂足为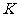 ,则
,则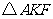 的面积是
的面积是
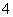
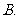

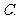
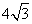
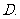
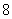
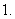 点
点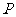
 在抛物线
在抛物线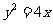 上,则
上,则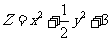 的最小值是
的最小值是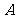
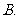
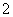
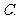
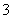
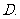
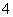
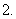 已知点
已知点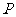 在抛物线
在抛物线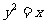 上,点
上,点 在圆
在圆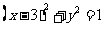 上,则
上,则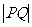 的最小值是
的最小值是
 (
( 届四川叙永一中阶段测试)过定点
届四川叙永一中阶段测试)过定点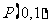 ,且与抛物线
,且与抛物线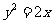 只有一个公共点的直线方程为
只有一个公共点的直线方程为
 抛物线
抛物线 的弦
的弦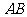 垂直于
垂直于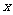 轴,若
轴,若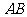 的长为
的长为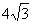 ,则焦点到
,则焦点到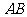 的距离是
的距离是
 斜率为
斜率为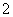 的直线被抛物线
的直线被抛物线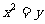 所截得线段中点的轨迹方程是
所截得线段中点的轨迹方程是
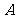
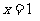
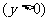
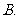
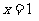
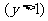
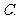

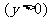
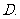

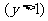
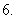 设抛物线
设抛物线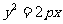
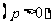 的焦点为
的焦点为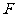 ,经过点
,经过点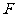 的直线交抛物线于
的直线交抛物线于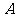 、
、 两点,点
两点,点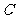 在抛物线的准线上,且
在抛物线的准线上,且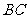 ∥
∥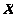 轴.证明直线
轴.证明直线 经过原点
经过原点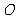
 (
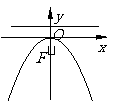
( 届高三贵州绥阳中学第四次月考)如图,过抛物线
届高三贵州绥阳中学第四次月考)如图,过抛物线
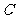 :
: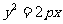
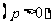 的焦点
的焦点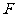 的直线
的直线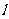 与该抛物线交于
与该抛物线交于
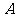 、
、 两点,若以线段
两点,若以线段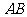 为直径的圆
为直径的圆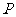 与该抛物线的
与该抛物线的
准线切于点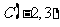 .
.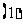 求抛物线
求抛物线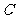 的方程;
的方程;
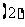 求圆
求圆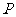 的方程.
的方程.
问题1.求满足下列条件的抛物线的标准方程,并求对应抛物线的准线方程:
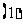 过点
过点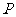
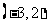 ;
;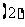 焦点在直线
焦点在直线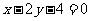 上;
上;
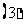 顶点在原点,对称轴为
顶点在原点,对称轴为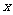 轴,抛物线上的点
轴,抛物线上的点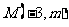 到焦点的距离等于
到焦点的距离等于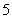 ;
;
 顶点在原点,对称轴为
顶点在原点,对称轴为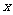 轴且截直线
轴且截直线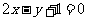 所得弦长为
所得弦长为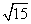 .
.
问题2. 在抛物线
在抛物线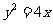 上找一点
上找一点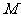 ,使
,使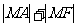 最小,其中
最小,其中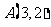 ,
,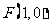 ,求
,求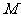 点的坐标及此时的最小值;
点的坐标及此时的最小值;
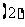 已知抛物线
已知抛物线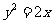 和定点
和定点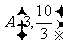 ,抛物线上有一动点
,抛物线上有一动点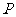 ,
,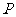 到点
到点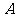 的距离为
的距离为 ,
,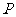 到抛物线准线的距离为
到抛物线准线的距离为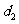 ,求
,求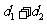 的最小值及此时
的最小值及此时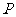 点的坐标.
点的坐标.
问题3. (
( 全国Ⅱ)抛物线
全国Ⅱ)抛物线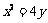 上一点
上一点 的纵坐标为
的纵坐标为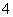 ,则点
,则点 与抛物线
与抛物线
焦点的距离为 
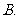
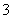
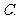
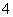
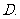
 (
( 海南)已知抛物线
海南)已知抛物线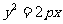
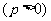 的焦点为
的焦点为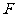 ,点
,点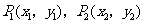 ,
,
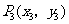 在抛物线上,且
在抛物线上,且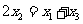 , 则有
, 则有
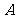
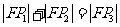
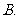
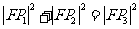
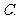
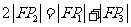
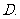
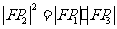
 定长为
定长为 的线段
的线段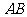 的端点
的端点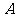 、
、 在抛物线
在抛物线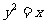 上移动,求线段
上移动,求线段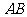 的中点
的中点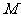 到
到
 轴距离的最小值.
轴距离的最小值.
 (
( 全国Ⅰ)抛物线
全国Ⅰ)抛物线 的点到直线
的点到直线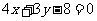 距离的最小值是
距离的最小值是
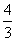
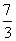
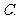
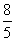
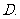
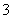
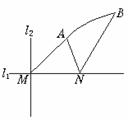
问题4.(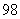 全国)直线
全国)直线 和
和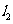 相交于点
相交于点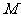 ,
,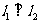 ,点
,点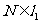 .以
.以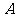 、
、 为端点的曲线段
为端点的曲线段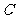 上的任一点到
上的任一点到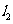 的距离与到点
的距离与到点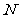 的距离相等.若
的距离相等.若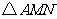 为锐角三角形,
为锐角三角形,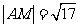 ,
,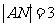 ,且
,且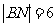 .建立适当的坐标系,求曲线段
.建立适当的坐标系,求曲线段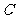 的方程.
的方程.
问题5.(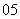 全国Ⅲ) 设
全国Ⅲ) 设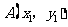 ,
,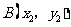 两点在抛物线
两点在抛物线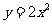 上,
上,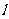 是
是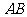 的垂直平分线。(Ⅰ)当且仅当
的垂直平分线。(Ⅰ)当且仅当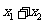 取何值时,直线
取何值时,直线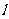 经过抛物线的焦点
经过抛物线的焦点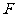 ?证明你的结论;(Ⅱ)当直线
?证明你的结论;(Ⅱ)当直线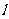 的斜率为
的斜率为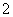 时,求
时,求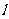 在
在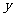 轴上截距的取值范围.
轴上截距的取值范围.
|
标准方程 |
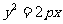 ( (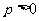 ) ) |
  ( (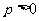 ) ) |
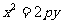 ( 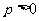 ) ) |
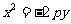 ( 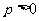 ) ) |
|
图形 |
 |
|
 |
 |
|
范围 |
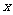 ≥ ≥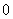 , , |
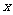 ≤ ≤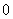 , , |
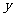 ≥ ≥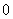 , ,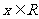 |
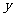 ≤ ≤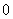 , ,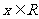 |
|
焦点 |
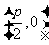 |
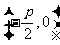 |
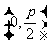 |
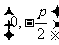 |
|
准线 |
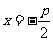 |
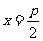 |
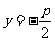 |
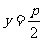 |
|
焦半径 |
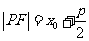 |
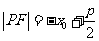 |
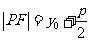 |
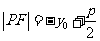 |
|
对称轴 |
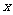 轴 轴 |
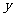 轴 轴 |
||
|
顶点 |
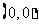 |
|||
|
离心率 |
 |
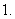 (课本
(课本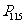 )
)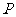 (
(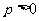 )的几何意义是抛物线的焦准距(焦点到准线的距离).
)的几何意义是抛物线的焦准距(焦点到准线的距离).
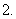 (课本
(课本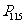 )抛物线的通径:通过焦点并且垂直于对称轴的直线与抛物线两交点之间的线段叫做抛物线的通径.通径的长为
)抛物线的通径:通过焦点并且垂直于对称轴的直线与抛物线两交点之间的线段叫做抛物线的通径.通径的长为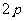 ,通径是过焦点最短的弦.
,通径是过焦点最短的弦.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com