
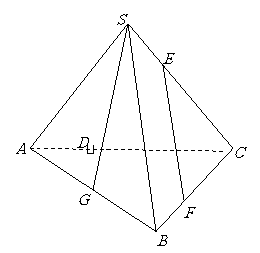
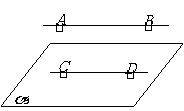
问题1.( 北京)如图,在底面为平行四边形的四棱锥
北京)如图,在底面为平行四边形的四棱锥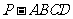 中,
中,
 ,
,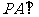 平面
平面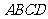 ,且
,且 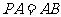 ,点
,点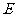 是
是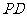 的中点.
的中点.
 略;
略;  求证:
求证: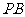 ∥平面
∥平面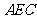 ;
;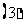 略.
略.
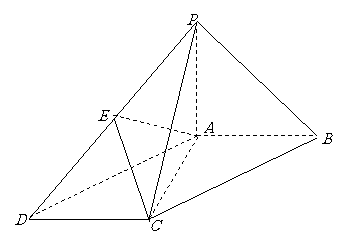
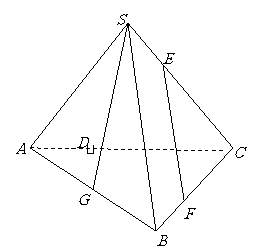 问题2.如图,在正三棱锥
问题2.如图,在正三棱锥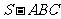 中,
中,
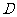 、
、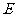 、
、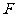 分别是棱
分别是棱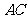 、
、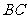 、
、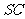 上的点,
上的点,
且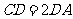 ,
,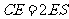 ,
,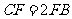 ,
,
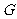 是
是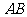 的中点.
的中点.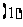 求证:平面
求证:平面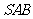 ∥平面
∥平面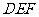 ;
;
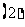 求证:
求证: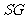 ∥平面
∥平面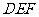
 (三)走向高考:
(三)走向高考:
 (
(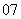 全国Ⅱ)如图,在四棱锥
全国Ⅱ)如图,在四棱锥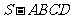 中,
中,
底面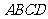 为正方形,侧棱
为正方形,侧棱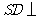 底面
底面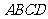 ,
,
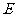 、
、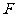 分别为
分别为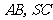 的中点.
的中点.
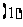 证明
证明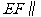 平面
平面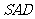 ;
;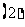 略.
略.
 线面平行的证明
线面平行的证明 判定定理:如果平面外一条直线与这个平面内一条直线平行,那么这条直线与这个平面平行;
判定定理:如果平面外一条直线与这个平面内一条直线平行,那么这条直线与这个平面平行; 两平面平行的性质定理:
两平面平行的性质定理: ∥
∥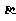 ,
,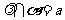 ,
,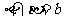

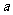 ∥
∥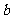 .
.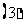 向量法. 方法1;
向量法. 方法1;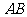 ∥
∥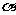
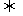
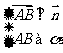
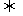
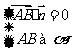
 方法2;
方法2;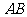 ∥
∥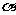
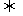
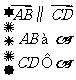
方法3;证明直线的方向向量与平面的两不共线向量是共面向量,
即利用平面向量基本定理进行证明.如图,
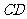 ∥
∥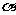
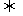
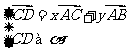 (其中
(其中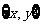 唯一且有序)
唯一且有序)
 面面平行的证明:
面面平行的证明: 判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.
判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.  垂直于同一条直线的两个平面平行;
垂直于同一条直线的两个平面平行; 平行于同一个平面的两个平面平行.
平行于同一个平面的两个平面平行. 设
设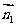 、
、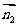 分别是平面
分别是平面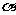 、
、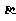 的法向量,若
的法向量,若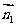 ∥
∥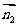 ,则
,则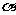 ∥
∥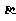
 (
( 海南)已知命题
海南)已知命题 :
: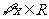 ,
,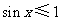 ,则( )
,则( )
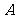
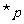 :
: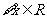 ,
,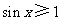
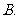
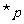 :
: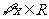 ,
,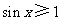
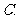
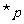 :
: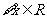 ,
,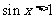
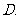
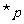 :
: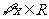 ,
,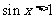
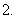 (
(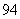 上海)某个命题与正整数
上海)某个命题与正整数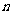 有关,若
有关,若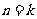
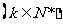 时该命题成立,那么可推得当
时该命题成立,那么可推得当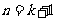 时该命题也成立,现已知当
时该命题也成立,现已知当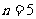 时该命题不成立,那么可推得( )
时该命题不成立,那么可推得( )
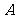 当
当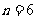 时该命题不成立
时该命题不成立 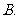 当
当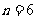 时该命题成立
时该命题成立
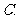 当
当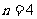 时该命题不成立
时该命题不成立  当
当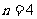 时该命题成立
时该命题成立
 (
(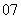 重庆)命题“若
重庆)命题“若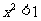 ,则
,则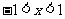 ”的逆否命题是( )
”的逆否命题是( )
 若
若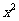 ≥
≥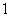 ,则
,则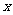 ≥
≥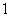 或
或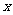 ≤
≤
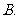 若
若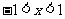 ,则
,则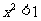
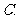 若
若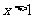 或
或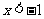 ,则
,则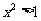
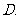 若
若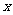 ≥
≥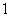 或
或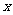 ≤
≤ ,则
,则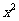 ≥
≥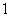
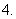 (
(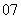 山东)命题“对任意的
山东)命题“对任意的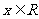 ,
,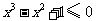 ”的否定是( )
”的否定是( )
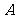 不存在
不存在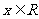 ,
,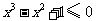 ;
; 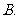 存在
存在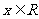 ,
,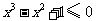 ;
;
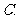 存在
存在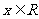 ,
,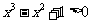 ;
;  对任意的
对任意的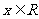 ,
,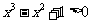
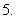 设命题
设命题 :函数
:函数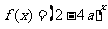 是
是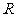 上的减函数,命题
上的减函数,命题 :函数
:函数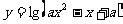 的定义域为
的定义域为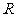 ,如果“
,如果“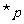 或
或 ”为假命题,求实数的
”为假命题,求实数的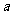 取值范围。
取值范围。
 (
(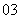 全国)已知
全国)已知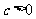 设
设 :函数
:函数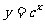 在
在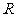 上单调递减.
上单调递减. :不等式
:不等式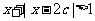
的解集为 ,如果
,如果 和
和 有且仅有一个正确,求
有且仅有一个正确,求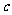 的取值范围.
的取值范围.
 对于命题“正方形的四个内角相等”,下面判断正确的是
对于命题“正方形的四个内角相等”,下面判断正确的是
 所给命题为假
所给命题为假  它的逆否命题为真
它的逆否命题为真  它的逆命题为真
它的逆命题为真 它的否命题为真
它的否命题为真
 若命题“
若命题“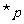 ”与命题“
”与命题“ 或
或 ”都是真命题,那么
”都是真命题,那么
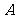 命题
命题 与命题
与命题 的真值相同
的真值相同 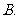 命题
命题 一定是真命题
一定是真命题
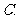 命题
命题 与命题
与命题 的真值不同
的真值不同 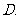 命题
命题 一定是假命题
一定是假命题
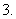 有下列四个命题:①“若
有下列四个命题:①“若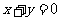 则
则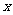 、
、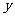 互为相反数”的逆命题;②“全等三角形
互为相反数”的逆命题;②“全等三角形
的面积相等”的否命题;③“若 ≤
≤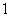 ,则
,则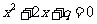 有实根”的逆否命题;
有实根”的逆否命题;
④“不等边三角形的三个内角相等”逆命题。其中真命题为
 ①②
①②
 ②③
②③
 ①③
①③
 ③④
③④
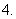 语句
语句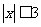 或
或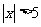 的否定是
的否定是
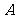
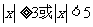
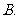
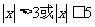
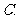
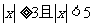
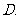
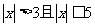
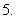 若命题
若命题 :
: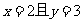 ,则
,则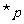 是
是
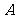
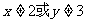
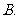
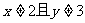
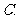
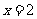 或
或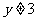
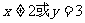
 一个命题与它的逆命题、否命题、逆否命题这四个命题中
一个命题与它的逆命题、否命题、逆否命题这四个命题中
 真命题的个数一定是奇数
真命题的个数一定是奇数
 真命题的个数一定是偶数
真命题的个数一定是偶数
 真命题的个数可能是奇数也可能是偶数
真命题的个数可能是奇数也可能是偶数  上述判断都不正确
上述判断都不正确
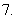 若
若 是真命题,
是真命题, 是假命题。以下四个命题:①
是假命题。以下四个命题:① 且
且 ;②
;② 或
或 ;③非
;③非 ;④非
;④非 .其中假命的个数是
.其中假命的个数是 
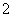
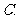
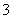
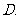
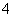
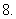 命题“若
命题“若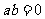 ,则
,则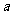 、
、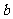 中至少有一个为零”的逆否命题为___________
中至少有一个为零”的逆否命题为___________
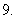 命题“存在
命题“存在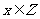 ,使
,使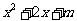 ≤
≤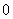 ”的否定是( )
”的否定是( )
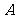 存在
存在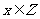 使
使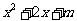

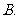 不存在
不存在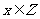 使
使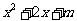

 对任意
对任意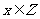 使
使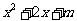 ≤
≤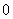
 对任意
对任意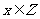 使
使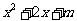

 (
( 重庆理)一元二次方程
重庆理)一元二次方程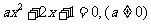 有一个正根和一个负根的充分
有一个正根和一个负根的充分
不必要条件是( )
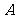
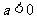
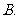
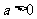
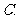
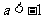
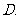
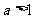
 (
( 成都统考)若
成都统考)若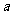 、
、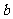 、
、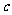 均为实数,且
均为实数,且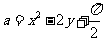 ,
,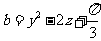 ,
,
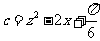 ,求证:
,求证: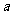 、
、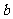 、
、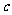 中至少有一个大于
中至少有一个大于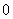
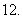 证明:“若
证明:“若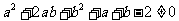 则
则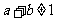 ”为真命题
”为真命题
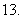 用反证法证明:不存在整数
用反证法证明:不存在整数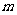 、
、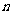 ,使得
,使得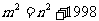
 命题“若
命题“若 不正确,则
不正确,则 不正确”的逆命题的等价命题是( )
不正确”的逆命题的等价命题是( )
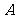 若
若 不正确,则
不正确,则 不正确
不正确 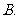 若
若 不正确,则
不正确,则 正确
正确
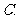 若
若 正确,则
正确,则 不正确
不正确
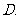 若
若 正确,则
正确,则 正确
正确
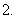 若命题
若命题 的逆命题是
的逆命题是 ,命题
,命题 的否命题为
的否命题为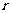 ,则以下判断正确的是
,则以下判断正确的是
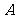
 是
是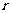 的逆命题
的逆命题 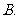
 是
是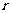 的否命题
的否命题 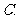
 是
是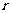 的逆否命题
的逆否命题 
 是
是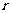 的关系不定
的关系不定
 (
( 郴州模拟)若
郴州模拟)若 且
且 ”与“
”与“ 或
或 ”均为假命题,则( )
”均为假命题,则( )
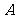 命题“
命题“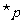 ”与“
”与“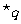 ”的真值不同
”的真值不同 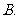 命题“
命题“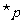 ”与“
”与“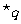 ”至少有一个是假命题
”至少有一个是假命题
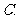 命题“
命题“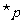 ”与“
”与“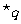 ”的真值相同
”的真值相同  命题“
命题“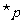 ”与“
”与“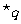 ”都是真命题
”都是真命题
问题1.
分别指出由下列命题构成的“ 或
或 ”、“
”、“ 且
且 ”、“非
”、“非 ”形式的复合命题的真假:
”形式的复合命题的真假:
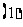
 :
: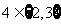 ,
, :
: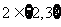 ;
;
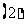
 :
: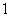 是奇数,
是奇数, :
: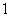 是质数;
是质数;
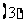
 :
: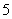 ≤
≤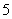 ,
, :
: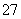 不是质数;
不是质数;
问题2.
①分别写出命题“若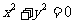 ,则
,则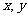 全为零”的逆命题、否命题和逆否命题.
全为零”的逆命题、否命题和逆否命题.
②( 江苏)命题“若
江苏)命题“若 ,则
,则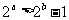 ”的否命题为
”的否命题为
该命题的否定是 (编者自拟)
问题3.命题“若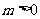 ,则
,则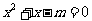 有实根”的逆否命题是真命题吗?证明你的结论.
有实根”的逆否命题是真命题吗?证明你的结论.
问题4. 已知命题 :方程
:方程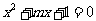 有两个不等的负实根,命题
有两个不等的负实根,命题 :方程
:方程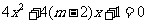 无实根;若
无实根;若 或
或 为真,
为真, 且
且 为假,求实数
为假,求实数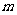 的取值范围.
的取值范围.
问题5.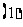 用反证法证明命题:若整数系数一元二次方程:
用反证法证明命题:若整数系数一元二次方程: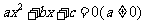 有有理根,那么
有有理根,那么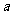 、
、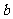 、
、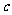 中至少有一个是偶数,下列假设中正确的是
中至少有一个是偶数,下列假设中正确的是
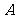 假设
假设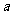 、
、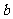 、
、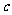 都是偶数
都是偶数
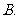 假设
假设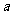 、
、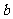 、
、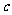 都不是偶数
都不是偶数
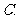 假设
假设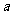 、
、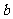 、
、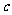 至多有一个是偶数
至多有一个是偶数 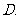 假设
假设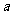 、
、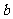 、
、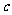 至多有两个是偶数
至多有两个是偶数
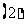 已知函数
已知函数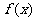 对其定义域内的任意两个数
对其定义域内的任意两个数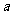 、
、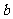 ,当
,当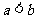 时,都有
时,都有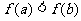 ,证明:
,证明: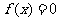 至多有一个实根.
至多有一个实根.
 逻辑联结词“或”“且”“非”与集合中的并集、交集、补集有着密切的关系,解题时注意类比;
逻辑联结词“或”“且”“非”与集合中的并集、交集、补集有着密切的关系,解题时注意类比;
 通常复合命题“
通常复合命题“ 或
或 ”的否定为“
”的否定为“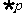 且
且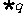 ”、“
”、“ 且
且 ”的否定为“
”的否定为“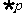 或
或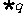 ”、“全为”的否定是“不全为”、“都是”的否定为“不都是”等等;
”、“全为”的否定是“不全为”、“都是”的否定为“不都是”等等;
 有时一个命题的叙述方式比较的简略,此时应先分清条件和结论,该写成“若
有时一个命题的叙述方式比较的简略,此时应先分清条件和结论,该写成“若 ,则
,则 ”的形式;
”的形式;
 反证法中出现怎样的矛盾,要在解题的过程中随时审视推出的结论是否与题设、定义、定理、公理、公式、法则等矛盾,甚至自相矛盾.
反证法中出现怎样的矛盾,要在解题的过程中随时审视推出的结论是否与题设、定义、定理、公理、公式、法则等矛盾,甚至自相矛盾.
 理解由“或”“且”“非”将简单命题构成的复合命题;
理解由“或”“且”“非”将简单命题构成的复合命题;
 由真值表判断复合命题的真假;
由真值表判断复合命题的真假;
 四种命题间的关系.
四种命题间的关系.
 (
(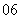 北京)平面
北京)平面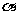 的斜线
的斜线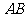 交
交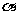 于点
于点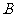 ,过定点
,过定点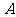 的动直线
的动直线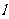 与
与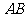 垂直,且交
垂直,且交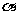
于点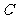 ,则动点
,则动点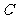 的轨迹是
的轨迹是 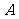 一条直线
一条直线  一个圆
一个圆  一个椭圆
一个椭圆  双曲线的一支
双曲线的一支
 (
( 北京文)设
北京文)设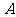 、
、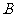 、
、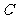 、
、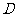 是空间四个不同的点,在下列命题中,不正确的是
是空间四个不同的点,在下列命题中,不正确的是
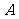 若
若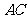 与
与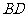 共面,则
共面,则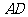 与
与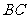 共面
共面
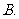 若
若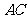 与
与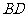 是异面直线,则
是异面直线,则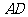 与
与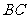 是异面直线
是异面直线
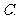 若
若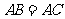 ,
,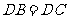 ,则
,则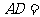
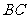
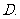 若
若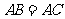 ,
,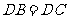 ,则
,则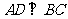
 (
( 重庆)对于任意的直线
重庆)对于任意的直线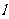 与平面
与平面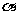 ,在平面
,在平面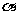 内必有直线
内必有直线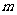 ,使
,使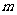 与
与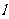
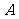 平行
平行
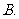 相交
相交
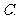 垂直
垂直
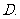 互为异面直线
互为异面直线
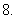 (
( 全国Ⅰ)在正方形
全国Ⅰ)在正方形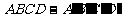 中,过对角线
中,过对角线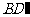 的一个平面交
的一个平面交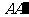 于
于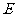 ,交
,交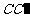 于
于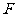 ,则
,则
①
四边形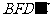 一定是平行四边形;
一定是平行四边形;
②
四边形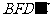 有可能是正方形
有可能是正方形
③
四边形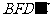 在底面
在底面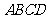 内的投影一定是正方形
内的投影一定是正方形
④
四边形 有可能垂直于平面
有可能垂直于平面
以上结论正确的为 (写出所有正确结论的编号)
 (
( 浙江)若
浙江)若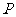 是两条异面直线
是两条异面直线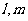 外的任意一点,则
外的任意一点,则
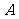 过点
过点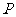 有且仅有一条直线与
有且仅有一条直线与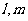 都平行
都平行 过点
过点 有且仅有一条直线与
有且仅有一条直线与 都垂直
都垂直
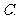 过点
过点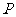 有且仅有一条直线与
有且仅有一条直线与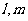 都相交
都相交 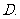 过点
过点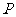 有且仅有一条直线与
有且仅有一条直线与 都异面
都异面
 (
(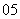 天津)如图,
天津)如图,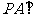 平面
平面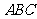 ,
,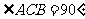 ,
,
且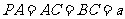 ,则异面直线
,则异面直线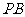 与
与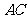 所成角
所成角
的余弦值为
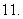 (
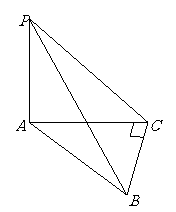
(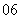 江西文)如图,已知三棱锥
江西文)如图,已知三棱锥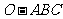 的侧棱
的侧棱
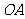 、
、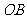 、
、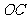 两两垂直,且
两两垂直,且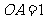 ,
,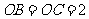 ,
,
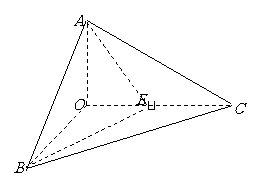
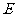 是
是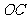 的中点.
的中点. 略;
略;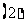 求异面直线
求异面直线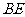 与
与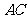 所成的角;
所成的角;
 略.
略.
问题1. (
( 上海)若空间中有四个点,则“这四个点中有三点在同一直线上”
上海)若空间中有四个点,则“这四个点中有三点在同一直线上”
是“这四个点在同一平面上”的
 充分非必要条件;
充分非必要条件;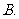 必要非充分条件;
必要非充分条件;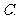 充要条件;
充要条件;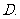 非充分非必要条件.
非充分非必要条件.
 (
( 全国Ⅲ)不共面的四个定点到平面
全国Ⅲ)不共面的四个定点到平面 的距离都相等,这样的平面
的距离都相等,这样的平面 共有
共有
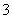 个
个
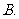
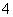 个
个
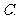
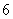 个
个
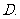
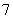 个
个
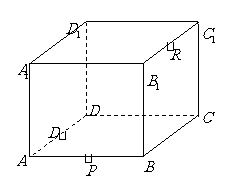
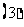 (
( 全国Ⅱ)正方体
全国Ⅱ)正方体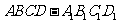 中,
中,
 、
、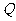 、
、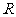 分别是
分别是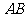 、
、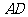 、
、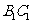 的中点.
的中点.
那么,正方体的过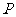 、
、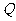 、
、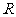 的截面图形是
的截面图形是
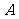 三角形
三角形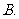 四边形
四边形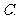 五边形
五边形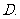 六边形
六边形
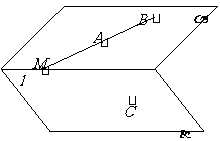
 如图,
如图, ,
, 、
、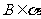 ,
,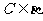 ,
,
且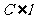 ,直线
,直线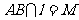 ,过
,过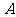 、
、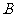 、
、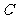 三点
三点
的平面记作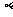 ,则
,则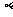 与
与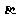 的交线必通过
的交线必通过
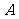 点
点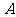 ;
;
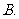 点
点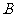 ;
;
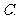 点
点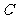 但不通过点
但不通过点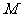 ;
; 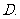 点
点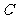 和点
和点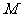

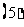 (
( 江苏)如图,已知
江苏)如图,已知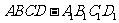 是棱长
是棱长
为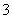 的正方体,点
的正方体,点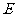 在
在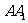 上,点
上,点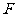 在
在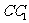 上,
上,
且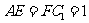 .
. 求证:
求证: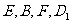 四点共面;(
四点共面;(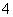 分)
分)
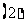 略;
略;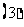 略.
略.
问题2.(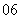 全国Ⅱ)如图,在直三棱柱
全国Ⅱ)如图,在直三棱柱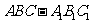 中,
中,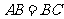 ,
,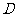 、
、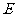 分别
分别
为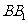 、
、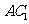 的中点.
的中点. 证明:
证明: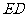 为异面直线
为异面直线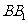 与
与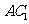 的公垂线;
的公垂线;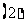 略.
略.
( 要求用传统方法和向量法,注意书写的规范性)
 证明:方法
证明:方法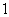 (用传统方法):
(用传统方法):
方法 (用向量法):
(用向量法):

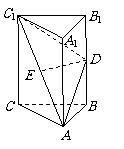
问题3.如图,在正方体 中,
中,
棱长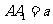 ,
, 求证:
求证: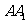 与
与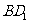 是异面直线;
是异面直线;
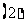 求
求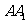 于
于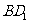 间的距离.
间的距离.
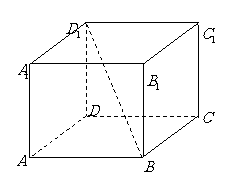
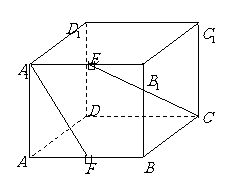
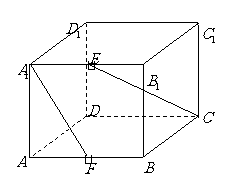
问题4.(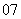 上海春)在棱长为
上海春)在棱长为 的正方体
的正方体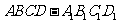 中,
中,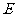 、
、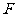 分别是
分别是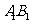 、
、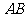 的中点,求异面直线
的中点,求异面直线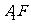 与
与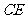 所成的角( 要求用传统方法和向量法,注意书写的规范性).
所成的角( 要求用传统方法和向量法,注意书写的规范性).
解法1(传统方法):
解法2(向量法):
 (三)课后作业:
(三)课后作业:
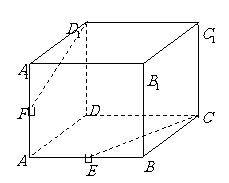
 如图,在正方体
如图,在正方体 中,
中, 、
、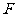 分别
分别
是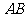 、
、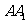 的中点,求证:
的中点,求证:
①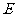 、
、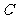 、
、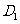 、
、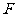 四点共面;
四点共面;
②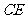 、
、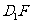 、
、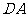 三点共线.
三点共线.
 角
角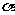 与
与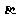 的两边分别平行,当
的两边分别平行,当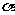
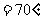 时,
时, 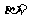
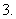 已知
已知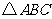 的直观图是边长为
的直观图是边长为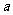 的等边
的等边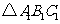 ,那么
,那么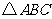 的面积为
的面积为

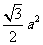
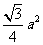
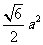
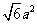
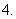 如图,在空间四边形
如图,在空间四边形 中,已知
中,已知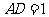 ,
,
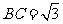 ,且
,且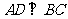 ,对角线
,对角线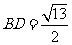 ,
,
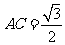 ,求
,求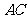 与
与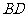 所成的角.
所成的角.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com