
7.(2008广州一模理)在区间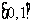 上任取两个数
上任取两个数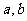 ,方程
,方程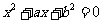
的两根均为实数的概率为( )
A.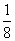 B.
B.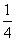 C.
C.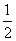 D.
D.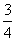
6.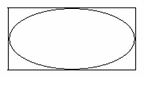 (2008佛山一模理)如图,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,数得落在椭圆外的黄豆数为96颗,以此实验数据为依据可以估计出椭圆的面积约为( )
(2008佛山一模理)如图,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,数得落在椭圆外的黄豆数为96颗,以此实验数据为依据可以估计出椭圆的面积约为( )
A.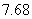 B.
B.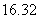 C.
C.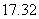 D.
D.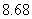
5. (2007韶关二模文) 一个停车场有3个并排的车位,分别停放着“红旗”,“捷达”,“桑塔纳”轿车各一辆,则“捷达””车停在“桑塔纳”车的右边的概率和“红旗”车停在最左边的概率分别是( )
A. 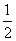 ,
,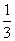
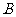 .
. 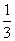 ,
,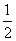
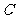 .
. 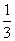 ,
,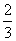
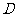 .
. 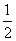 ,
,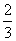
4.(2007韶关一模文)有3张奖券,其中2张可中奖,现3个人按顺序依次从中抽一张,小明最后抽,
则他抽到中奖券的概率是( )
(A)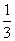 (B)
(B)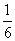 (C)
(C)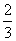 (D)
(D)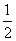
3.( 2005年广东)先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有1,2,3,4,5,6),
骰子朝上的面的点数分别为x,y,则使
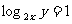 的概率为( )
的概率为( )
A.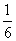 B.
B.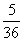 C.
C.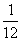 D.
D.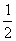
2.(2008惠州调研二理)方程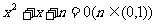 有实根的概率为(
).
有实根的概率为(
).
A、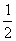 B、
B、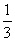 C、
C、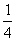 D、
D、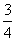
1.(2008辽宁文、理) 4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为( )
A.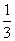 B.
B.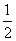 C.
C.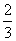 D.
D.
 (
( 全国Ⅱ)函数
全国Ⅱ)函数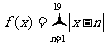 的最小值为
的最小值为
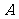
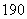
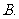
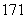
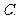
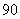
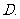
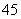
 (
( 湖北)函数
湖北)函数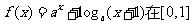 上的最大值与最小值之和为
上的最大值与最小值之和为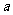 ,
,
则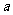 的值为
的值为 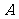
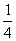
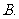
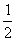
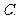
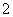
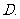
 (
(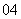 湖北文)已知
湖北文)已知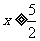 ,则
,则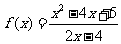 有
有
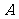 最大值
最大值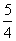
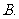 最小值
最小值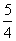
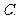 最大值
最大值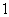
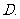 最小值
最小值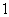
 (
( 重庆文)函数
重庆文)函数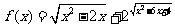 的最小值为
的最小值为
 (
( 安徽)设
安徽)设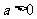 ,对于函数
,对于函数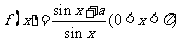 ,下列结论正确的是
,下列结论正确的是
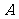 有最大值而无最小值
有最大值而无最小值 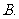 有最小值而无最大值
有最小值而无最大值
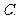 有最大值且有最小值
有最大值且有最小值 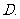 既无最大值又无最小值
既无最大值又无最小值
 (
( 陕西文)函数
陕西文)函数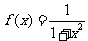
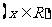 的值域是
的值域是
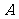
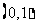
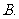
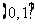
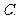
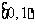
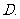
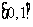
 (
( 上海文)若曲线
上海文)若曲线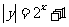 与直线
与直线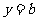 没有公共点,则
没有公共点,则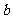 的取值范围为
的取值范围为
 (
(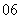 福建文)已知
福建文)已知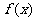 是二次函数,不等式
是二次函数,不等式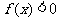 的解集是
的解集是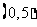 ,且
,且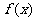 在区间
在区间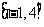 上的最大值是
上的最大值是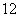 .
.
(Ⅰ)求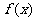 的解析式;
的解析式;
(Ⅱ)是否存在在自然数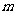 ,使得方程
,使得方程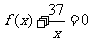 在区间
在区间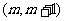 内有且只有两个不等的实数根?若存在,求出所有
内有且只有两个不等的实数根?若存在,求出所有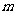 的值;若不存在,说明理由.
的值;若不存在,说明理由.
 求下列函数的值域:
求下列函数的值域:
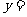
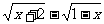 (
(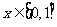 );
);
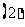
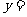
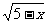 +
+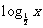 ;
;

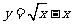
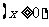 ;
;
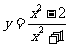 ;
;
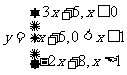
 函数
函数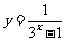 的值域是
的值域是

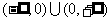
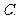
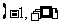
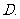
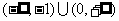
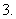 已知函数
已知函数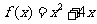 ,则
,则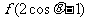 的值域是
的值域是
 函数
函数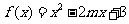 在区间
在区间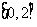 上的值域为
上的值域为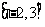 ,则
,则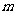 的值为( )
的值为( )
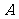
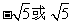
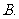
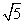 或
或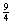
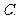
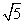
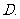
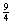
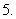 (
(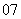 江苏通州一中质检)函数
江苏通州一中质检)函数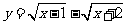 的最小值为
的最小值为
 (
( 江苏)已知函数
江苏)已知函数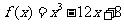 在区间
在区间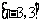 上的最大值与最小值分别为
上的最大值与最小值分别为
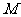 、
、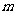 ,则
,则 _____.
_____.
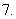 若函数
若函数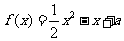 的定义域和值域均为
的定义域和值域均为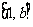
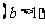 ,求
,求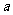 、
、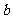 的值
的值
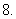 函数
函数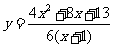
 的最小值是( )
的最小值是( )
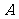
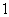
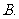
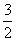
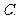
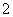
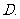
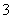
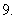 (
( 长春四市一模)函数
长春四市一模)函数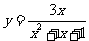
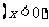 的值域是
的值域是
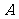
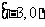
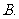
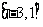
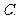

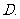
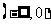
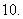 (
(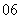 新海中学模拟)函数
新海中学模拟)函数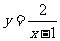 的定义域是
的定义域是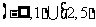 ,则其值域是
,则其值域是
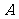
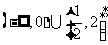
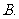
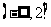
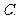
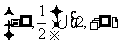
 求函数
求函数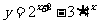
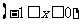 的值域
的值域
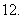 定义在
定义在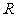 上的函数
上的函数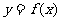 的值域为
的值域为 ,则函数
,则函数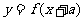 的值域为
的值域为
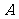

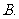

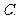

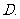
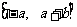
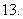 已知
已知
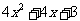
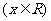 ,那么函数
,那么函数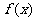 的最小值为
的最小值为
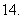 若
若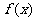 的值域为
的值域为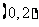 ,则
,则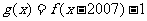 的值域为
的值域为
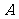
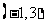
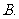
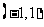
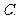
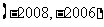
 以上都不对
以上都不对
 (
( 江西)设函数
江西)设函数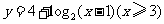 ,则其反函数的定义域为
,则其反函数的定义域为
 已知函数
已知函数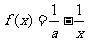
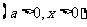 .
.
 若
若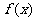 在
在 上的值域是
上的值域是 ,求
,求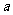 的取值范围,并求相应的
的取值范围,并求相应的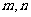 的值;
的值;
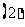 若
若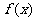 ≤
≤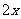 在
在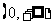 上恒成立,求
上恒成立,求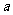 的取值范围
的取值范围
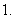 函数
函数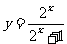 的值域为
的值域为
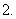 若函数
若函数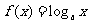 在
在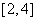 上的最大值与最小值之差为
上的最大值与最小值之差为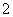 ,则
,则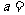
 已知
已知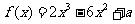 (
(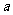 是常数),在
是常数),在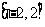 上有最大值
上有最大值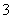 ,那么在
,那么在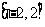 上的最小值是
上的最小值是 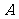

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com