
7.设抛物线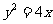 的过焦点的弦的两个端点为A、B,它们的坐标为
的过焦点的弦的两个端点为A、B,它们的坐标为 ,若
,若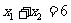 ,那么
,那么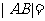 。
。
6.过定点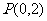 ,作直线
,作直线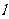 与曲线
与曲线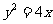 有且仅有1个公共点,则这样的直线
有且仅有1个公共点,则这样的直线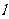 共有 条;
共有 条;
5.抛物线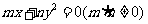 的顶点坐标是 ,焦点坐标是 ,准线方程是 ,离心率是 ,通径长 .
的顶点坐标是 ,焦点坐标是 ,准线方程是 ,离心率是 ,通径长 .
1(05上海)过抛物线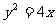 的焦点作一条直线与抛物线相交于A、B两点,它们的横坐标之和等于5,则这样的直线( )
的焦点作一条直线与抛物线相交于A、B两点,它们的横坐标之和等于5,则这样的直线( )
A.有且仅有一条 B.有且仅有两条 C.有无穷多条 D.不存在
2.(05江苏卷)抛物线y=4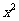 上的一点M到焦点的距离为1,则点M的纵坐标是( )
上的一点M到焦点的距离为1,则点M的纵坐标是( )
( A
) 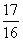 (
B )
(
B ) 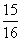 (
C )
(
C ) 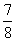 (
D ) 0
(
D ) 0
3方程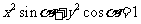 表示的曲线不可能是 (
)
表示的曲线不可能是 (
)
 直线
直线
 抛物线
抛物线
 圆
圆
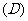 双曲线
双曲线
4以抛物线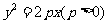 的焦半径
的焦半径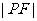 为直径的圆与
为直径的圆与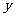 轴位置关系是( )
轴位置关系是( )
 相交
相交  相切
相切  相离
相离 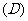 以上三种均有可能
以上三种均有可能
例1.抛物线以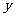 轴为准线,且过点
轴为准线,且过点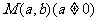 ,证明:不论
,证明:不论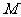 点在坐标平面内的位置如何变化,抛物线顶点的轨迹的离心率是定值.
点在坐标平面内的位置如何变化,抛物线顶点的轨迹的离心率是定值.
例2.已知抛物线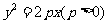 ,过动点
,过动点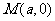 且斜率为
且斜率为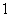 的直线
的直线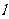 与该抛物线交于不同两点
与该抛物线交于不同两点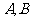 ,
,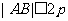 ,
,
(1)求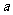 取值范围;
取值范围;
(2)若线段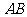 垂直平分线交
垂直平分线交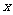 轴于点
轴于点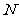 ,求
,求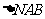 面积的最大值
面积的最大值
例3. 已知抛物线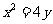 与圆
与圆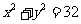 相交于
相交于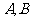 两点,圆与
两点,圆与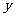 轴正半轴交于
轴正半轴交于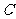 点,直线
点,直线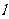 是圆的切线,交抛物线与
是圆的切线,交抛物线与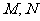 ,并且切点在
,并且切点在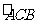 上.
上.
(1)求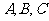 三点的坐标.(2)当
三点的坐标.(2)当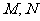 两点到抛物线焦点距离和最大时,求直线
两点到抛物线焦点距离和最大时,求直线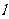 的方程.
的方程.
例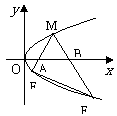 4(05江西卷)如图,M是抛物线上y2=x上的一点,动弦ME、MF分别交x轴于A、B两点,且MA=MB.
4(05江西卷)如图,M是抛物线上y2=x上的一点,动弦ME、MF分别交x轴于A、B两点,且MA=MB.
(1)若M为定点,证明:直线EF的斜率为定值;
(2)若M为动点,且∠EMF=90°,求△EMF的重心G的轨迹
4.抛物线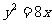 的焦点为
的焦点为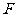 ,
,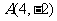 为一定点,在抛物线上找一点
为一定点,在抛物线上找一点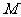 ,
,
当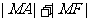 为最小时,则
为最小时,则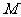 点的坐标
,当
点的坐标
,当 为最大时,则
为最大时,则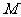 点的坐标
.
点的坐标
.
3.过点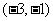 的抛物线的标准方程是
.焦点在
的抛物线的标准方程是
.焦点在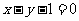 上的抛物线的标准方程是
.
上的抛物线的标准方程是
.
2.设抛物线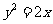 的焦点为
的焦点为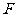 ,以
,以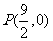 为圆心,
为圆心,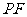 长为半径作一圆,与抛物线在
长为半径作一圆,与抛物线在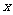 轴上方交于
轴上方交于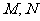 ,则
,则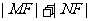 的值为 ( )
的值为 ( )
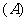 8
8 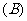 18
18 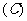
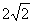
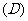 4
4
1.已知点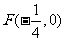 ,直线
,直线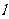 :
: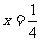 ,点
,点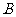 是直线
是直线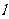 上的动点,若过
上的动点,若过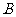 垂直于
垂直于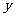 轴的直线与线段
轴的直线与线段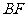 的垂直平分线交于点
的垂直平分线交于点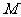 ,则点
,则点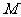 所在曲线是 ( )
所在曲线是 ( )
 圆
圆
 椭圆
椭圆  双曲线
双曲线  抛物线
抛物线
2.开口向右、向左、向上、向下的抛物线及其标准方程的异同点:
相同点:(1)原点在抛物线上;(2)对称轴为坐标轴;p值的意义表示焦点到准线的距离;(3)p>0为常数;(4)p值等于一次项系数绝对值的一半;(5)准线与对称轴垂直,垂足与焦点关于原点对称,它们与原点的距离等于一次项系数的绝对值的1/4,即2p/4=p/2.
不同点:
|
方程 |
对称轴 |
开口方向 |
焦点位置 |
|
y2=2px |
x轴 |
向右 |
x轴正半轴上 |
|
y2= -2px(p>0) |
x轴 |
向左 |
x轴负半轴上 |
|
x2=2py(p>0) |
y轴 |
向上 |
y轴正半轴上 |
|
x2= -2py(p>0) |
y轴 |
向下 |
y轴负半轴上 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com