
1.十字路口来往的车辆,如果不允许回头,则行车路线共有 ( ).
A.24种 B.16种 C.12种 D.10种
分类计数原理和分步计数原理
(1)分类计数原理(加法原理):
做一件事情,完成它可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法。那么完成这件事共有 N=m1+m2+…+mn 种不同的方法。
(2) 分步计数原理(乘法原理):
做一件事情,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事有 N=m1×m2×…×mn
种不同的方法。
13、设曲线C的方程为y=x3-x,将C沿x轴、y轴正向分别平移t、s个单位后得到曲线C1.
⑴求C1的方程;
⑵证明C、C1关于点 对称;
对称;
12、椭圆 上存在两个不同的点A、B关于直线y=4x+m对称,求实数m的取值范围.
上存在两个不同的点A、B关于直线y=4x+m对称,求实数m的取值范围.
11、在抛物线y2=2x上求一点P,使得P到直线x-y+3=0的距离最小.
10.已知抛物线 :
: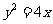 ,动直线
,动直线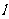 :
: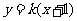 与抛物线
与抛物线 交于
交于 两点,
两点, 为原点,(1)求证:
为原点,(1)求证: 是定值;(2)求满足
是定值;(2)求满足 的点
的点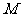 的轨迹方程.
的轨迹方程.
9.已知圆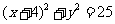 的圆心为
的圆心为 ,圆
,圆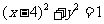 的圆心为
的圆心为 ,一动圆与这两个圆都相切,(1)求动圆圆心
,一动圆与这两个圆都相切,(1)求动圆圆心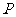 的轨迹方程;(2)若过点
的轨迹方程;(2)若过点 的直线与(1)中所求轨迹有两个交点
的直线与(1)中所求轨迹有两个交点 ,求
,求 的取值范围.
的取值范围.
8.设抛物线 :
: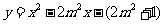
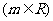 ,
,
(1)求证:抛物线 恒过
恒过 轴上一定点
轴上一定点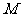 ;
;
(2)若抛物线与 轴的正半轴交于点
轴的正半轴交于点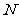 ,与
,与 轴交于点
轴交于点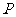 ,求证:
,求证: 的斜率为定值;
的斜率为定值;
(3)当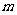 为何值时,
为何值时, 的面积最小?并求此最小值.
的面积最小?并求此最小值.
7.以 轴为准线的椭圆经过定点
轴为准线的椭圆经过定点 ,且离心率
,且离心率 ,则椭圆的左顶点的轨迹方程为
.
,则椭圆的左顶点的轨迹方程为
.
6. (05浙江) 过双曲线 (a>0,b>0)的左焦点且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于________.
(a>0,b>0)的左焦点且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com