
4.(2009·新郑调研)若f(x)=logax在[2,+∞)上恒有f(x)>1,则实数a的取值范围是 ( )
A.(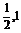 )?
B.(0,
)?
B.(0, )∪(1,2)
)∪(1,2)
?C.(1,2)
D. (0, )∪(2,+∞)
)∪(2,+∞)
答案?C?
3.已知log7[log3(log2x)]=0,那么x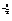 等于
( )
等于
( )
A.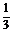 ?B.
?B.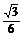 C.
C.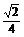 ? D.
? D.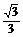
答案?C?
2.已知3a=5b=A,且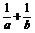 =2,则A的值是
( )
=2,则A的值是
( )
A.15
B.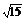 C.±
C.±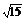 D.225
D.225
答案?B?
1.(2008·全国Ⅱ理,4)若x∈(e-1,1),a=lnx,b=2lnx,c=ln3x,则 ( )
A.a<b<c B.c<a<b C.b<a<c D.b<c<a
答案?C?
12.已知f(x)=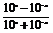 .
.
(1)判断函数奇偶性;
(2)证明:f(x)是定义域内的增函数;
(3)求f(x)的值域.
(1)解 ∵f(x)的定义域为R,
且f(-x)=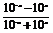 =-f(x),
=-f(x),
∴f(x)是奇函数.
(2)证明 方法一 f(x)=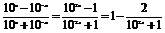 .
.
令x2>x1,则f(x2)-f(x1)
=(1-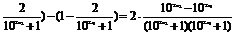
当x2>x1时,10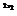 -10
-10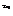 >0. 又∵10
>0. 又∵10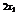 +1>0,10
+1>0,10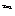 +1>0,
+1>0,
故当x2>x1时,f(x2)-f(x1)>0, 即f(x2)>f(x1).所以f(x)是增函数.
方法二 考虑复合函数的增减性.
由f(x)=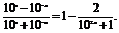 ∵y1=10x为增函数,
∵y1=10x为增函数,
∴y2=102x+1为增函数,y3=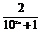 为减函数,
为减函数,
y4=-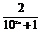 为增函数,
为增函数,
f(x)=1-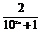 为增函数.
为增函数.
∴f(x)=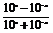 在定义域内是增函数.
在定义域内是增函数.
(3)解 方法一 令y=f(x),由y=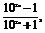 解得102x=
解得102x=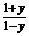 .
.
∵102x>0,∴-1<y<1.
即f(x)的值域为(-1,1).
方法二 ∵f(x)=1-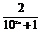 ,∵102x>0,∴102x+1>1.
,∵102x>0,∴102x+1>1.
∴0<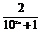 <2,∴-1<1-
<2,∴-1<1-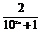 <1,即值域为(-1,1).
<1,即值域为(-1,1).
§2.7 对数与对数函数
 基础自测
基础自测
11.已知函数f(x)=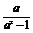 (ax-a-x) (a>0,且a≠1).
(ax-a-x) (a>0,且a≠1).
(1)判断f(x)的单调性;
(2)验证性质f(-x)=-f(x),当x∈(-1,1)时,并应用该性质求满足f(1-m)+f(1-m2)<0的实数m的范围.
解 (1)设x1<x2,x1-x2<0,1+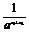 >0.
>0.
若a>1,则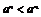 ,
,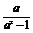 >0,
>0,
所以f(x1)-f(x2)=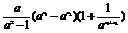 <0,
<0,
即f(x1)<f(x2),f(x)在(-∞,+∞)上为增函数;
同理,若0<a<1,则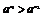 ,
,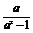 <0,
<0,
f(x1)-f(x2)=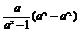 (1+
(1+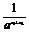 )<0,
)<0,
即f(x1)<f(x2),f(x)在(-∞,+∞)上为增函数.
综上,f(x)在R上为增函数.
(2)f(x)=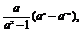 则f(-x)=
则f(-x)=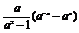 ,
,
显然f(-x)=-f(x). f(1-m)+f(1-m2)<0,
即f(1-m)<-f(1-m2) f(1-m)<f(m2-1),
f(1-m)<f(m2-1),
函数为增函数,且x∈(-1,1),故解-1<1-m<m2-1<1,可得1<m<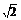 .
.
10.已知函数f(x)=(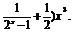
(1)求f(x)的定义域;
(2)讨论f(x)的奇偶性;
(3)证明:f(x)>0.
(1)解 由2x-1≠0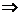 x≠0,∴定义域为(-∞,0)∪(0,+∞).
x≠0,∴定义域为(-∞,0)∪(0,+∞).
(2)解 f(x)=(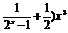
可化为f(x)=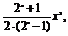
则f(-x)=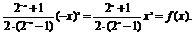
∴f(x)=(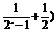 x3是偶函数.
x3是偶函数.
(3)证明 当x>0时,2x>1,x3>0.
∴(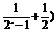 x3>0.
x3>0.
∵f(x)为偶函数,∴当x<0时,f(x)=f(-x)>0.
综上可得f(x)>0.
9.要使函数y=1+2x+4xa在x∈(-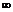 ,1]上y>0恒成立,求a的取值范围.
,1]上y>0恒成立,求a的取值范围.
解 由题意得1+2x+4xa>0在x∈(-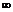 ,1]上恒成立,即a>-
,1]上恒成立,即a>-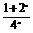 在x∈(-∞,1]上恒成立.
在x∈(-∞,1]上恒成立.
又∵-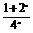 =-(
=-(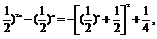
∵x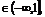 ∴(
∴(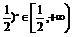 .令t=(
.令t=(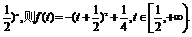
则f(t)在[ ,+
,+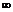 )上为减函数,
)上为减函数,
f(t)≤f(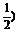 =-(
=-(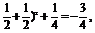
即f(t)∈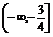 .
.
∵a>f(t),∴a∈(-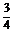 ,+
,+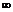 ).
).
8.函数y=ax(a>0,且a≠1)在[1,2]上的最大值比最小值大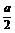 ,则a的值是 .
,则a的值是 .
答案  或
或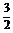
7.若函数f(x)=ax-1 (a>0,a≠1)的定义域和值域都是[0,2],则实数a等于 .
答案 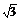
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com