
5.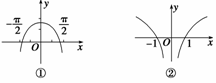 已知函数y=f(x)的图象如图①所示,
已知函数y=f(x)的图象如图①所示,
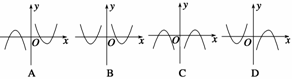 y=g(x)的图象如图②所示,则函数y=f(x)·g(x)的图象可能是图中的
(
)
y=g(x)的图象如图②所示,则函数y=f(x)·g(x)的图象可能是图中的
(
)
答案?C?
4.(2009·郑州模拟)定义运算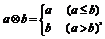 则函数f(x)=
则函数f(x)=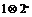 的图象是
( )
的图象是
( )
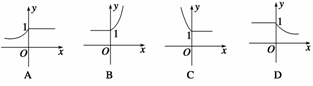
答案?A?
3.函数y=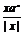 (0<a<1)的图象的大致形状是
(
)
(0<a<1)的图象的大致形状是
(
)
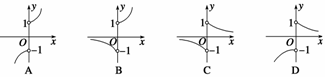
答案?D?
2.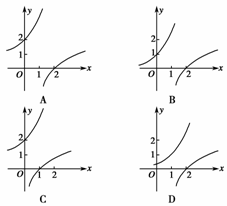 若函数f(x)的反函数为f -1(x),则函数f(x-1)与f -1(x-1)的图象可能是
(
)
若函数f(x)的反函数为f -1(x),则函数f(x-1)与f -1(x-1)的图象可能是
(
)
答案 D
1.(2008·辽宁理,8)将函数y=2x+1的图象按向量a平移得到函数y=2x+1的图象,则 ( )
?A.a=(-1,-1) B.a=(1,-1) C.a=(1,1) D.a=(-1,1)
答案?A?
3.当x∈(1,2)时,不等式(x-1)2<logax恒成立,则a的取值范围为 .
答案 (1,2]

2.设a>1,实数x,y满足|x|-loga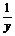 =0,则y关于x的函数的图象形状大致是 ( )
=0,则y关于x的函数的图象形状大致是 ( )
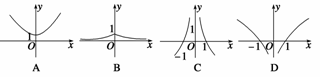
答案?B?
1.作出下列各个函数的图象:
(1)y=2-2x;
(2)y=|log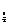 (1-x)|;
(1-x)|;
(3)y=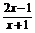 .
.
解 (1)由函数y=2x的图象关于x轴对称可得到y=-2x的图象,再将图象向上平移2个单位,可得y=2-2x的图象.如图甲.
(2)由y=log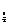 x的图象关于y轴对称,可得y=log
x的图象关于y轴对称,可得y=log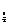 (-x)的图象,再将图象向右平移1个单位,即得到y=log
(-x)的图象,再将图象向右平移1个单位,即得到y=log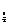 (1-x).然后把x轴下方的部分翻折到x轴上方,可得到y=|log
(1-x).然后把x轴下方的部分翻折到x轴上方,可得到y=|log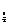 (1-x)|的图象.如图乙.
(1-x)|的图象.如图乙.
(3)y=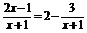 .
.
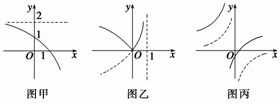 先作出y=-
先作出y=-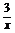 的图象,如图丙中的虚线部分,然后将图象向左平移1个单位,向上平移2个单位,即得到所求图象.如图丙所示的实线部分.
的图象,如图丙中的虚线部分,然后将图象向左平移1个单位,向上平移2个单位,即得到所求图象.如图丙所示的实线部分.
5.把下面不完整的命题补充完整,并使之成为真命题.
若函数f(x)=3+log2x的图象与g(x)的图象关于 对称,则函数g(x)= (注:填上你认为可以成为真命题的一种情形即可,不必考虑所有可能的情形).
答案 y=x 2x-3?(答案不惟一)

例1 作出下列函数的图象.
(1)y= (lgx+|lgx|);
(lgx+|lgx|);
(2)y=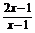 ;
;
(3)y=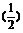 |x|.
|x|.
解 (1)y=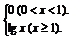
(2)由y=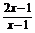 ,得y=
,得y=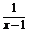 +2.
+2.
作出y=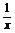 的图象,将y=
的图象,将y=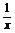 的图象向右平移一个单位,再向上平移2个单位得y=
的图象向右平移一个单位,再向上平移2个单位得y=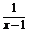 +2的图象.
+2的图象.
(3)作出y=(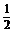 )x的图象,保留y=(
)x的图象,保留y=( )x图象中x≥0的部分,加上y=(
)x图象中x≥0的部分,加上y=( )x的图象中x>0的部分关于y轴的对称部分,即得y=(
)x的图象中x>0的部分关于y轴的对称部分,即得y=(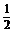 )|x|?的图象.其图象依次如下:
)|x|?的图象.其图象依次如下:
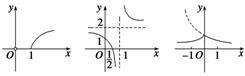
例2 函数y=f(x)与函数y=g(x)的图象如图,则函数y=f(x)·g(x)的图象可能是 ( )
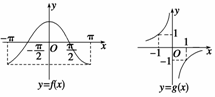
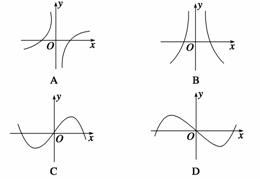
答案?A?
例3 (13分)设a>1,函数f(x)=ax+1-2.
(1)求f(x)的反函数f -1(x);
(2)若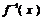 在[0,1]上的最大值与最小值互为相反数,求a的值;
在[0,1]上的最大值与最小值互为相反数,求a的值;
(3)若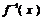 的图象不经过第二象限,求a的取值范围.
的图象不经过第二象限,求a的取值范围.
解 (1)因为ax+1>0,
所以f(x)的值域是{y|y>-2}. 2分
设y=ax+1-2,解得x=loga(y+2)-1.
所以f(x)的反函数为
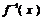 =loga(x+2)-1,(x>-2).
4分
=loga(x+2)-1,(x>-2).
4分
(2)当a>1时,函数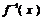 =loga(x+2)-1为(-2,+∞)上的增函数,所以
=loga(x+2)-1为(-2,+∞)上的增函数,所以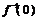 +
+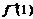 =0,
=0,
即(loga2-1)+(loga3-1)=0,解得a=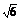 .
8分
.
8分
(3)当a>1时,函数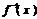 是(-2,+∞)上的增函数,且经过定点(-1,-1).
是(-2,+∞)上的增函数,且经过定点(-1,-1).
所以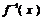 的图象不经过第二象限的充要条件是
的图象不经过第二象限的充要条件是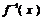 的图象与x轴的交点位于x轴的非负半轴上.11分
的图象与x轴的交点位于x轴的非负半轴上.11分
令loga(x+2)-1=0,解得x=a-2,
由a-2≥0,解得a≥2. 13分

4.(2008·四川理,4)将直线y=3x绕原点逆时针旋转90°,再向右平移1个单位长度,所得到的直线为( )
?A.y=-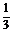 x+
x+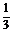 B.y=-
B.y=-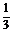 x+1
C.y=3x-3?
D.y=
x+1
C.y=3x-3?
D.y=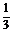 x+1
x+1
答案?A?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com