
23.(本小题满分10分)
已知函数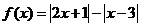 .
.
(Ⅰ)解不等式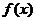 ≤4;
≤4;
(Ⅱ)若存在x使得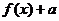 ≤0成立,求实数a的取值范围.
≤0成立,求实数a的取值范围.
22.(本小题满分10分)
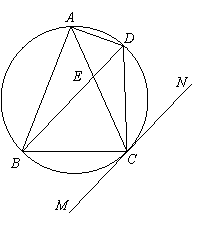
如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.
(Ⅰ)求证:△ABE≌△ACD;
(Ⅱ)若AB=6,BC=4,求AE.
21.(本小题满分12分)
已知函数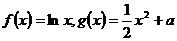 (
(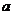 为常数),直线l与函数
为常数),直线l与函数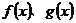 的图象都相切,且l与函数
的图象都相切,且l与函数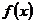 的图象的切点的横坐标为l.
的图象的切点的横坐标为l.
(Ⅰ)求直线l的方程及a的值;
(Ⅱ)当k>0时,试讨论方程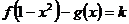 的解的个数.
的解的个数.
请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.
20.(本小题满分12分)
设椭圆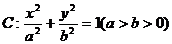 的离心率,
的离心率,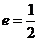 右焦点到直线
右焦点到直线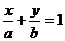 的距离
的距离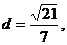
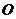 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆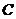 的方程;
的方程;
(II)过点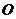 作两条互相垂直的射线,与椭圆
作两条互相垂直的射线,与椭圆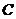 分别交于
分别交于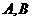 两点,证明:点
两点,证明:点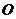 到直线
到直线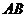 的距离为定值,并求弦
的距离为定值,并求弦 长度的最小值.
长度的最小值.
19.(本小题满分12分)
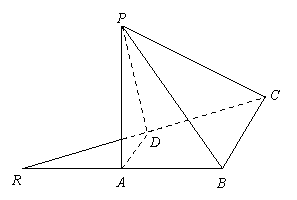 已知等腰直角三角形
已知等腰直角三角形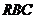 ,其中∠
,其中∠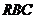 =90º,
=90º,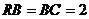 .点
.点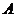 、
、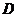 分别是
分别是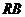 、
、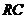 的中点,现将△
的中点,现将△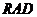 沿着边
沿着边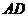 折起到△
折起到△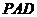 位置,使
位置,使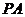 ⊥
⊥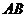 ,连结
,连结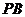 、
、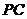 .
.
(Ⅰ)求证: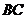 ⊥
⊥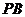 ;
;
(Ⅱ)求二面角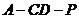 的余弦值.
的余弦值.
18.(本小题满分12分)
某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛得分的情况用如图所示的茎叶图表示.
(Ⅰ)求甲、乙两名运动员得分的中位数;
(Ⅱ)你认为哪位运动员的成绩更稳定?
(Ⅲ)如果从甲、乙两位运动员的7场得分中各随机抽取一场的得分,求甲的得分大于乙的得分的概率.
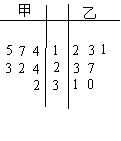
17.(本小题满分12分)
已知函数 的最小正周期为
的最小正周期为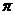 .
.
 (Ⅰ)求
(Ⅰ)求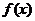 ;
;
(Ⅱ)当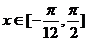 时,求函数
时,求函数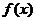 的值域.
的值域.
16.设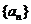 是一个公差为
是一个公差为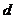 (
(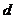 >0)的等差数列.若
>0)的等差数列.若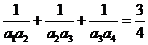 ,且其前6项的和
,且其前6项的和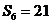 ,则
,则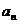 = .
= .
15.若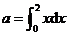 ,则在
,则在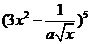 的二项展开式中,常数项为
.
的二项展开式中,常数项为
.
14.在全运会期间,5名志愿者被安排参加三个不同比赛项目的接待服务工作,则每个项
目至少有一人参加的安排方法有 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com