
4.有5条线段,其长度分别为1、3、5、7、9,现从中任取3条线段,求3条线段构成三角形的概率.
3.停车场可把12辆车停放一排,当有8辆车已停放后,则所剩4个空位恰连在一起的概率为 ( )
A、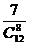 B、
B、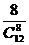 C、
C、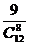 D、
D、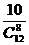
2.先后抛掷三枚均匀的硬币,至少出现一次正面的概率是 ( )
A、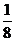 B、
B、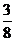 C、
C、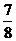 D、
D、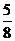
1.对某电视机厂生产的电视机进行抽样检测的数据如下:
|
抽取台数 |
50 |
100 |
200 |
300 |
500 |
1000 |
|
优等品数 |
40 |
92 |
192 |
285 |
478 |
954 |
(1)计算表中优等品的各个频率;
(2)该厂生产的电视机优等品的概率是多少?
[例1] 某人有5把钥匙,但忘记了开房门的是哪一把,于是,他逐把不重复地试开,问恰好第三次打开房门锁的概率是多少?
错解:有5把钥匙,每次打开房门的概率都是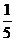 ,不能打开房门的概率是
,不能打开房门的概率是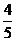 ,因而恰好第三次打开房门的概率是
,因而恰好第三次打开房门的概率是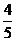 ×
×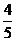 ×
×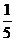 =
=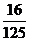 .
.
错因:上述解法忽略了条件“逐把不重复地试开”.
正解:我们知道最多开5次门,且其中有且仅有一次可以打开房门,故每一次打开门的概率是相同的,都是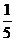 .开三次门的所有可能性有
.开三次门的所有可能性有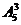 种.第三次打开房门,则房门钥匙放在第3号位置上,前两次没能打开门,则前2个位置是用另4把钥匙安排的,故有
种.第三次打开房门,则房门钥匙放在第3号位置上,前两次没能打开门,则前2个位置是用另4把钥匙安排的,故有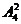 种可能.从而恰好第三次打开房门锁的概率是P(A)=
种可能.从而恰好第三次打开房门锁的概率是P(A)=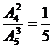 .
.
[例2] 某组有16名学生,其中男、女生各占一半,把全组学生分成人数相等的两小组,求每小组里男、女生人数相同的概率.
错解:把全组学生分成人数相等的两小组,有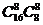 种分法,事件A为组里男、女生各半的情形,它有
种分法,事件A为组里男、女生各半的情形,它有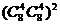 种,所以P(A)=
种,所以P(A)=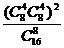 .
.
错因:这里没注意到均匀分成两组与分成A、B两组的区别.
正解:基本事件有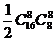 ,事件A为组里男、女生各半的情形,它有
,事件A为组里男、女生各半的情形,它有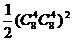 种,所以 P(A)=
种,所以 P(A)=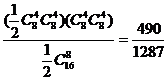 .
.
[例3] 把一枚硬币向上连抛10次,则正、反两面交替出现的概率是 .
错解:抛掷一枚硬币出现正、反两面的可能性都相等,因而正、反两面交替出现的概率是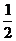 .
.
错因:没审清题意.事实上,把一枚硬币向上连抛10次,出现正面5次的概率同样也不等于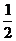 .
.
正解:连抛10次得正、反面的所有可能的情况共有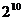 种,而题设中的正、反两面交替出现的情况只有2种,故所求的概率为
种,而题设中的正、反两面交替出现的情况只有2种,故所求的概率为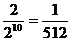 .
.
[例4]某科研合作项目成员由11个美国人、4个法国人和5个中国人组成,现从中随机选出两位作为成果发布人,则此两人不属于同一个国家的概率为 (结果用分数表示).
解:设“从20名成员中随机选出的2人来自不同国家”为事件A,则A所包含的基本事件数为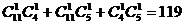 ,又基本事件数为
,又基本事件数为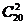 .
.
故P(A)=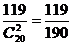 .
.
[例5] 将4个编号的球放入3个编号的盒中,对于每一个盒来说,所放的球数k满足0≤k≤4.在各种放法的可能性相等的条件下,求:
(1)第一个盒没有球的概率;
(2)第一个盒恰有1个球的概率;
(3)第一个盒恰有2个球的概率;
(4)第一个盒有1个球,第二个盒恰有2个球的概率.
解:4个不同的球放入3个不同的盒中的放法共有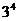 种.
种.
(1)第一个盒中没有球的放法有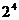 种,所以第一个盒中没有球的概率为:
种,所以第一个盒中没有球的概率为:
P1=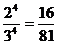 .
.
(2)第一个盒中恰有1个球的放法有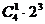 种,所以第一个盒中恰有1个球的概率为: P2=
种,所以第一个盒中恰有1个球的概率为: P2=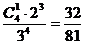 .
.
(3)第一个盒中恰有2个球的放法有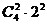 种,所以第一个盒中恰有2个球的概率为: P3=
种,所以第一个盒中恰有2个球的概率为: P3=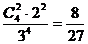 .
.
(4)第一个盒中恰有1个球,第二个盒中恰有2个球的放法有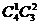 种,所以所求的概率为:P4=
种,所以所求的概率为:P4=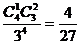 .
.
[例6] 一个口袋内有7个白球和3个黑球,分别求下列事件的的概率:
(1)事件A:从中摸出一个放回后再摸一个,两回摸出的球是一白一黑;
(2)事件B:从袋中摸出一个黑球,放回后再摸出一个是白球;
(3)事件C:从袋中摸出两个球,一个黑球,一个白球;
(4)事件D:从从袋中摸出两个球,先摸出的是黑球,后摸出的是白球.
解:(1)基本事件总数是10×10.事件A包括“先摸出黑球后摸出白球”及“先摸出白球后摸出黑球”,摸出白球及黑球分别有7种和3种可能.所以A发生共有2×7×3种可能. ∴P(A)=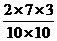 =0.42.
=0.42.
2)事件B与事件A不同,它确定了先摸黑球再摸白球的顺序.
P(B)=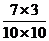 =0.21
=0.21
(3)事件C说明摸出两个球不放回,且不考虑次序,因此基本事件总数是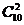 ,事件C包含的基本事件个数是
,事件C包含的基本事件个数是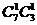 .
.
P(C)=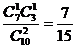 ≈0.47.
≈0.47.
(4)与事件A相比,D要考虑摸出两球的先后次序.
P(D)=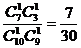 ≈0.23
≈0.23
评注:注意“放回抽样”与“不放回抽样”的区别.本例(1)(2)是放回抽样,(3)(4)是不放回抽样.
5.注意用集合的观点来看概率,运用图式法来弄清各事件之间的关系.对古典概率来说,一次试验中等可能出现的几个结果组成一个集合I,其中各基本事件均为集合I的含有一个元素的子集,包括m个基本事件的子集A,从而从集合的角度来看:事件A的概率是子集A的元素的个数与集合I的元素个数的比值,即P(A)=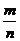 .因此,可以借助集合的表示法来研究事件,运用图示法弄清各事件的关系,从而做到较深刻的理解.
.因此,可以借助集合的表示法来研究事件,运用图示法弄清各事件的关系,从而做到较深刻的理解.
4.等可能事件的理解:一次试验中所有可能的n个基本结果出现的可能性都相等,这n个结果对应着n个基本事件.对等可能事件的理解,其实质在于对等可能性的理解.“等可能性”指的是结果,而不是事件.例如抛掷两枚均匀的硬币,可能出现“两个正面”“两个反面”“一正一反”“一反一正”这四种结果,每一种结果的可能性相等,都是0.25;而出现“两个正面”“两个反面”“一正一反”这三种结果就不是等可能的.
3.必然事件的概率为1,不可能事件的概率为0,随机事件的概率:0<P(A)<1,这里要辩证地理解它们的概率:必然事件和不可能事件可以看作随机事件的两个极端,它们虽是两类不同的事件,但在一定的情况下又可以统一起来,即任意事件A的概率满足:
0≤P(A)≤1
2.频率与概率:随机事件A的频率指此事件发生的次数m与试验总次数n的比值,它是随着试验次数的改变而变化的,它具有一定的稳定性,即总在某个常数p附近摆动,且随着试验次数的不断增多,这种摆动幅度越来越小,于是,我们给这个常数取个名字,叫随机事件的概率.因此,概率从数量上反映了随机事件发生的可能性的大小;而频率在大量重复试验的前提下,可近似地作为这个事件的概率.即概率是频率的稳定值,频率是概率的近似值.
1.必然事件、不可能事件、随机事件的区别与联系:必然事件是指在一定条件下必然发生的事件;不可能事件是指在一定的条件下不可能发生的事件;随机事件是指在一定的条件下可能发生也可能不发生的事件.要辨析清事件的条件和结果,理解事件的结果是相应于“一定条件”而言的,必须明确什么是事件发生的条件,什么是在此条件下产生的结果.上述三种事件都是在一定条件下的结果.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com