
9.求函数f(x)=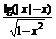 的定义域.
的定义域.
解 由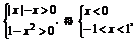
∴-1<x<0.
∴函数f(x)= 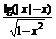 的定义域为(-1,0).
的定义域为(-1,0).
8.已知函数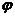 (x)=f(x)+g(x),其中f(x)是x的正比例函数,g(x)是x的反比例函数,且
(x)=f(x)+g(x),其中f(x)是x的正比例函数,g(x)是x的反比例函数,且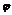 (
(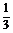 )=16,
)=16, 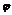 (1)=8,则
(1)=8,则
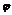 (x)= .
(x)= .
答案 3x+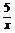
7.已知函数f(x),g(x)分别由下表给出
|
x |
1 |
2 |
3 |
|
f(x) |
1 |
3 |
1 |
|
x |
1 |
2 |
3 |
|
g(x) |
3 |
2 |
1 |
则f[g(1)]的值为 ,满足f[g(x)]>g[f(x)]的x的值是 .
答案 1 2
6.(2008·陕西理,11)定义在R上的函数f(x)满足f(x+y)=f(x)+f(y)+2xy(x,y∈R),f(1)=2,则f(-3)= .
答案 6
5.函数f(x)=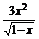 +lg(3x+1)的定义域是
.
+lg(3x+1)的定义域是
.
答案 (-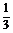 ,1)
,1)
4.已知f(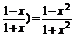 ,则f(x)的解析式为
.
,则f(x)的解析式为
.
答案 f(x)=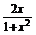
3.若f(x)=
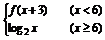 ,则f(-1)的值为 .
,则f(-1)的值为 .
答案 3
2.(2008·安徽文,13)函数f(x)=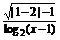 的定义域为
.
的定义域为
.
答案 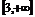
1.设函数f1(x)=x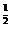 ,f2(x)=x-1,f3(x)=x2,则
,f2(x)=x-1,f3(x)=x2,则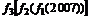 =
.
=
.
答案 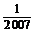
12.偶函数f(x)=ax4+bx3+cx2+dx+e的图象过点P(0,1),且在x=1处的切线方程为y=x-2,求y=f(x)的解析式.
解 ∵f(x)的图象过点P(0,1),∴e=1. ①
又∵f(x)为偶函数,∴f(-x)=f(x).
故ax4+bx3+cx2+dx+e=ax4-bx3+cx2-dx+e.
∴b=0,d=0. ②
∴f(x)=ax4+cx2+1.
∵函数f(x)在x=1处的切线方程为y=x-2,
∴可得切点为(1,-1).
∴a+c+1=-1. ③
∵f′(1)=(4ax3+2cx)|x=1=4a+2c,
∴4a+2c=1. ④
由③④得a=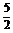 ,c=-
,c=-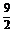 .
.
∴函数y=f(x)的解析式为f(x)=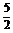 x4-
x4-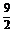 x2+1.
x2+1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com