
1.求使直线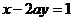 和
和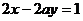 平行的实数
平行的实数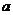 的取值。(答案:
的取值。(答案: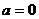 )
)
例1 两条直线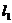 :
: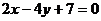 ,
, 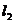 :
: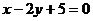 .
.
求证: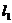 ∥
∥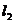
证法一:因为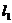 :
: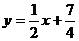 ,
,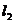 :
: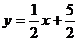
所以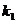 =
=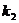 且
且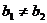 ,∴
,∴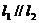 .
.
证法二:∵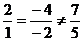 ,∴
,∴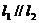
例2 求过点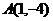 且与直线
且与直线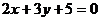 平行的直线方程.
平行的直线方程.
解一:已知直线的斜率为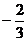 ,因为所求直线与已知直线平行,因此它的斜率也是
,因为所求直线与已知直线平行,因此它的斜率也是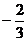

根据点斜式,得到所求直线的方程是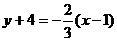
即
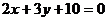 .
.
解二:设与直线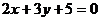 平行的直线
平行的直线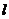 的方程为
的方程为
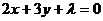
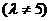 ,
,
∵ 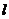 经过点
经过点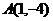 ,∴
,∴ 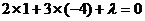 ,解之得
,解之得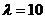
∴ 所求直线方程为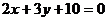 .
.
注意:①解法一求直线方程的方法是通法,必须掌握;
②解法二是常常采用的解题技巧。一般地,直线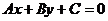 中系数
中系数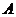 、
、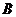 确定直线的斜率,因此,与直线
确定直线的斜率,因此,与直线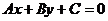 平行的直线方程可设为
平行的直线方程可设为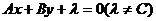 ,其中
,其中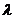 待定
待定 (直线系)
(直线系)
例3求与直线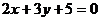 平行,且在两坐标轴上的截距之和为
平行,且在两坐标轴上的截距之和为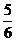 的直线的方程.
的直线的方程.
解:设直线的方程为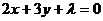
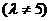 ,令
,令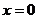 ,则在
,则在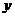 轴上的截距为
轴上的截距为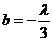 ;令
;令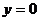 ,则在
,则在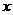 轴上的截距为
轴上的截距为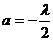 ,
,
由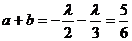 得
得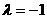 ,∴所求直线方程为
,∴所求直线方程为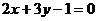 .
.
例4 已知直线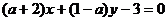 与
与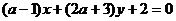 互相垂直,求
互相垂直,求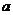 的值.
的值.
解 :
∵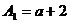 ,
,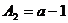 ,
,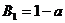 ,
,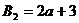 且两直线互相垂直
且两直线互相垂直
∴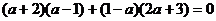 ,解之得
,解之得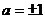

注意:若用斜率来解,则需讨论
例5 求过点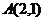 ,且与直线
,且与直线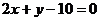 垂直的直线
垂直的直线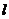 的方程.
的方程.
分析:一般地,由于与直线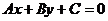 垂直的直线的斜率互为负倒数,故可得其方程为
垂直的直线的斜率互为负倒数,故可得其方程为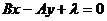 ,这是常常用到的解题技巧(直线系方程)
,这是常常用到的解题技巧(直线系方程)
解:设与直线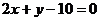 垂足的直线方程为
垂足的直线方程为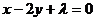
∵直线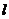 经过点
经过点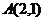 ,∴
,∴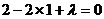 ,解得
,解得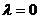

故所求的方程为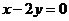

2.斜率存在时两直线的平行与垂直.
设直线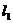 和
和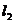 的斜率为
的斜率为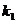 和
和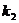 ,它们的方程分别是:
,它们的方程分别是:
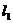 :
: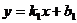 ;
; 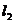 :
: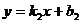 .
.
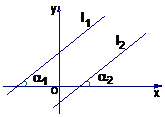 两直线的平行与垂直是由两直线的方向来决定的,两直线的方向又是由直线的倾斜角与斜率决定的,所以我们下面要解决的问题是两平行与垂直的直线它们的斜率有什么特征
两直线的平行与垂直是由两直线的方向来决定的,两直线的方向又是由直线的倾斜角与斜率决定的,所以我们下面要解决的问题是两平行与垂直的直线它们的斜率有什么特征
⑴两条直线平行(不重合)的情形.
如果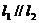 ,那么它们的倾斜角相等:
,那么它们的倾斜角相等: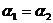 ,∴
,∴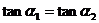 .即
.即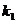 =
=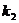 .
.
反过来,如果两条直线的斜率相等,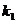 =
=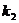 ,那么
,那么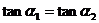 .由于0°≤
.由于0°≤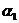 <180°, 0°≤
<180°, 0°≤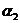 <180°,∴
<180°,∴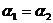 .∵两直线不重合,∴
.∵两直线不重合,∴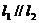 .
.
两条直线有斜率且不重合,如果它们平行,那么它们的斜率相等;反之,如果它们的斜率相等,则它们平行,即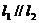
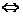
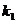 =
=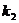 且
且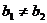

要注意,上面的等价是在两直线不重合且斜率存在的前提下才成立的,缺少这个前提,结论并不存立.
思考1:已知直线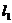 、
、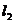 的方程为
的方程为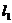 :
: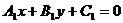 ,
,
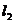 :
: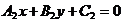
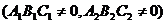
求证: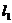 ∥
∥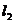 的充要条件是
的充要条件是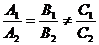

 ⑵两条直线垂直的情形:如果两条直线的斜率分别是
⑵两条直线垂直的情形:如果两条直线的斜率分别是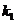 和
和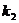 ,则这两条直线垂直的充要条件是
,则这两条直线垂直的充要条件是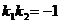 .
.
用倾斜角的关系推导:如果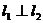 ,这时
,这时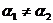 ,否则两直线平行
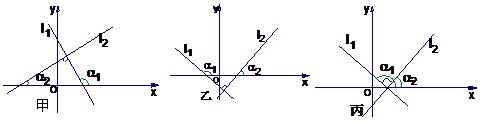
,否则两直线平行 设
设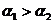 ,甲图的特征是
,甲图的特征是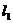 与
与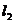 的交点在x轴上方;乙图的特征是
的交点在x轴上方;乙图的特征是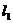 与
与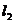 的交点在x轴下方;丙图的特征是
的交点在x轴下方;丙图的特征是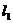 与
与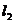 的交点在x轴上,无论哪种情况下都有
的交点在x轴上,无论哪种情况下都有
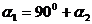 .因为
.因为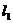 和
和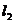 的斜率为
的斜率为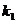 和
和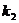 ,即
,即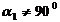 ,所以
,所以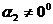

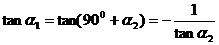 ,即
,即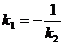 或
或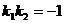

反过来,如果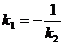 或
或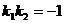
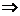
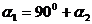
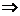
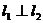 .
.
两条直线都有斜率,如果它们互相垂直,则它们的斜率互为负倒数;反之,如果它们的斜率互为负倒数,则它们互相垂直,即
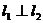
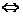
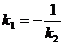
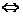
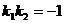

用向量关系推导:设直线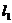 和
和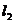 的斜率分别是
的斜率分别是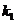 和
和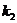 ,则直线
,则直线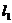 有方向向量
有方向向量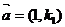 ,直线
,直线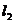 有方向向量
有方向向量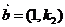 ,根据平面向量的有关知识,有
,根据平面向量的有关知识,有
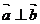
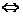
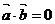
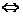
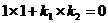 即
即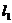
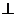
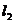
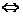
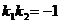
所以,如果两条直线的斜率分别是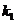 和
和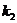 ,则这两条直线垂直的充要条件是
,则这两条直线垂直的充要条件是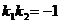 .
.
思考2:已知直线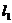 和
和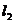 的一般式方程为
的一般式方程为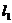 :
: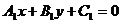 ,
,
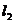 :
: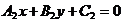 ,则
,则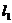
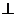
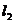
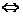
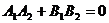

1.特殊情况下的两直线平行与垂直.
当两条直线中有一条直线没有斜率时:
(1)当另一条直线的斜率也不存在时,两直线的倾斜角都为90°,互相平行;
(2)当另一条直线的斜率为0时,一条直线的倾斜角为90°,另一条直线的倾斜角为0°,两直线互相垂直
|
直线名称 |
已知条件 |
直线方程 |
使用范围 |
示意图 |
|
点斜式 |
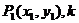 |
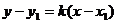 |
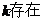 |
|
|
斜截式 |
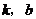 |
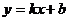 |
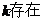 |
|
|
两点式 |
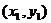 ( (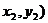 |
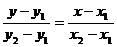 |
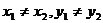 |
|
|
截距式 |
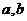 |
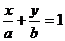 |
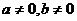 |
|
|
一般式 |
A、B、C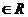 |
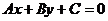 |
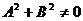 |
|
判断正误,并举例说明:(画“√”或“×”)
⑴非金属氧化物一定是酸性氧化物( )如
⑵酸性氧化物一定是非金属氧化物( )如
⑶金属氧化物一定是碱性氧化物 ( )如
⑷碱性氧化物一定是金属氧化物 ( )如
⑸酸酐一定是酸性氧化物 ( × )如 乙酸酐
2.不成盐氧化物:如CO、NO
1.成盐氧化物:
⑴酸性氧化物:如SO3 + NaOH =
⑵碱性氧化物:如 MgO + H2SO4 =
⑶两性氧化物:如 Al2O3 + HCl =
Al2O3 + NaOH =
⑷复杂氧化物:如Na2O2、KO2、Fe3O4、Pb3O4
Na2O2 + HCl =
Fe3O4 + HCl(浓) =
Pb3O4 + HCl(浓) =
3、用向量加法证明:两条对角线互相平分的四边形是平行四边形
3°注意:| +
+ | ≤ |
| ≤ | | + |
| + | |,当且仅当方向相同时取等号
|,当且仅当方向相同时取等号
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com