
4、一艘船以5km/h的速度在行驶,同时河水的流速为2km/h,则船的实际航行速度大小最大是 km/h,最小是
km/h,最小是 km/h
km/h
3、一艘船从A点出发以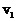 的速度向垂直于对岸的方向行驶,同时河水的流速为
的速度向垂直于对岸的方向行驶,同时河水的流速为 ,船的实际航行的速度的大小为
,船的实际航行的速度的大小为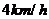 ,方向与水流间的夹角是
,方向与水流间的夹角是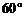 ,求
,求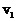 和
和

2、一艘船距对岸 ,以
,以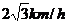 的速度向垂直于对岸的方向行驶,到达对岸时,船的实际航程为8km,求河水的流速
的速度向垂直于对岸的方向行驶,到达对岸时,船的实际航程为8km,求河水的流速
1、一艘船从A点出发以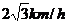 的速度向垂直于对岸的方向行驶,船的实际航行的速度的大小为
的速度向垂直于对岸的方向行驶,船的实际航行的速度的大小为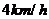 ,求水流的速度
,求水流的速度
例1如图,一艘船从A点出发以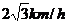 的速度向垂直于对岸的方向行驶,同时河水的流速为
的速度向垂直于对岸的方向行驶,同时河水的流速为 ,求船的实际航行的速度的大小与方向(用与流速间的夹角表示).
,求船的实际航行的速度的大小与方向(用与流速间的夹角表示).
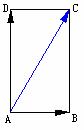 解:设
解:设 表示船垂直于对岸行驶的速度,
表示船垂直于对岸行驶的速度,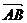 表示水流的速度,以AD,AB为邻边作平行四边形ABCD,则
表示水流的速度,以AD,AB为邻边作平行四边形ABCD,则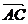 就是船的实际航行的速度.
就是船的实际航行的速度.
在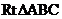 中,
中,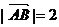 ,
,
所以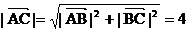
因为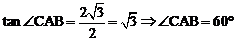
答:船的实际航行的速度的大小为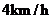 ,方向与水流速间的夹角为
,方向与水流速间的夹角为
3.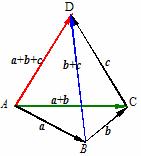 向量加法的结合律:(
向量加法的结合律:( +
+ ) +
) +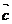 =
= + (
+ ( +
+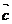 )
)
证:如图:使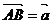 ,
,  ,
, 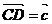
则( +
+ ) +
) +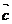 =
=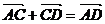
 + (
+ ( +
+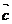 ) =
) =
∴( +
+ ) +
) +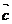 =
= + (
+ ( +
+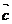 )
)
从而,多个向量的加法运算可以按照任意的次序、任意的组合来进行
2.向量加法的交换律: +
+ =
= +
+
1. 向量的加法:求两个向量和的运算,叫做向量的加法
几何中向量加法是用几何作图来定义的,一般有两种方法,即向量加法的三角形法则(“首尾相接,首尾连”)和平行四边形法则(对于两个向量共线不适应) 课本中采用了三角形法则来定义,这种定义,对两向量共线时同样适用,当向量不共线时,向量加法的三角形法则和平行四边形法则是一致的
课本中采用了三角形法则来定义,这种定义,对两向量共线时同样适用,当向量不共线时,向量加法的三角形法则和平行四边形法则是一致的
如图,已知向量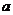 、
、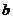
 在平面内任取一点
在平面内任取一点 ,作
,作 ,
,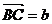 ,则向量
,则向量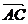 叫做
叫做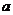 与
与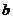 的和,记作
的和,记作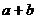 ,即
,即 
特殊情况:

对于零向量与任一向量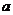 ,有
,有 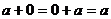
探究:(1)两相向量的和仍是一个向量;
(2)当向量 与
与 不共线时,
不共线时, +
+ 的方向不同向,且|
的方向不同向,且| +
+ |<|
|<| |+|
|+| |;
|;
(3)当 与
与 同向时,则
同向时,则 +
+ 、
、 、
、 同向,且|
同向,且| +
+ |=|
|=| |+|
|+| |,当
|,当 与
与 反向时,若|
反向时,若| |>|
|>| |,则
|,则 +
+ 的方向与
的方向与 相同,且|
相同,且| +
+ |=|
|=| |-|
|-| |;若|
|;若| |<|
|<| |,则
|,则 +
+ 的方向与
的方向与 相同,且|
相同,且| +b|=|
+b|=| |-|
|-| |.
|.
(4)“向量平移”(自由向量):使前一个向量的终点为后一个向量的起点,可以推广到n个向量连加
7.对向量概念的理解
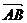 的字母是有顺序的,起点在前终点在后,所以我们说有向线段有三个要素:起点、方向、长度;既有大小又有方向的量,我们叫做向量,有二个要素:大小、方向.向量不能比较大小;实数与向量不能相加减,但实数与向量可以相乘.
的字母是有顺序的,起点在前终点在后,所以我们说有向线段有三个要素:起点、方向、长度;既有大小又有方向的量,我们叫做向量,有二个要素:大小、方向.向量不能比较大小;实数与向量不能相加减,但实数与向量可以相乘.
向量与有向线段的区别:向量是自由向量,只有大小和方向两个要素;与起点无关:只要大小和方向相同,则这两个向量就是相同的向量;有向线段有起点、大小和方向三个要素,起点不同,尽管大小和方向相同,也是不同的有向线段
6.共线向量与平行向量关系:
平行向量就是共线向量,这是因为任一组平行向量都可移到同一直线上.
(1)平行向量可以在同一直线上,要区别于两平行线的位置关系;
(2)共线向量可以相互平行,要区别于在同一直线上的线段的位置关系.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com