
3.命题“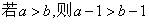 ”的否命题是( )
”的否命题是( )
A.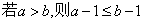 B.
B.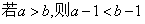
C.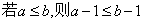 D.
D. 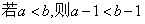
2.已知集合M={12,a},集合N={x|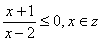 },且
},且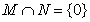 ,
,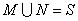 ,
,
则集合S的真子集的个数为( )
A. 8 B. 7 C. 16 D.15
1. 集合A={(x,y)|x+y=0}, B={(x,y)|x-y=2},则A∩B是 ( )
(A) (1,-1) (B) 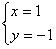 (C) {(1,-1)} (D) {(x,y)|x=1或y=-1}
(C) {(1,-1)} (D) {(x,y)|x=1或y=-1}
6.九个国家乒乓球队中有3个亚洲国家队,抽签分成甲、乙、丙三组(每组3队)进行预赛,试求:(1)三个组各有一个亚洲国家队的概率;(2)至少有两个亚洲国家队分在同一组的概率.
5.某班级有52个人,一年若按365天计算,问至少有两个人的生日在同一天的概率为多大?
4.设有编号分别为1,2,3,4,5的五封信,另有同样编号的五个信封,现将五封信任意装入五个信封,每个信封装入一封信,试求至少有两封信配对的概率.
3. 某小组有男生6人,女生4人,现从中选出2人去开会,求至少有1名女生的概率.
2. 取一个边长为2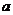 的正方形及其内切圆,随机向正方形内丢一粒豆子,求豆子落入圆内的概率.
的正方形及其内切圆,随机向正方形内丢一粒豆子,求豆子落入圆内的概率.
1. 从装有2个红球和2个黑球的口袋内任取2个球,那么互斥而不对立的两个事件是( )
A.至少有1个黑球,都是黑球 B.至少有1个黑球,至少有1个红球
 C.恰有1个黑球,恰有2个红球 D.至少有1个黑球,都是红球
C.恰有1个黑球,恰有2个红球 D.至少有1个黑球,都是红球
[例1] 从0,1,2,3这四位数字中任取3个进行排列,组成无重复数字的三位数,求排成的三位数是偶数的概率.
错解:记“排成的三位数是偶数”为事件A,
P(A)= =
=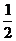 .
.
错因:上述解法忽略了排成的三位数首位不能为零.
正解:记“排成的三位数的个位数字是0”为事件A,“排成的三位数的个位数字是2”为事件B,且A与B互斥,则“排成的三位数是偶数”为事件A+B,于是
P(A+B)=P(A)+P(B)=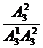 +
+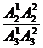 =
=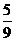 .
.
[例2] 从1,2,3,…,100这100个数中,随机取出两个数,求其积是3的倍数的概率.
错解:从1,2,3,…,100这100个数中,随机取出两个数,其积是3的倍数,则须所取两数至少有一个是3的倍数. 记事件A为任取两整数相乘为3的倍数,则
P(A)=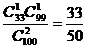
错因: 这里相关的排列组合问题没有过关.
正解:基本事件数有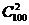 种.在由1到100这100个自然数中,3的倍数的数组成的集合M中有33个元素,不是3的倍数组成的集合N中有67个元素,事件A为任取两整数相乘为3的倍数,分两类:(1)取M中2个元素相乘有
种.在由1到100这100个自然数中,3的倍数的数组成的集合M中有33个元素,不是3的倍数组成的集合N中有67个元素,事件A为任取两整数相乘为3的倍数,分两类:(1)取M中2个元素相乘有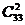 种;(2)从集合M、N中各取1个元素相乘有
种;(2)从集合M、N中各取1个元素相乘有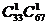 种.因为这两类互斥,所以
种.因为这两类互斥,所以
P(A)=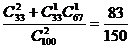 .
.
[例3] 在房间里有4个人,问至少有两个人的生日是同一个月的概率是多少?
解:由于事件A“至少有两个人的生日是同一个月”的对立事件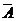 是“任何两个人的生日都不同月”.因而 至少有两个人的生日是同一个月的概率为:
是“任何两个人的生日都不同月”.因而 至少有两个人的生日是同一个月的概率为:
P(A)=1-P(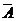 )=1-
)=1-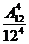 =1-
=1-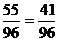 .
.
[例4] 某单位6名员工借助互联网开展工作,每个员工上网的概率都是0.5(相互独立).求(1)至少3人同时上网的概率;(2)至少几人同时上网的概率小于0.3?
解:(1)至少3人同时上网的概率等于1减去至多2人同时上网的概率,即
1-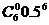 -
-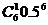 -
-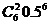 =1-
=1-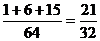 .
.
(2)6人同时上网的概率为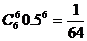 <0.3;
<0.3;
至少5人同时上网的概率为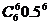 +
+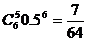 <0.3;
<0.3;
至少4人同时上网的概率为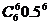 +
+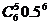 +
+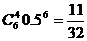 >0.3.
>0.3.
故至少5人同时上网的概率小于0.3.
[例5]设甲、乙两射手独立地射击同一目标,他们击中目标的概率分别为0.9、0.8,求:(1)目标恰好被甲击中的概率;(2)目标被击中的概率.
解:设事件A为“甲击中目标”,事件B为“乙击中目标”.
由于甲、乙两射手独立射击,事件A与B是相互独立的,
故A与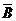 、
、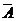 与B也是相互独立的.
与B也是相互独立的.
(1)目标恰好被甲击中,即事件A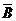 发生.
发生.
P(A·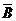 )=P(A)×P(
)=P(A)×P(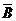 )=0.9×(1-0.8)=0.18.
)=0.9×(1-0.8)=0.18.
∴目标恰好被甲击中的概率为0.18.
(2)目标被击中即甲、乙两人中至少有1人击中目标,即事件A·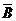 、
、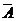 ·B、A·B发生.
·B、A·B发生.
由于事件A·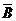 、
、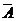 ·B、A·B彼此互斥,
·B、A·B彼此互斥,
所以目标被击中的概率为
P(A·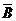 +
+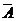 ·B+A·B)=P(A·
·B+A·B)=P(A·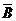 )+P(
)+P(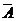 ·B)+P(A·B)
·B)+P(A·B)
=P(A)·P(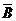 )+P(
)+P(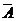 )·P(B)+P(A·B)
)·P(B)+P(A·B)
=0.9×0.2+0.1×0.8+0.9×0.8=0.98.
评注:运用概率公式求解时,首先要考虑公式的应用前提.本题(2)也可以这样考虑:排除甲、乙都没有击中目标.因为P(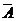 ·
·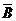 )=P(
)=P(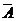 )·P(
)·P(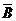 )=0.1×0.2=0.02.
)=0.1×0.2=0.02.
所以目标被击中的概率为
1-P(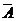 ·
·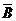 )=1-0.02=0.98.
)=1-0.02=0.98.
[例6]某课程考核分理论与实验两部分进行,每部分考核成绩只记“合格”与“不合格” ,两部分考核都是“合格”则该课程考核“合格”,甲、乙、丙三人在理论考核中合格的概率分别为0.9,0.8,0.7;在实验考核中合格的概率分别为0.8,0.7,0.9,所有考核是否合格相互之间没有影响.
(1)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
(2)求这三人课程考核都合格的概率.(结果保留三位小数)
解: 记“甲理论考核合格”为事件A1,“乙理论考核合格”为事件A2,“丙理论考核合格”为事件A3,“甲实验考核合格”为事件B1,“乙实验考核合格”为事件B2,“丙实验考核合格”为事件B3.
(1)记“理论考核中至少有两人合格”为事件C.
则P(C)=P(A1 A2
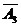 +A1
+A1 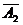 A3+
A3+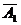 A2 A3+A1 A2 A3)
A2 A3+A1 A2 A3)
=P(A1 A2
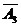 )+P(A1
)+P(A1
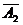 A3)+P(
A3)+P(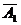 A2 A3)+P(A1
A2 A3)
A2 A3)+P(A1
A2 A3)
=0.9×0.8×0.3+0.9×0.2×0.7+0.1×0.8×0.7+0.9×0.8×0.7
=0.902
(2)记“三人该课程考核都合格”为事件D.
则P(D)=P[(A1·B1)·(A2·B2)·(A3·B3)]
=P(A1·B1)·P(A2·B2)·P(A3·B3)
=P(A1)·P(B1)·P(A2)·P(B2)·P(A3)·P(B3)
=0.9×0.8×0.8×0.8×0.7×0.9
≈0.254
所以,理论考核中至少有两人合格的概率为0.902;
这三人该课程考核都合格的概率为0.254。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com