
1.化简: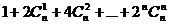
3.注意区分展开式“第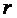 +1项的二项式系数”与“第
+1项的二项式系数”与“第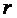 +1项的系数”.
+1项的系数”.
[例5]已知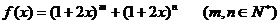 的展开式中含
的展开式中含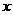 项的系数为24,求展开式中含
项的系数为24,求展开式中含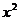 项的系数的最小值.
项的系数的最小值.
解:解法一 由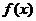 中含
中含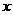 项的系数为24,可得
项的系数为24,可得
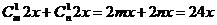 .从而,
.从而,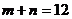 .
.
设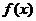 中含
中含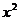 项的系数为t,则
项的系数为t,则
t=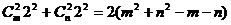 .
.
把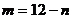 代入上式,得
代入上式,得
t=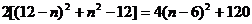 .
.
∴当n=6时,t的最小值为120,此时m=n=6.
解法二 由已知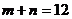 ,
,
设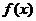 中含
中含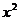 项的系数为t,则
项的系数为t,则
t=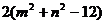 ≥2
≥2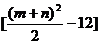 =2(72-12)=120.
=2(72-12)=120.
当且仅当m=n=6时,t有最小值120.
∴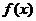 展开式中含
展开式中含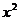 项的系数的最小值为120.
项的系数的最小值为120.
评注:构造函数法是一种常用的方法,尤其在求最值问题中应用非常广泛.
[例1]已知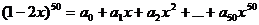 ,
,
求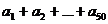 的值.
的值.
错解:由二项展开式的系数的性质可知: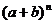 的展开式的各个二项式系数的和等于
的展开式的各个二项式系数的和等于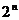 ,显然,
,显然,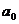 就是展开式中的
就是展开式中的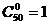 ,因此
,因此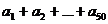 的值为
的值为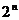 -1.
-1.
错因:上述解答忽略了 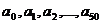 是项的系数,而不是二项式系数.
是项的系数,而不是二项式系数.
正解:由二项展开式的结构特征,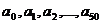 是项的系数,而不是二项式系数.观察式子特征,如果
是项的系数,而不是二项式系数.观察式子特征,如果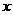 =1,则等式右边为
=1,则等式右边为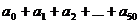 ,出现所求式子的形式,而
,出现所求式子的形式,而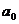 就是展开式中的
就是展开式中的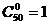 ,因此
,因此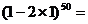
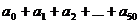 ,即
,即
1=1+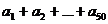 ,所以,
,所以,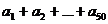 =0
=0
评注 这是二项式定理的一个典型应用-赋值法,在使用赋值法时,令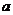 、b等于多少,应就具体问题而定,有时取“1”,有时取“-1”,或其他值.
、b等于多少,应就具体问题而定,有时取“1”,有时取“-1”,或其他值.
[例2]在多项式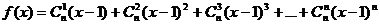 的展开式中,含
的展开式中,含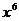 项的系数为 .
项的系数为 .
错解:原式=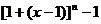 =
=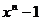
∴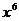 项的系数为0.
项的系数为0.
错因:忽视了n的范围,上述解法得出的结果是在n不等于6的前提下得到的,而这个条件并没有提供.
正解:原式=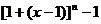 =
=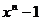
∴当n≠6时,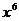 项的系数为0.
项的系数为0.
当n=6时,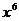 项的系数为1
项的系数为1
说明:本解法体现了逆向运用二项式定理的灵活性,应注意原式中对照二项式定理缺少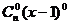 这一项.
这一项.
[例3] 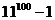 的末尾连续零的个数是 ( )
的末尾连续零的个数是 ( )
A.7 B.5 C.3 D.2
解: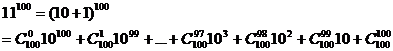
上述展开式中,最后一项为1;倒数第二项为1000;倒数第三项为495000,末尾有三个0;倒数第四项为16170000,末尾有四个0;依次前面各项末尾至少有四个0.所以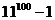 的末尾连续零的个数是3. 故选C.
的末尾连续零的个数是3. 故选C.
[例4]
已知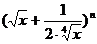 的展开式前三项中的
的展开式前三项中的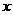 的系数成等差数列.
的系数成等差数列.
(1)求展开式中所有的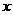 的有理项;
的有理项;
(2)求展开式中系数最大的项.
解:(1)展开式前三项的系数分别为
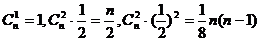 .
.
由题设可知: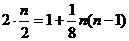
解得:n=8或n=1(舍去).
当n=8时,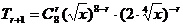 =
=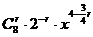 .
.
据题意,4-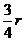 必为整数,从而可知
必为整数,从而可知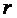 必为4的倍数,
必为4的倍数,
而0≤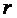 ≤8,∴
≤8,∴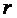 =0,4,8.
=0,4,8.
故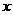 的有理项为:
的有理项为: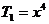 ,
,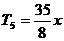 ,
,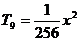 .
.
(2)设第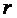 +1项的系数
+1项的系数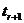 最大,显然
最大,显然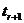 >0,
>0,
故有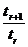 ≥1且
≥1且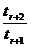 ≤1.
≤1.
∵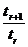 =
=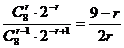 ,
,
由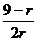 ≥1,得
≥1,得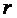 ≤3.
≤3.
∵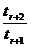 =
=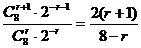 ,
,
由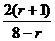 ≤1,得
≤1,得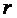 ≥2.
≥2.
∴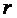 =2或
=2或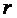 =3,所求项分别为
=3,所求项分别为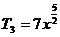 和
和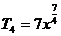 .
.
评注:1.把握住二项展开式的通项公式,是掌握二项式定理的关键,除通项公式外,还应熟练掌握二项式的指数、项数、展开式的系数间的关系、性质.
2.运用通项公式求二项展开的特定项,如求某一项,含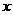 某次幂的项,常数项,有理项,系数最大的项等,一般是运用通项公式根据题意列方程,在求得n或r后,再求所需的项(要注意n和r的数值范围及大小关系).
某次幂的项,常数项,有理项,系数最大的项等,一般是运用通项公式根据题意列方程,在求得n或r后,再求所需的项(要注意n和r的数值范围及大小关系).
4.二项式奇数项系数的和等于二项式偶数项系数的和.即
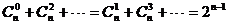
3.二项式定理的特殊表示形式
(1)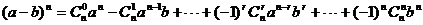 .
.
这时通项是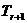 =
=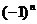
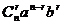 .
.
(2)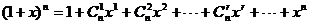 .
.
这时通项是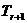 =
=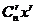 .
.
(3)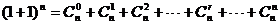 .
.
即各二项式系数的和为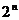 .
.
2.对二项式定理的理解和掌握,要从项数、系数、指数、通项等方面的特征去熟悉它的展开式.通项公式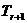 =
=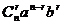 在解题时应用较多,因而显得尤其重要,但必须注意,它是
在解题时应用较多,因而显得尤其重要,但必须注意,它是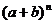 的二项展开式的第r+1项,而不是第r项.
的二项展开式的第r+1项,而不是第r项.
1.二项式定理是代数公式
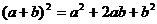 和
和
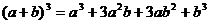
的概括和推广,它是以乘法公式为基础,以组合知识为工具,用不完全归纳法得到的.同学们可对定理的证明不作要求,但定理的内容必须充分理解.
2.二项式系数的性质:
(1)对称性.与首末两端“等距离”的两个二项式系数相等.事实上,这一性质可直接由公式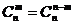 得到.
得到.
(2)增减性与最大值. 二项式系数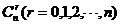 ,当r<
,当r<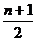 时,二项式系数是逐渐增大的.由对称性知它的后半部分是逐渐减小的,且在中间取得最大值.当n是偶数时,中间的一项取得最大值;当n是奇数时,中间的两项相等,且同时取得最大值.
时,二项式系数是逐渐增大的.由对称性知它的后半部分是逐渐减小的,且在中间取得最大值.当n是偶数时,中间的一项取得最大值;当n是奇数时,中间的两项相等,且同时取得最大值.
 (3)各二项式系数的和.
(3)各二项式系数的和.
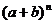 的展开式的各个二项式系数的和等于
的展开式的各个二项式系数的和等于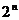 .
.
1.二项式定理: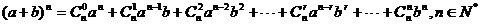
上列公式所表示的定理叫做二项式定理.
右边的多项式叫做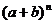 的二项展开式,它一共有n+1项.
的二项展开式,它一共有n+1项.
其中各项的系数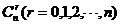 叫做二项式系数.
叫做二项式系数.
式中的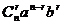 叫做二项展开式的通项,用
叫做二项展开式的通项,用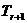 表示,
表示,
即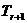 =
=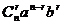 .
.
6.有6本不同的书,分给甲、乙、丙三人.
(1)甲、乙、丙三人各得2本,有多少种分法?
(2)一人得1本,一人得2本,一人得3本,有多少种分法?
(3)甲得1本,乙得2本,丙得3本,有多少种分法?
(4)平均分成三堆,每堆2本,有多少种分法?
§9.3 二项式定理
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com