
24.(本小题满分12分)
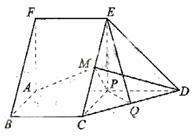
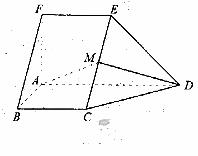 如图,在五面体ABCDEF中,FA
如图,在五面体ABCDEF中,FA 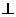 平面ABCD, AD//BC//FE,AB
平面ABCD, AD//BC//FE,AB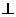 AD,M为EC的中点,AF=AB=BC=FE=
AD,M为EC的中点,AF=AB=BC=FE=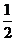 AD
AD 

(I) 求异面直线BF与DE所成的角的大小;
(II) 证明平面AMD 平面CDE;
平面CDE;
(III)求二面角A-CD-E的余弦值。 

方法一:(Ⅰ)解:由题设知,BF//CE,所以∠CED(或其
补角) 为异面直线BF与DE所成的角。设P为AD的中
 点,连结EP,PC。因为FE
点,连结EP,PC。因为FE AP,所以FA
AP,所以FA EP,同理AB
EP,同理AB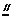 PC。
PC。
又FA⊥平面ABCD,所以EP⊥平面ABCD。而PC,AD
都在平面ABCD内,故EP⊥PC,EP⊥AD。由AB⊥AD,可
得PC⊥AD设FA=a,则EP=PC=PD=a,CD=DE=EC=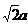 ,
,
故∠CED=60°。所以异面直线BF与DE所成的角的大小为60° 

(II)证明:因为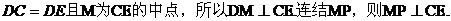
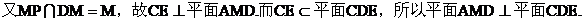 (III)
(III)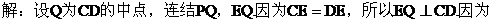
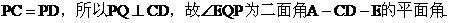
由(I)可得,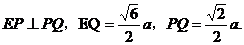
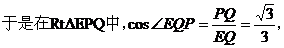


23.(本小题满分14分)
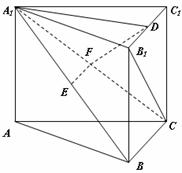
如图6,已知正方体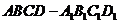 的棱长为2,点
的棱长为2,点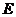 是正方形
是正方形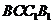 的中心,点
的中心,点
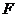 、
、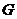 分别是棱
分别是棱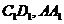 的中点.设点
的中点.设点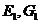 分别是点
分别是点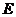 ,
,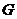 在平面
在平面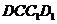 内的正投影.
内的正投影.
(1)求以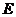 为顶点,以四边形
为顶点,以四边形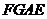 在平面
在平面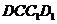 内的正投影为底面边界的棱锥的体积;
内的正投影为底面边界的棱锥的体积;
(2)证明:直线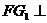 平面
平面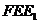 ;
;
(3)求异面直线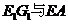 所成角的正弦值.
所成角的正弦值.
解:(1)依题作点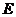 、
、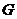 在平面
在平面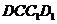 内的正投影
内的正投影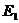 、
、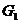 ,则
,则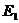 、
、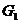 分别为
分别为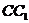 、
、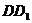 的中点,连结
的中点,连结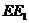 、
、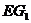 、
、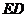 、
、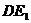 ,则所求为四棱锥
,则所求为四棱锥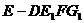 的体积,其底面
的体积,其底面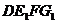 面积为
面积为
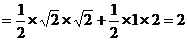 ,
,
又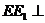 面
面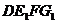 ,
,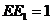 ,∴
,∴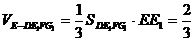 .
.
(2)以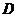 为坐标原点,
为坐标原点,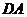 、
、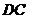 、
、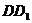 所在直线分别作
所在直线分别作 轴,
轴,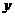 轴,
轴,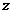 轴,得
轴,得 、
、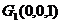 ,又
,又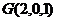 ,
,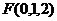 ,
,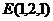 ,则
,则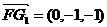 ,
,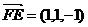 ,
,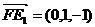 ,
,
∴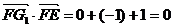 ,
,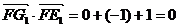 ,即
,即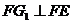 ,
,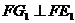 ,
,
又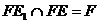 ,∴
,∴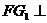 平面
平面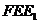 .
.
(3)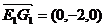 ,
,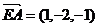 ,则
,则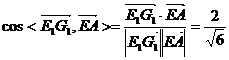 ,设异面直线
,设异面直线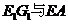 所成角为
所成角为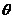 ,则
,则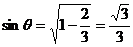 .
.
22. (本小题满分14分)
(本小题满分14分)
如图,在直三棱柱 中,
中,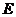 、
、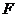 分别是
分别是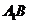 、
、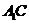 的中
的中
点,点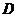 在
在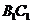 上,
上,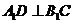 。
。
求证:(1)EF∥平面ABC; 
(2)平面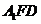
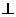 平面
平面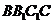 .
.
[解析] 本小题主要考查直线与平面、平面与平面得位置关系,考查
空间想象能力、推理论证能力。满分14分。

21.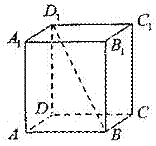 如图,若正四棱柱
如图,若正四棱柱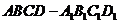 的底面连长为2,高 为
的底面连长为2,高 为
4,则异面直线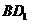 与AD所成角的大小是______________(结果
与AD所成角的大小是______________(结果
用反三角函数表示).
答案 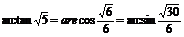
三、解答题
20. 如图,已知正三棱柱
如图,已知正三棱柱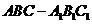 的各条棱长都相等,
的各条棱长都相等,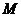 是侧
是侧
棱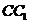 的中点,则异面直线
的中点,则异面直线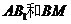 所成的角的大小
所成的角的大小
是 。
答案 

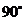
19.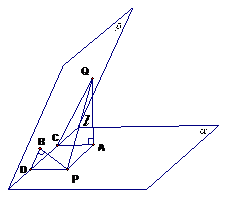 已知二面角α-l-β为
已知二面角α-l-β为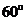 ,动点P、Q分别在面α、β内,P到β的距离为
,动点P、Q分别在面α、β内,P到β的距离为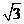 ,Q到α的距离为
,Q到α的距离为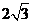 ,则P、Q两点之间距离的最小值为( C )
,则P、Q两点之间距离的最小值为( C )
(A) (B)2
(C)
(B)2
(C) 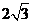 (D)4
(D)4 

解:如图分别作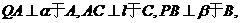
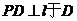 ,连
,连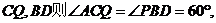
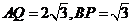 ,
,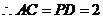
又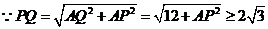
当且仅当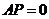 ,即
,即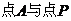 重合时取最小值。故答案选C。
重合时取最小值。故答案选C。 

18.已知三棱柱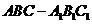 的侧棱与底面边长都相等,
的侧棱与底面边长都相等,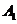 在底面
在底面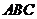 上的射影为
上的射影为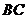 的
的
中点,则异面直线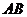 与
与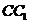 所成的角的余弦值为( D )
所成的角的余弦值为( D )
(A)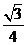 (B)
(B)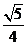 (C)
(C)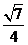 (D)
(D) 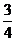


解:设 的中点为D,连结
的中点为D,连结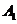 D,AD,易知
D,AD,易知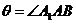 即为异面直线
即为异面直线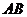 与
与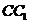 所 成的角,由三角余弦定理,易知
所 成的角,由三角余弦定理,易知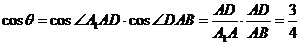 .故选D
.故选D 

17.对于四面体ABCD,下列命题正确的是_________
(写出所有正确命题的编号)。 

1相对棱AB与CD所在的直线异面;
2由顶点A作四面体的高,其垂足是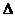 BCD的三条高线的交点;
BCD的三条高线的交点;
3若分别作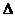 ABC和
ABC和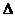 ABD的边AB上的高,则这两条高所在直线异面;
ABD的边AB上的高,则这两条高所在直线异面;
4分别作三组相对棱中点的连线,所得的三条线段相交于一点;
5最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱。
[解析]①④⑤
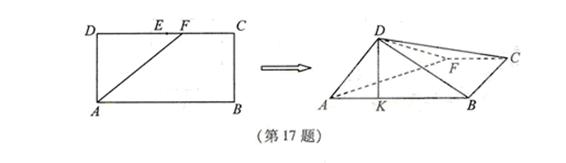
16.如图,在长方形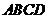 中,
中,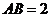 ,
,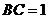 ,
,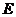 为
为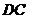 的中点,
的中点,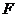 为线段
为线段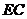 (端
(端
点除外)上一动点.现将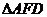 沿
沿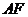 折起,使平面
折起,使平面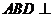 平面
平面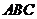 .在平面
.在平面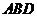 内过点
内过点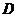 作
作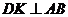 ,
,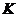 为垂足.设
为垂足.设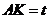 ,则
,则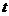 的取值范围是
.
的取值范围是
.
答案: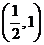
[解析]此题的破解可采用二个极端位置法,即对于F位于DC的中点时,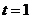 ,随着 F点到C点时,因
,随着 F点到C点时,因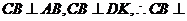 平面
平面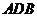 ,即有
,即有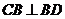 ,对于
,对于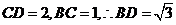 ,又
,又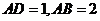 ,因此有
,因此有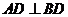 ,则有
,则有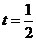 ,因此
,因此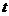 的取值范围是
的取值范围是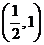


15.如图,已知六棱锥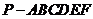 的底面是正六边形,
的底面是正六边形,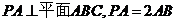 ,则
,则
下列结论正确的是
A.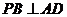 B.平面
B.平面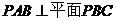


C. 直线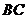 ∥平面
∥平面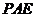 D.
D.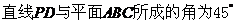
答案 D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com