
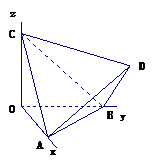
14.如图,正四面体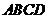 的顶点
的顶点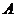 ,
,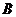 ,
,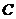 分别在两两垂直的三条射线
分别在两两垂直的三条射线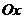 ,
,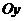 ,
,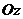 上,则在下列命题中,错误的为
上,则在下列命题中,错误的为
 A.
A.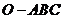 是正三棱锥
是正三棱锥
B.直线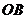 ∥平面
∥平面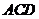
C.直线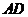 与
与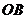 所成的角是
所成的角是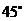
D.二面角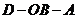 为
为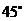


 答案 B
答案 B
13.平面六面体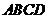 -
- 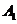
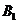
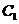
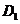 中,既与
中,既与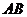 共面也与
共面也与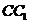 共面的棱的条数为[ C ]
共面的棱的条数为[ C ]
A.3 B. 4 C.5 D. 6


12.正方体ABCD-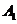
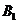
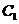
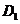 的棱上到异面直线AB,C
的棱上到异面直线AB,C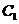 的
的
距离相等的点的个数为(C)
A.2
B.3 C.
4
D. 5 

11.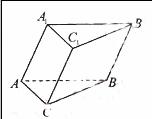 如图,在三棱柱ABC-A1B1C1中,∠ACB=900,∠ACC1=600,∠BCC1=450,侧棱CC1的长为1,则
如图,在三棱柱ABC-A1B1C1中,∠ACB=900,∠ACC1=600,∠BCC1=450,侧棱CC1的长为1,则
该三棱柱的高等于
A.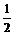 B.
B.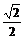
C.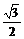
 D.
D.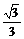


A
10.在正四棱柱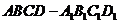 中,顶点
中,顶点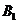 到对角线
到对角线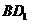 和到平面
和到平面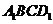 的距离分别为
的距离分别为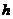 和
和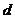 ,则下列命题中正确的是
,则下列命题中正确的是
A.若侧棱的长小于底面的边长,则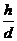 的取值范围为(0,1)
的取值范围为(0,1)
B.若侧棱的长小于底面的边长,则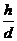 的取值范围为
的取值范围为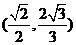
C.若侧棱的长大于底面的边长,则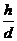 的取值范围为
的取值范围为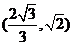


D.若侧棱的长大于底面的边长,则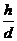 的取值范围为
的取值范围为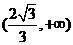
C
9.已知二面角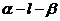 的大小为
的大小为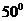 ,
,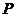 为空间中任意一点,则过点
为空间中任意一点,则过点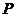 且与平面
且与平面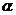 和
和
平面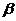 所成的角都是
所成的角都是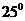 的直线的条数为( )
的直线的条数为( ) 

A.2 B.3 C.4 D.5 

答案 B
8.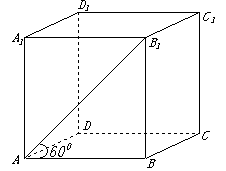 若正四棱柱
若正四棱柱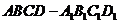 的底面边长为1,
的底面边长为1,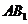 与底面
与底面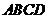 成60°角,则
成60°角,则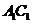
到底面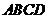
的距离为 ( )
A. B.1
B.1
C.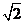 D.
D.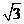
[答案]D
[解析]本题主要考查正四棱柱的概念、
直线与平面所成的角以及直线与平面的距离等概念. (第4题解答图)
属于基础知识、基本运算的考查.
依题意,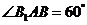 ,如图,
,如图,
 ,故选D.
,故选D.
7. 已知正四棱柱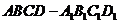 中,
中,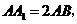
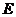 为
为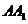 中点,则异面直线
中点,则异面直线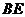 与
与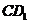
所成的角的余弦值为
A. 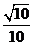 B.
B.
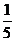 C.
C.
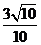 D.
D.
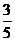
解:令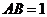 则
则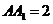 ,连
,连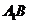
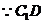 ∥
∥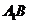
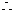 异面直线
异面直线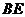 与
与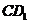 所成的角即
所成的角即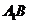
与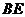 所成的角。在
所成的角。在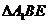 中由余弦定理易得
中由余弦定理易得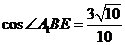 。故选C
。故选C
6.设m,n是平面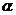 内的两条不同直线,
内的两条不同直线,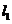 ,
,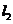 是平面
是平面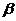 内的两条相交直线,则
内的两条相交直线,则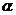 //
// 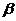 的
的
一个充分而不必要条件是


A.m // 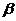 且l //
且l // 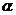 B.
m // l
且n // l
B.
m // l
且n // l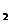
C. m // 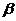 且n //
且n // 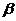 D.
m //
D.
m // 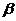 且n // l
且n // l
[答案]:B
[解析]若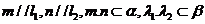 ,则可得
,则可得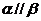 .若
.若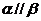 则存在
则存在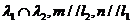
5.C [命题意图]此题主要考查立体几何的线面、面面的位置关系,通过对平行和垂直的考查,充分调动了立体几何中的基本元素关系.
[解析]对于A、B、D均可能出现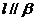 ,而对于C是正确的.
,而对于C是正确的. 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com