
3、介词+关系代词which, whom等,不能用that, who。
2、先行词是表示时间或地点的名词时,用关系副词when,where还是用关系副词which ,that。
1、关系代词who(m)、which、that的选用和省略。
1.4.2微积分基本定理
|
学习目标: 1.通过实例,直观了解微积分基本定理的含义,会用牛顿-莱布尼兹公式求简单的定积分 2.通过实例体会用微积分基本定理求定积分的方法 3.通过微积分基本定理的学习,体会事物间的相互转化、对立统一的辩证关系,培养学生辩证唯物主义观点,提高理性思维能力 学习重点难点: 通过探究变速直线运动物体的速度与位移的关系,使学生直观了解微积分基本定理的含义,并能正确运用基本定理计算简单的定积分 自主学习: 一、知识回顾: 定积分的概念及用定义计算 二、新课探究 我们讲过用定积分定义计算定积分,但其计算过程比较复杂,所以不是求定积分的一般方法。我们必须寻求计算定积分的新方法,也是比较一般的方法。 变速直线运动中位置函数与速度函数之间的联系 设一物体沿直线作变速运动,在时刻t时物体所在位置为S(t),速度为v(t)( 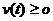 ), ),则物体在时间间隔 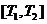 内经过的路程可用速度函数表示为 内经过的路程可用速度函数表示为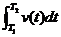 。 。另一方面,这段路程还可以通过位置函数S(t)在 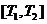 上的增量 上的增量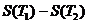 来表达,即 来表达,即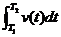 = =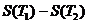 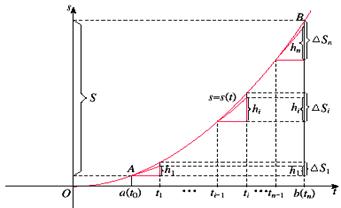 而 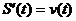 。 。对于一般函数 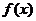 ,设 ,设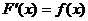 ,是否也有 ,是否也有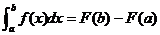 若上式成立,我们就找到了用 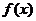 的原函数(即满足 的原函数(即满足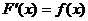 )的数值差 )的数值差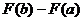 来计算 来计算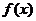 在 在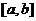 上的定积分的方法。 上的定积分的方法。注:1:定理 如果函数 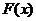 是 是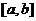 上的连续函数 上的连续函数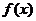 的任意一个原函数,则 的任意一个原函数,则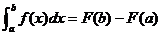 证明:因为 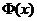 = =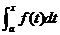 与 与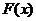 都是 都是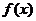 的原函数,故 的原函数,故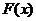 - -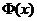 =C( =C(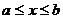 )其中C为某一常数。 )其中C为某一常数。令 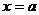 得 得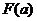 - -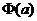 =C,且 =C,且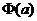 = =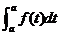 =0 =0即有C= 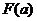 ,故 ,故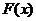 = =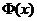 + +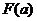 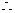 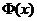 = =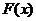 - -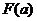 = =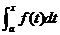 令 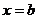 ,有 ,有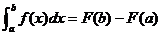 此处并不要求学生理解证明的过程 为了方便起见,还常用 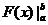 表示 表示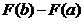 ,即 ,即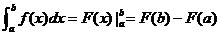 该式称之为微积分基本公式或牛顿-莱布尼兹公式。它指出了求连续函数定积分的一般方法,把求定积分的问题,转化成求原函数的问题,是微分学与积分学之间联系的桥梁。 它不仅揭示了导数和定积分之间的内在联系,同时也提供计算定积分的一种有效方法,为后面的学习奠定了基础。因此它在教材中处于极其重要的地位,起到了承上启下的作用,不仅如此,它甚至给微积分学的发展带来了深远的影响,是微积分学中最重要最辉煌的成果。 三、例题解析: 例1.计算下列定积分: (1) 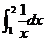 ; (2) ; (2)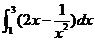 。 。解:(1)因为 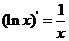 ,所以 ,所以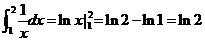 。 。(2))因为 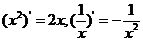 , ,所以 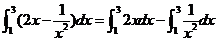 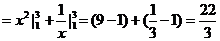 。 。例2.计算下列定积分: 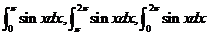 。 。由计算结果你能发现什么结论?试利用曲边梯形的面积表示所发现的结论。 解:因为 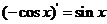 , ,所以 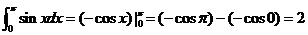 , ,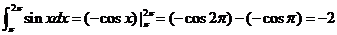 , ,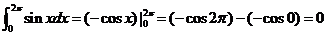 . . 可以发现,定积分的值可能取正值也可能取负值,还可能是0: ( l )当对应的曲边梯形位于 x 轴上方时(图1.6一3 ) ,定积分的值取正值,且等于曲边梯形的面积; 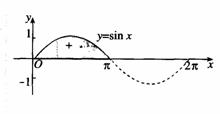 图1 . 6 一 3 ( 2 ) (2)当对应的曲边梯形位于 x 轴下方时(图 1 . 6 一 4 ) ,定积分的值取负值,且等于曲边梯形的面积的相反数; 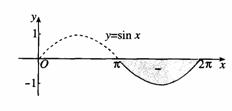 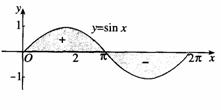 ( 3)当位于 x 轴上方的曲边梯形面积等于位于 x 轴下方的曲边梯形面积时,定积分的值为0(图 1 . 6 一 5 ) ,且等于位于 x 轴上方的曲边梯形面积减去位于 x 轴下方的曲边梯形面积. 例3.汽车以每小时32公里速度行驶,到某处需要减速停车。设汽车以等减速度 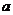 =1.8米/秒2刹车,问从开始刹车到停车,汽车走了多少距离? =1.8米/秒2刹车,问从开始刹车到停车,汽车走了多少距离?解:首先要求出从刹车开始到停车经过了多少时间。当t=0时,汽车速度 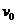 =32公里/小时= =32公里/小时=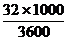 米/秒 米/秒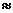 8.88米/秒,刹车后汽车减速行驶,其速度为 8.88米/秒,刹车后汽车减速行驶,其速度为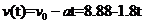 当汽车停住时,速度 当汽车停住时,速度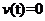 ,故从 ,故从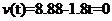 解得 解得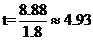 秒 秒于是在这段时间内,汽车所走过的距离是 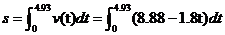 = =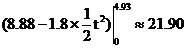 米,即在刹车后,汽车需走过21.90米才能停住. 米,即在刹车后,汽车需走过21.90米才能停住.微积分基本定理揭示了导数和定积分之间的内在联系,同时它也提供了计算定积分的一种有效方法.微积分基本定理是微积分学中最重要的定理,它使微积分学蓬勃发展起来,成为一门影响深远的学科,可以毫不夸张地说,微积分基本定理是微积分中最重要、最辉煌的成果. 课堂巩固: 1.曲线 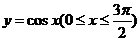 与坐标轴围成的面积是 与坐标轴围成的面积是A.4 B. 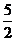 C.3 D.2 C.3 D.22.下列积分不正确的是 A、 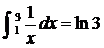 B、 B、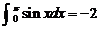 C、 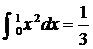 D、 D、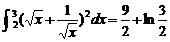 3.计算 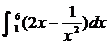 =_________ =_________4. 计算 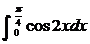 =____________ =____________归纳反思: 合作探究: 1.求抛物线 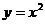 与直线x+y=2所围图形的面积 与直线x+y=2所围图形的面积2.求由曲线 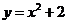 与 与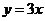 , ,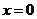 , ,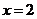 所围成的平面图形的面积 所围成的平面图形的面积 |
|
33. [江苏省刘国钧中学2008-2009学年第一学期期末复习测试(2)文科第17题]
某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:
|
推销员编号 |
1 |
2 |
3 |
4 |
5 |
工作年限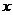 /年 /年 |
3 |
5 |
6 |
7 |
9 |
推销金额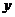 /万元 /万元 |
2 |
3 |
3 |
4 |
5 |
(Ⅰ)求年推销金额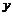 与工作年限x之间的相关系数;
与工作年限x之间的相关系数;
(Ⅱ)求年推销金额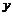 关于工作年限
关于工作年限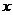 的线性回归方程;
的线性回归方程;
(Ⅲ)若第6名推销员的工作年限为11年,试估计他的年推销金额.
(参考数据:;由检验水平0.01及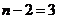 ,查表得
,查表得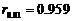 .)
.)
参考公式:
线性相关系数公式: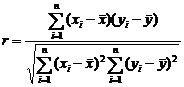
线性回归方程系数公式: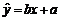 ,其中
,其中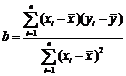 ,
,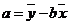 .
.
32.(2008广州调研文)已知射手甲射击一次,命中9环(含9环)以上的概率为0.56,命中8环的概率为0.22,命中7环的概率为0.12.
(1)求甲射击一次,命中不足8环的概率;
(2)求甲射击一次,至少命中7环的概率.
31、[天津市汉沽一中2008-2009学年度高三第四次月考试题数学(文科)第16题](本小题满分12分)
某班甲、乙两学生的高考备考成绩如下:
甲: 512 554 528 549 536 556 534 541 522 538
乙:515 558 521 543 532 559 536 548 527 531
(1)用茎叶图表示两学生的成绩;
(2)分别求两学生成绩的中位数和平均分.
30.[浙江省五校2009届高三第一次联考数学(文科)试题卷第19题](本小题满分14分)
把一根长度为6的铁丝截成3段.
(Ⅰ)若三段的长度均为整数,求能构成三角形的概率;
(Ⅱ)若截成任意长度的三段,求能构成三角形的概率.
29.[宁夏区银川一中2009届高三年级第四次月考数 学 试 题(文科)第20题](本小题满分12分)
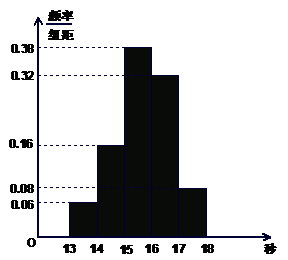 某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:每一组
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:每一组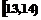 ;第二组
;第二组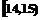 ……第五组
……第五组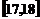 .下图是按上述分组方法得到的频率分布直方图.
.下图是按上述分组方法得到的频率分布直方图.
(I)若成绩大于或等于14秒且小于16秒
认为良好,求该班在这次百米测试中
成绩良好的人数;
(II)设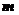 、
、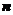 表示该班某两位同学的百米
表示该班某两位同学的百米
测试成绩,且已知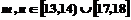 .
.
求事件“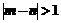 ”的概率.
”的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com