3.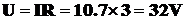电流表和电压表的读数I=10.7A

2.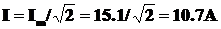　 有效值为

转过90⁰的过程中电阻R上产生的热量为

Q=I² R t= I² R T/4=10.7J　

感应电流的平均值为

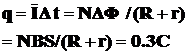转过90⁰的过程中通过导线横截面的电量为

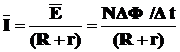
3.　　 　

解：从中性面开始计时有 e=E _m sin ω t ，其中E_m = NB ω S，

ω=2πn=2 π ×480/60=16π，∴ E_m = NBωS =60.3V，I_m = E_m /(R+r)=15.1A

注意到从开始转动时产生的感应电流沿dcbad方向，与规定方向相反，为负值。∴i 　= - I_m sinω t= -15.1 sin 16πt　 (A)

T=2π/ω=1/8 s

图线如图示

4.从图示位置转过180°过程中

的平均感应电动势

3.电流表和电压表的读数

2.　　 线圈从图示位置转过1/4 转的过程中,

电阻R上产生的热量和通过导线截面

的电量

1.　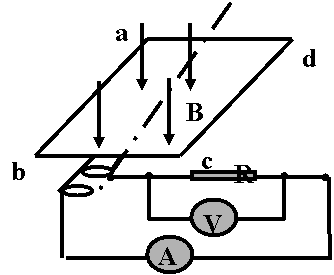　 若线圈从图示位置开始计时,沿abcd流动

的方向为正方向,画出交流电流的图象.

10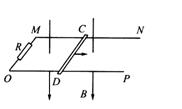．如图所示，电阻不计的平行金属导轨MN和OP水平放置，MO间接有阻值为R的电阻，导轨相距为d，其间有竖直向下的匀强磁场，磁感强度为B．质量为m、电阻为r的导体棒CD垂直于导轨放置，并接触良好．用平行于MN的恒力F向右拉动CD，CD受恒定的摩擦阻力．f，已知F>f．问：

　(1)CD运动的最大速度是多少?

　(2)当CD达到最大速度后，电阻R消耗的电功率是多少?

(3)当CD的速度是最大速度的1/3时，CD的加速度是多少?

解析：(1)以金属棒为研究对象，当CD受力：F=F_A+f时，CD速度最大，

即：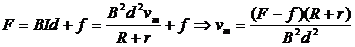

(2)CD棒产生的感应电动势为：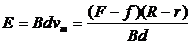

回路中产生的感应电流为：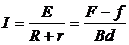

则R中消耗的电功率为：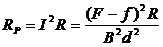

(3)当CD速度为最大速度的1/3即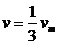时，CD中的电流为最大值的1/3即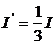则CD棒所受的安培力为：

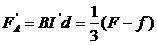
　CD棒的加速度为：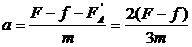

9、如图所示，两根足够长的直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上，两导轨间距为L，M、P两点间接有阻值为R的电阻．一根质量为m的均匀直金属杆ab放在两导轨上，并与导轨垂直整套装置处于磁感应强度为B的匀强磁场中，磁场方向垂直斜面向下，导轨和金属杆的电阻可忽略·让ab杆沿导轨由静止开始下滑，导轨和金属杆接触良好，不计它们之间的摩擦．

　　 (1)由b向a方向看到的装置如图1 5-2所示，请在此图中画出ab杆下滑过程中某时刻的受力示意图；

　　 (2)在加速下滑过程中，当杆ab的速度大小为v时，求此时ab杆中的电流及其加速度的大小；

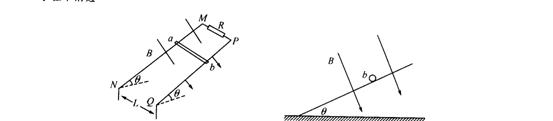　　 (3)求在下滑过程中，ab杆可以达到的速度最大值．

解：(1)重力mg，竖直向下；支撑力N，，垂直斜面向上；安培力F，沿斜面向上．

(2)当ab杆速度为v时，感应电动势E=BLv，此时电路电流

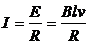
杆受到安培力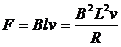

根据牛顿运动定律，有：　　　　

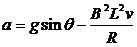
(3)当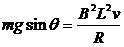时，ab杆达到最大速度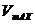

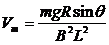
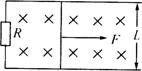
8、水平面上两根足够长的金属导轨平行固定放置，间距为L，一端通过导线与阻值为R的电阻连接；导轨上放一质量为m的金属杆(见图)，金属杆与导轨的电阻不计；均匀磁场竖直向下．用与导轨平行的恒定力F作用在金属杆上，杆最终将做匀速运动．当改拉力的大小时，相对应的匀速运动速度v也会改变，v和F的关系如图 (取重力加速度g=10m／s ²)

(1)金属杆在匀速运动之前做作什么运动?

(2)若m＝0.5 kg，L＝0.5 m，R＝0.5 Ω，磁感应强度B为多大?

(3)由ν－F图线的截距可求得什么物理量?其值为多少?

解： (1)变速运动(或变加速运动、加速度减小的加速运动，加速运动)．

(2)感应电动势E-vBL，感应电流I=E/R

安培力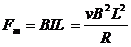

由图可知金属杆受拉力、安培力和阻力作用，匀速时合力为零

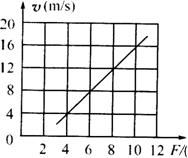
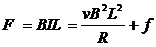
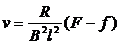
由图线可以得到直线的斜率k=2

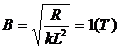
(3)由直线的截距可以求得金属杆受到的阻力f，　　　 f=2(N)．

若金属杆受到的阻力仅为动摩擦力，由截距可求得动摩擦因数　　μ=0.4