
5、全称命题与特称命题:
短语“所有”在陈述中表示所述事物的全体,逻辑中通常叫做全称量词,并用符号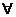 表示。含有全体量词的命题,叫做全称命题。
表示。含有全体量词的命题,叫做全称命题。
短语“有一个”或“有些”或“至少有一个”在陈述中表示所述事物的个体或部分,逻辑中通常叫做存在量词,并用符号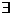 表示,含有存在量词的命题,叫做存在性命题。
表示,含有存在量词的命题,叫做存在性命题。
全称命题p: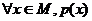 ;
全称命题p的否定
;
全称命题p的否定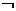 p:
p: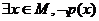 。
。
特称命题p: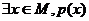 ;
特称命题p的否定
;
特称命题p的否定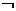 p:
p: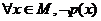 ;
;
考前寄语:①先易后难,先熟后生;②一慢一快:审题要慢,做题要快;③不能小题难做,小题大做,而要小题小做,小题巧做;④我易人易我不大意,我难人难我不畏难;⑤考试不怕题不会,就怕会题做不对;⑥基础题拿满分,中档题拿足分,难题力争多得分,似曾相识题力争不失分;⑦对数学解题有困难的考生的建议:立足中下题目,力争高上水平,有时“放弃”是一种策略.
4、充要条件
由条件可推出结论,条件是结论成立的充分条件;由结论可推出条件,则条件是结论成立的必要条件。
3、逻辑联结词:






 ⑴且(and) :命题形式 p
⑴且(and) :命题形式 p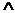 q; p q p
q; p q p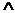 q p
q p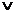 q
q 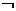 p
p
 ⑵或(or):
命题形式 p
⑵或(or):
命题形式 p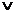 q; 真 真 真 真 假
q; 真 真 真 真 假
 ⑶非(not):命题形式
⑶非(not):命题形式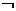 p .
真
假 假 真 假
p .
真
假 假 真 假
 假 真 假 真 真
假 真 假 真 真
 假 假 假 假 真
假 假 假 假 真

“或命题”的真假特点是“一真即真,要假全假”;
“且命题”的真假特点是“一假即假,要真全真”;
“非命题”的真假特点是“一真一假”
2、注意命题的否定与否命题的区别:命题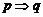 否定形式是
否定形式是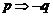 ;否命题是
;否命题是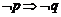 .命题“
.命题“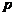 或
或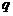 ”的否定是“
”的否定是“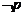 且
且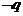 ”;“
”;“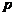 且
且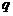 ”的否定是“
”的否定是“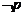 或
或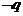 ”.
”.
1、四种命题:
⑴原命题:若p则q;⑵逆命题:若q则p;⑶否命题:若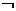 p则
p则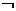 q;⑷逆否命题:若
q;⑷逆否命题:若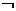 q则
q则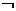 p
p
注:1、原命题与逆否命题等价;逆命题与否命题等价。判断命题真假时注意转化。
5.导数的应用:
(1)利用导数判断函数的单调性:设函数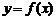 在某个区间内可导,如果
在某个区间内可导,如果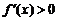 ,那么
,那么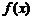 为增函数;如果
为增函数;如果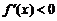 ,那么
,那么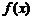 为减函数;
为减函数;
注意:如果已知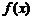 为减函数求字母取值范围,那么不等式
为减函数求字母取值范围,那么不等式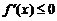 恒成立。
恒成立。
(2)求极值的步骤:
①求导数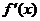 ;
;
②求方程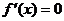 的根;
的根;
③列表:检验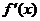 在方程
在方程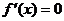 根的左右的符号,如果左正右负,那么函数
根的左右的符号,如果左正右负,那么函数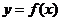 在这个根处取得极大值;如果左负右正,那么函数
在这个根处取得极大值;如果左负右正,那么函数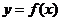 在这个根处取得极小值;
在这个根处取得极小值;
(3)求可导函数最大值与最小值的步骤:
ⅰ求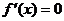 的根;
ⅱ把根与区间端点函数值比较,最大的为最大值,最小的是最小值。
的根;
ⅱ把根与区间端点函数值比较,最大的为最大值,最小的是最小值。
4.导数的四则运算法则: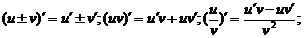
3.常见函数的导数公式: ①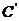
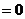 ;②
;②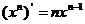 ;③
;③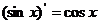
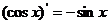 ;
;
⑤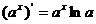 ;⑥
;⑥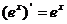 ;⑦
;⑦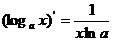 ;⑧
;⑧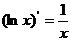 。
。
2. 导数的几何物理意义:曲线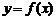 在点
在点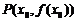 处切线的斜率
处切线的斜率
①k=f/(x0)表示过曲线y=f(x)上P(x0,f(x0))切线斜率。V=s/(t) 表示即时速度。a=v/(t) 表示加速度。
1、导数的定义: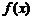 在点
在点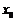 处的导数记作
处的导数记作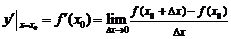 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com