
15.(坐标系与参数方程选做题)
直线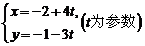 被圆
被圆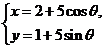 (
(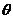 为参数)
为参数)
所截得的弦长为 .
12.坐标系与参数方程
GZ-T 14.(坐标系与参数方程选讲选做题)
在直角坐标系中圆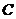 的参数方程为
的参数方程为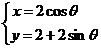 (
(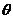 为参数),
为参数),
以原点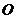 为极点,以
为极点,以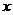 轴正半轴为极轴建立极坐标系,则圆
轴正半轴为极轴建立极坐标系,则圆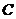 的圆心极坐标为_________.
的圆心极坐标为_________.
GZ-1 13.(坐标系与参数方程选做题)
在极坐标系中,直线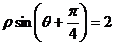 被圆
被圆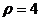 截得的弦长为__
.
截得的弦长为__
.
12.在平面内有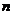
 ≥
≥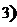 条直线,其中任何两条不平行,任何三条不过同一点,
条直线,其中任何两条不平行,任何三条不过同一点,
若这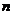 条直线把平面分成
条直线把平面分成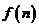 个平面区域,
个平面区域,
则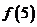 的值是
,
的值是
,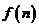 的表达式是 .
的表达式是 .
GZ-2 18.(本小题满分14分)
已知等比数列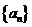 的前
的前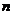 项和为
项和为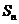 ,若
,若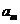 ,
,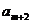 ,
,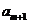
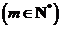 成等差数列,
成等差数列,
试判断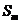 ,
,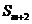 ,
,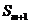 是否成等差数列,并证明你的结论.
是否成等差数列,并证明你的结论.
GZ-2 19.(本小题满分14分)
一个口袋中装有2个白球和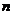 个红球(
个红球(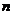 ≥2且
≥2且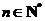 ),
),
每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),
若摸出的两个球颜色相同为中奖,否则为不中奖.
(1)试用含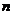 的代数式表示一次摸球中奖的概率
的代数式表示一次摸球中奖的概率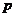 ;
;
(2)若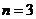 ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;
(3)记三次摸球恰有一次中奖的概率为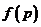 ,当
,当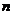 为何值时,
为何值时,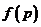 最大?
最大?
11.推理与证明
GZ-2
10.计数原理
GZ-T 10. 在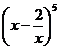 的二项展开式中,x3的系数是_______________.(用数字作答)
的二项展开式中,x3的系数是_______________.(用数字作答)
GZ-1 7.在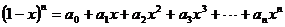 中,
中,
若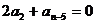 ,则自然数
,则自然数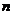 的值是
的值是
A.7 B.8 C.9 D.10
GZ-2 7.现有4种不同颜色要对如图1所示的四个部分进行着色,
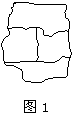 要求有公共边界的两块不能用同一种颜色,则不同的着色方法共有
要求有公共边界的两块不能用同一种颜色,则不同的着色方法共有
A.24种 B.30种 C.36种 D.48种
9.复数
GZ-T 1.已知i为虚数单位,则(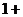 i)(
i)(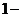 i)=
i)=
A.0 B.1 C.2 D.2i
GZ-1 2.已知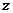
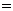 i(1
i(1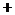 i)(i为虚数单位),则复数
i)(i为虚数单位),则复数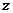 在复平面上所对应的点位于
在复平面上所对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
GZ-2 1.如果复数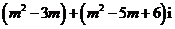 是纯虚数,则实数
是纯虚数,则实数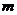 的值为
的值为
A.0 B.2 C.0或3 D.2或3
7.平面解析几何
GZ-T 4.经过圆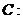
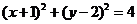 的圆心且斜率为1的直线方程为
的圆心且斜率为1的直线方程为
A.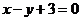 B.
B.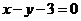 C.
C.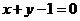 D.
D.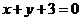
GZ-T 8. 已知抛物线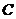 的方程为
的方程为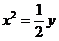 ,
,
过点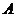
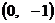 和点
和点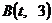 的直线与抛物线
的直线与抛物线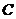 没有公共点,
没有公共点,
则实数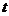 的取值范围是
的取值范围是
A. 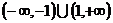 B.
B. 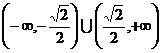
C. 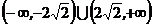 D.
D. 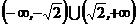
GZ-T 12. 已知变量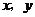 满足约束条件
满足约束条件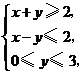
若目标函数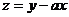 仅在点
仅在点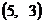 处取得最小值, 则实数
处取得最小值, 则实数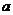 的取值范围为 .
的取值范围为 .
GZ-T 19. (本小题满分14分)
设椭圆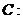
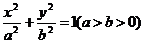 的离心率为
的离心率为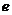 =
=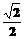 ,
,
点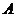 是椭圆上的一点,且点
是椭圆上的一点,且点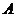 到椭圆
到椭圆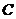 两焦点的距离之和为4.
两焦点的距离之和为4.
(1)求椭圆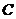 的方程;
的方程;
(2)椭圆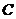 上一动点
上一动点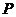
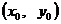 关于直线
关于直线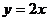 的对称点为
的对称点为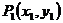 ,
,
求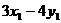 的取值范围.
的取值范围.
GZ-1 4.已知过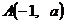 、
、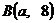 两点的直线与直线
两点的直线与直线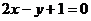 平行,则
平行,则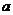 的值为
的值为
A. 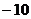 B.
B. 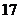 C.
C.
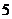 D.
D. 
GZ-1 20.(本小题满分14分)
已知动圆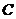 过点
过点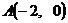 ,且与圆
,且与圆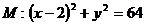 相内切.
相内切.
(1)求动圆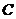 的圆心的轨迹方程;
的圆心的轨迹方程;
(2)设直线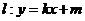 (其中
(其中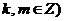 与(1)中所求轨迹交于不同两点
与(1)中所求轨迹交于不同两点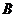 ,D,
,D,
与双曲线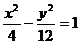 交于不同两点
交于不同两点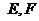 ,问是否存在直线
,问是否存在直线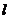 ,使得向量
,使得向量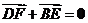 ,
,
若存在,指出这样的直线有多少条?若不存在,请说明理由.
GZ-2
5.已知点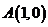 ,直线
,直线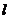 :
: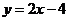 ,点
,点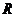 是直线
是直线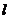 上的一点,
上的一点,
若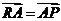 ,则点
,则点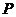 的轨迹方程为
的轨迹方程为
A.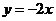 B.
B.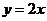 C.
C.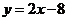 D.
D.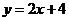
GZ-2 21.(本小题满分14分)
已知双曲线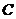 :
: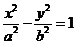
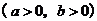 的离心率为
的离心率为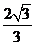 ,
,
左、右焦点分别为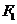 、
、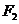 ,在双曲线
,在双曲线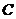 上有一点
上有一点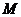 ,使
,使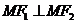 ,
,
且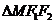 的面积为
的面积为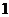 .
.
(1)求双曲线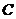 的方程;
的方程;
(2)过点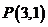 的动直线
的动直线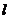 与双曲线
与双曲线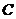 的左、右两支分别相交于两点
的左、右两支分别相交于两点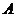 、
、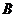 ,
,
在线段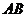 上取异于
上取异于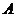 、
、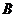 的点
的点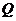 ,满足
,满足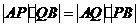 .
.
证明:点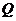 总在某定直线上.
总在某定直线上.
6.立体几何
GZ-T 7.图2为一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,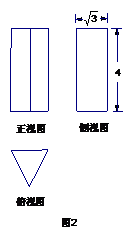 则该几何体的侧面积为
则该几何体的侧面积为
A.6 B.12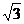 C.24 D.32
C.24 D.32
GZ-T 18.(本小题满分14分)
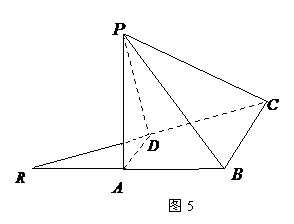
如图5,已知等腰直角三角形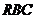 ,其中∠
,其中∠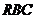 =90º,
=90º,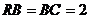 .
.
点A、D分别是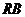 、
、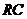 的中点,现将△
的中点,现将△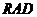 沿着边
沿着边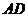 折起到△
折起到△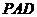 位置,
位置,
 使
使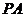 ⊥
⊥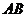 ,连结
,连结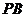 、
、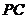 .
.
(1)求证: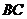 ⊥
⊥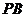 ;
;
(2)求二面角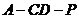 的平面角的余弦值.
的平面角的余弦值.
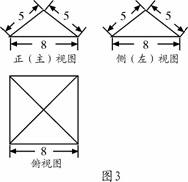
GZ-1 11.一个几何体的三视图及其尺寸(单位:cm)如图3所示,
则该几何体的侧面积为
cm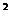 .
.
GZ-1 18. (本小题满分14分)
如图4, 在三棱锥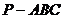 中,
中,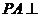 平面
平面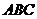 ,
,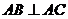 ,
,
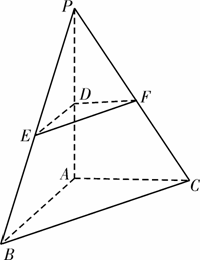
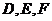 分别是棱
分别是棱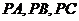 的中点,连接
的中点,连接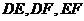 .
.
(1)求证: 平面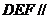 平面
平面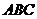 ;
;
(2)若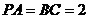 , 当三棱锥
, 当三棱锥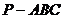 的体积最大时,
的体积最大时,
求二面角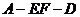 的平面角的余弦值.
的平面角的余弦值.
图4
GZ-2 8.设直线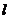 与球
与球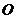 有且只有一个公共点
有且只有一个公共点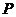 ,
,
从直线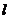 出发的两个半平面
出发的两个半平面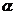 、
、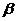 截球
截球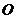 的两个截面圆的半径分别为
的两个截面圆的半径分别为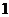 和
和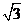 ,
,
二面角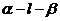 的平面角为
的平面角为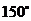 ,则球
,则球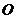 的表面积为
的表面积为
A.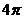 B.
B.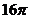 C.
C.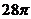 D.
D.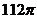
GZ-T 9.在空间直角坐标系中,
以点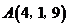 ,
,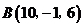 ,
,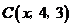 为顶点的
为顶点的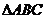 是
是
以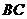 为斜边的等腰直角三角形,则实数
为斜边的等腰直角三角形,则实数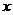 的值为 .
的值为 .
GZ-2 17.(本小题满分12分)
在长方体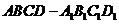 中,
中,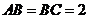 ,
,
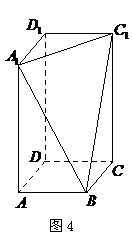 过
过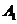 、
、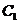 、
、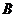 三点的平面截去长方体的一个角后,得到如图4所示的几何体
三点的平面截去长方体的一个角后,得到如图4所示的几何体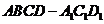 ,且这个几何体的体积为
,且这个几何体的体积为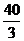 .
.
(1)求棱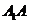 的长;
的长;
(2)在线段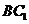 上是否存在点
上是否存在点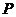 ,使直线
,使直线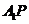 与
与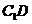 垂直,
垂直,
如果存在,求线段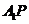 的长,如果不存在,请说明理由.
的长,如果不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com