
5.(2001年春,12)下列四组物质中,两种分子不具有相同核外电子总数的是
A.H2O2和CH3OH B.HNO2和HClO
C.H2O和CH4 D.H2S和F2
4.(2001年春,16)氯的原子序数为17,35Cl是氯的一种同位素,下列说法正确的是
A.35Cl原子所含质子数为18
B.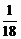 mol的H35Cl分子所含中子数约为6.02×1023
mol的H35Cl分子所含中子数约为6.02×1023
C.3.5 g的35Cl2气体的体积为2.24 L
D.35Cl2气体的摩尔质量为70 g·mol-1
3.(2002年上海,2)C60与现代足球 有很相似的结构,它与石墨互为
A.同位素 B.同素异形体
C.同分异构体 D.同系物
2.(2002年上海综合,44)碳元素有多种同位素,其中14C具有放射性,它能自发放出某种射线,而衰变成其他元素。考古学对出土生物遗骸的年代断定可以使用多种方法,其中较精确的一种是基于14C放射性的方法,但被断定的年代一般不超过5万年。下列考古遗址发现的遗物中能用14C测定年代的是
A.战国曾侯乙墓的青铜编钟(距今约2400年)
B.马家窑文化遗址的粟(距今约5300年)
C.秦始皇兵马俑(距今约2200年)
D.元谋人的门齿(距今约170万年)

1.(2002年上海,11)已知自然界氧的同位素有16O、17O、18O,氢的同位素有H、D,从水分子的原子组成来看,自然界的水一共有
A.3种 B.6种 C.9种 D.12种
5. 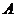 、
、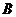 两个代表队进行乒乓球对抗赛,每队三名队员,
两个代表队进行乒乓球对抗赛,每队三名队员,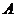 队队员是
队队员是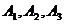 ,
,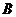 队队员是
队队员是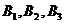 ,按以往多次比赛的统计,对阵队员之间胜负概率如下:
,按以往多次比赛的统计,对阵队员之间胜负概率如下:
|
对阵队员 |
A队队员胜的概率 |
B队队员胜的概率 |
|
A1对B1 |
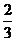 |
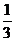 |
|
A2对B2 |
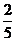 |
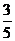 |
|
A3对B3 |
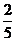 |
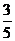 |
现按表中对阵方式出场,每场胜队得1分,负队得0分,设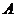 队,
队,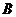 队最后所得分分别为
队最后所得分分别为 ,
,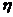

(1)求 ,
,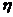 的概率分布; (2)求
的概率分布; (2)求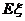 ,
,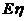
解:(Ⅰ)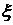 ,
,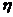 的可能取值分别为3,2,1,0
的可能取值分别为3,2,1,0
根据题意知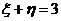 ,所以
,所以
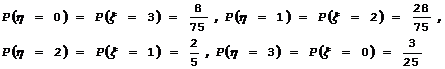
(Ⅱ)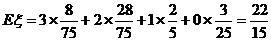 ;
;
因为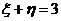 ,所以
,所以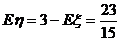

4.一个袋子里装有大小相同的3个红球和2个黄球,从中同时取出2个,含红球个数的数学期望是 1.2 
解:从5个球中同时取出2个球,出现红球的分布列为
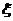 |
0 |
1 |
2 |
|
P |
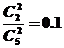 |
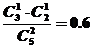 |
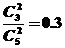 |
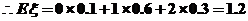
3.学校新进了三台投影仪用于多媒体教学,为保证设备正常工作,事先进行独立试验,已知各设备产生故障的概率分别为p1、p2、p3,求试验中三台投影仪产生故障的数学期望
解:设 表示产生故障的仪器数,Ai表示第i台仪器出现故障(i=1、2、3)
表示产生故障的仪器数,Ai表示第i台仪器出现故障(i=1、2、3)
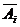 表示第i台仪器不出现故障,则:
表示第i台仪器不出现故障,则:
p( =1)=p(A1·
=1)=p(A1·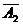 ·
·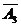 )+ p(
)+ p(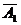 ·A2·
·A2·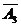 )+ p(
)+ p(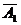 ·
·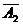 ·A3)
·A3)
=p1(1-p2) (1-p3)+ p2(1-p1) (1-p3)+ p3(1-p1) (1-p2)
= p1+ p2+p3-2p1p2-2p2p3-2p3p1+3p1p2p3
p( =2)=p(A1· A2·
=2)=p(A1· A2·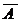 )+ p(A1·
)+ p(A1·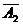 ·
·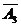 )+ p(
)+ p(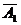 ·A2·A3)
·A2·A3)
= p1p2 (1-p3)+ p1p3(1-p2)+ p2p3(1-p1)
= p1p2+ p1p3+ p2p3-3p1p2p3
p( =3)=p(A1· A2·A3)= p1p2p3
=3)=p(A1· A2·A3)= p1p2p3
∴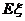 =1×p(
=1×p( =1)+2×p(
=1)+2×p( =2)+3×p(
=2)+3×p( =3)= p1+p2+p3
=3)= p1+p2+p3 
注:要充分运用分类讨论的思想,分别求出三台仪器中有一、二、三台发生故障的概率后再求期望
2.袋中有4个黑球、3个白球、2个红球,从中任取2个球,每取到一个黑球记0分,每取到一个白球记1分,每取到一个红球记2分,用 表示得分数
表示得分数
①求 的概率分布列
的概率分布列
②求 的数学期望
的数学期望
解:①依题意 的取值为0、1、2、3、4
的取值为0、1、2、3、4
 =0时,取2黑
p(
=0时,取2黑
p( =0)=
=0)=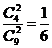
 =1时,取1黑1白 p(
=1时,取1黑1白 p( =1)=
=1)=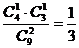
 =2时,取2白或1红1黑p(
=2时,取2白或1红1黑p( =2)=
=2)= 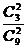 +
+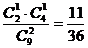
 =3时,取1白1红,概率p(
=3时,取1白1红,概率p( =3)=
=3)= 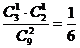
 =4时,取2红,概率p(
=4时,取2红,概率p( =4)=
=4)= 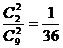
 |
0 |
1 |
2 |
3 |
4 |
|
p |
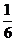 |
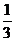 |
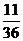 |
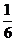 |
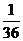 |
∴ 分布列为
分布列为
(2)期望E =0×
=0×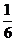 +1×
+1×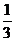 +2×
+2×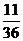 +3×
+3×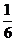 +4×
+4×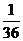 =
=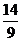
1.一袋子里装有大小相同的3个红球和两个黄球,从中同时取出2个,则其中含红球个数的数学期望是 (用数字作答)
解:令取取黄球个数 (=0、1、2)则
(=0、1、2)则 的要布列为
的要布列为
 |
0 |
1 |
2 |
|
p |
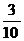 |
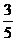 |
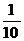 |
于是 E( )=0×
)=0×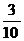 +1×
+1×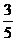 +2×
+2×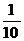 =0.8
=0.8
故知红球个数的数学期望为1.2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com