
8. 离散型随机变量的几何分布:在独立重复试验中,某事件第一次发生时,所作试验的次数ξ也是一个正整数的离散型随机变量.“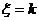 ”表示在第k次独立重复试验时事件第一次发生.如果把k次试验时事件A发生记为
”表示在第k次独立重复试验时事件第一次发生.如果把k次试验时事件A发生记为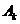 、事件A不发生记为
、事件A不发生记为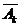 ,P(
,P(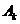 )=p,P(
)=p,P(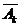 )=q(q=1-p),那么
)=q(q=1-p),那么
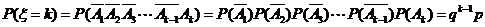 (k=0,1,2,…,
(k=0,1,2,…, 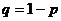 ).于是得到随机变量ξ的概率分布如下:
).于是得到随机变量ξ的概率分布如下:
|
ξ |
1 |
2 |
3 |
… |
k |
… |
|
P |
 |
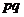 |
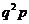 |
… |
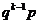 |
… |
称这样的随机变量ξ服从几何分布
记作g(k,p)= 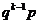 ,其中k=0,1,2,…,
,其中k=0,1,2,…,
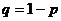 .
.
7.离散型随机变量的二项分布:在一次随机试验中,某事件可能发生也可能不发生,在n次独立重复试验中这个事件发生的次数ξ是一个随机变量.如果在一次试验中某事件发生的概率是P,那么在n次独立重复试验中这个事件恰好发生k次的概率是
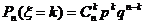 ,(k=0,1,2,…,n,
,(k=0,1,2,…,n,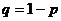 ).
).
于是得到随机变量ξ的概率分布如下:
|
ξ |
0 |
1 |
… |
k |
… |
n |
|
P |
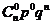 |
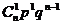 |
… |
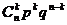 |
… |
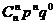 |
称这样的随机变量ξ服从二项分布,记作ξ-B(n,p),其中n,p为参数,并记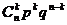 =b(k;n,p).
=b(k;n,p).
6. 分布列的两个性质: ⑴Pi≥0,i=1,2,…; ⑵P1+P2+…=1.
5. 分布列:设离散型随机变量ξ可能取得值为x1,x2,…,x3,…,
ξ取每一个值xi(i=1,2,…)的概率为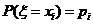 ,则称表
,则称表
|
ξ |
x1 |
x2 |
… |
xi |
… |
|
P |
P1 |
P2 |
… |
Pi |
… |
为随机变量ξ的概率分布,简称ξ的分布列 
4.离散型随机变量与连续型随机变量的区别与联系: 离散型随机变量与连续型随机变量都是用变量表示随机试验的结果;但是离散型随机变量的结果可以按一定次序一一列出,而连续性随机变量的结果不可以一一列出
若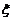 是随机变量,
是随机变量,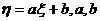 是常数,则
是常数,则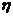 也是随机变量
也是随机变量 并且不改变其属性(离散型、连续型)
并且不改变其属性(离散型、连续型) 
3.连续型随机变量: 对于随机变量可能取的值,可以取某一区间内的一切值,这样的变量就叫做连续型随机变量
2. 离散型随机变量:对于随机变量可能取的值,可以按一定次序一一列出,这样的随机变量叫做离散型随机变量
1.随机变量:如果随机试验的结果可以用一个变量来表示,那么这样的变量叫做随机变量 随机变量常用希腊字母ξ、η等表示
随机变量常用希腊字母ξ、η等表示
12.设A={x|x2-ax+a2-19=0},B={x|x2-5x+6=0},C={x|x2+2x-8=0}.
(1)A∩B=A∪B,求a的值;
(2)∅ 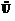 A∩B,且A∩C=∅,求a的值;
A∩B,且A∩C=∅,求a的值;
(3)A∩B=A∩C≠∅,求a的值.
解:(1)因为A∩B=A∪B,所以A=B,又由对应系数相等可得a=5和a2-19=6同时成立,即a=5.
(2)由于B={2,3},C={-4,2},且∅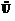 A∩B,A∩C=∅,故只可能3∈A.此时a2-3a-10=0,
A∩B,A∩C=∅,故只可能3∈A.此时a2-3a-10=0,
即a=5或a=-2,
由(1)可知,当a=5时,A=B={2,3},
此时A∩C≠∅,与已知矛盾,所以a=5舍去,故a=-2.
(3)由于B={2,3},C={-4,2},且A∩B=A∩C≠∅,
此时只可能2∈A,即a2-2a-15=0,
也即a=5或a=-3,
由(2)可知a=5不合题意,故a=-3.
11.(文)(2009·北京高考)设A是整数集的一个非空子集.对于k∈A,如果k-1∉A,且k+
1∉A,那么称k是A的一个“孤立元”.给定S={1,2,3,4,5,6,7,8},由S的3个元素构成的所有集合中,不含“孤立元”的集合共有 个.
解析:依题可知,由S的3个元素构成的所有集合中,不含“孤立元”,这三个元素一定是相连的三个数.故这样的集合共有6个.
答案:6
(理)对任意两个集合M、N,定义:M-N={x|x∈M且x∉N},M*N=(M-N)∪(N-M),设M={y|y=x2,x∈R},N={y|y=3sinx,x∈R},则M*N= .
解析:依题意有M=,
所以M-N=(3,+∞),N-M=[-3,0),
故M*N=(M-N)∪(N-M)=[-3,0)∪(3,+∞).
答案:[-3,0)∪(3,+∞)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com