
3.(辽宁)
(22)(本小题满分10分)选修4-1:几何证明讲 

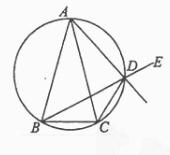 已知
已知
 ABC 中,AB=AC, D是
ABC 中,AB=AC, D是  ABC外接圆劣弧
ABC外接圆劣弧 上的点(不与点A,C重合),延长BD至E。
上的点(不与点A,C重合),延长BD至E。
(1)求证:AD的延长线平分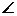 CDE;
CDE;
(2)若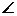 BAC=30,
BAC=30,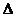 ABC中BC边上的高为2+
ABC中BC边上的高为2+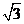 ,求
,求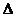 ABC外接圆的面积。
ABC外接圆的面积。 

(23)(本小题满分10分)选修4-4 :坐标系与参数方程在直角坐标系xOy中,以O为极点,x正半轴为极轴建立极坐标系,曲线C的极坐标方程为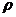 cos(
cos(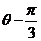 )=1,M,N分别为C与x轴,y轴的交点。
)=1,M,N分别为C与x轴,y轴的交点。
(1)写出C的直角坐标方程,并求M,N的极坐标; 

(2)设MN的中点为P,求直线OP的极坐标方程。
(24)(本小题满分10分)选修4-5:不等式选讲
设函数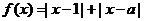 。
。
(1)若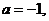 解不等式
解不等式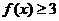 ;
;
(2)如果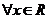 ,
,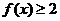 ,求
,求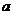 的取值范围。
的取值范围。 

15.(几何证明选讲选做题)如图4,点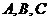 是圆
是圆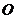 上的点, 且
上的点, 且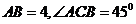 ,则圆
,则圆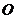 的面积等于 .
的面积等于 .
14. (不等式选讲选做题)不等式
(不等式选讲选做题)不等式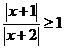 的实数解为 .
的实数解为 .
13.(坐标系与参数方程选做题)若直线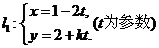 与直线
与直线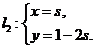 (
(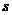 为参数)垂直,则
为参数)垂直,则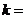 .
.
2.(广东)
1.(福建21)(1)(本小题满分7分)选修4-4:矩阵与变换 

已知矩阵M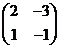 所对应的线性变换把点A(x,y)变成点A ‘(13,5),试求M的逆矩阵及点A的坐标
所对应的线性变换把点A(x,y)变成点A ‘(13,5),试求M的逆矩阵及点A的坐标
(2)(本小题满分7分)选修4-4:坐标系与参数方程
已知直线l:3x+4y-12=0与圆C: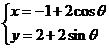 (
(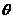 为参数 )试判断他们的公共点个数
为参数 )试判断他们的公共点个数
(3)(本小题满分7分)选修4-5:不等式选讲
解不等式∣2x-1∣<∣x∣+1
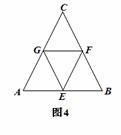
32. 解:(1)图中共有5个三角形;··········································· (2分)
(2)△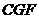 ≌△
≌△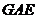 . ·············································· (3分)
. ·············································· (3分)
∵ △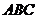 是等边三角形,∴ ∠
是等边三角形,∴ ∠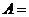 ∠
∠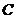 .···················· (4分)
.···················· (4分)
∵ 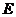 、
、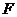 、
、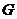 是边
是边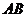 、
、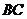 、
、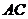 的中点,
的中点,
∴AE=AG=CG=CF=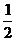 AB. ···································································· (6分)
AB. ···································································· (6分)
∴ △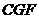 ≌△
≌△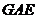 . ········································································· (7分)
. ········································································· (7分)
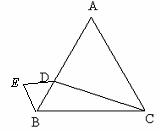
31. (1)如图:
(2)证明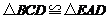 即可.
即可.
30. 解:(1)略.
(2)证明:∵BC=BD,点E是BC的中点,点F是BD的中点,
∴BE=BF.又∠ABC=∠ABD,AB=AB,∴△ABE≌△ABF.
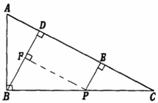
29. 解:(1)如右图;
(2)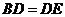 .
.
理由:过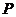 作
作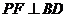 于
于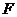 ,四边形
,四边形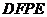 为矩形,
为矩形,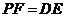 .
.
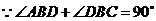 ,
,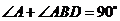 ,
,
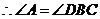 .
.
在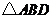 和
和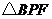 中,
中,
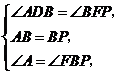
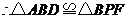 .
.
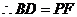 .
.
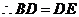 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com