
3.(2008·安徽理,8)若过点A(4,0)的直线l与曲线(x-2)2+y2=1有公共点,则直线l的斜率的取值范围为 ( )
A.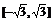 B.
B.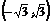
C. 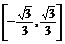 D.
D.
答案 C
2.过点(-1,3)且平行于直线x-2y+3=0的直线方程为 ( )
A.x-2y+7=0 B.2x+y-1=0
C.x-2y-5=0 D.2x+y-5=0
答案 A
1.(2008·福建文,2)“a=1”是“直线x+y=0和直线x-ay=0互相垂直”的 ( )
A.充分而不必要条件 ?B.必要而不充分条件
C.充要条件 ? D.既不充分也不必要条件
答案 C
12.设O为坐标原点,曲线x2+y2+2x-6y+1=0上有两点P、Q,满足关于直线x+my+4=0对称,又满足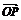 ·
·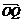 =0.
=0.
(1)求m的值;
(2)求直线PQ的方程.
解 (1)曲线方程为(x+1)2+(y-3)2=9表示圆心为
(-1,3),半径为3的圆.
∵点P、Q在圆上且关于直线x+my+4=0对称,
∴圆心(-1,3)在直线上,代入得m=-1.
(2)∵直线PQ与直线y=x+4垂直,
∴设P(x1,y1)、Q(x2,y2),PQ方程为y=-x+b.
将直线y=-x+b代入圆的方程,
得2x2+2(4-b)x+b2-6b+1=0.
?Δ=4(4-b)2-4×2×(b2-6b+1)>0,
得2-3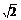 <b<2+3
<b<2+3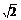 .
.
由根与系数的关系得
x1+x2=-(4-b),x1·x2=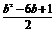 .
.
y1·y2=b2-b(x1+x2)+x1·x2=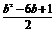 +4b.
+4b.
∵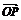 ·
·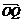 =0,
=0,
∴x1x2+y1y2=0,即b2-6b+1+4b=0,
解得b=1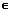 (2-3
(2-3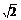 ,2+3
,2+3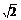 ),
),
∴所求的直线方程为y=-x+1.
章末检测七
11.已知圆C:x2+y2-2x+4y-4=0,问是否存在斜率是1的直线l,使l被圆C截得的弦AB,以AB为直径的圆经过原点,若存在,写出直线l的方程;若不存在,说明理由.
解 假设存在直线l满足题设条件,设l的方程为y=x+m,圆C化为(x-1)2+(y+2)2=9,圆心C(1,-2),则AB中点N是两直线x-y+m=0与y+2=-(x-1)的交点即N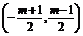 ,以AB为直径的圆经过原点,
,以AB为直径的圆经过原点,
∴|AN|=|ON|,又CN⊥AB,|CN|=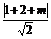 ,
,
∴|AN|=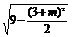 .
.
又|ON|=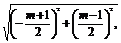
由|AN|=|ON|,解得m=-4或m=1.
∴存在直线l,其方程为y=x-4或y=x+1.
10.已知曲线C:x2+y2-4ax+2ay-20+20a=0.
(1)证明:不论a取何实数,曲线C必过定点;
(2)当a≠2时,证明曲线C是一个圆,且圆心在一条直线上;
(3)若曲线C与x轴相切,求a的值.
(1)证明 曲线C的方程可变形为
(x2+y2-20)+(-4x+2y+20)a=0,
由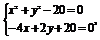 解得
解得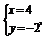
点(4,-2)满足C的方程,故曲线C过定点(4,-2).
(2)证明 原方程配方得(x-2a)2+(y+a)2=5(a-2)2,
∵a≠2时,5(a-2)2>0,
∴C的方程表示圆心是(2a,-a),半径是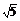 |a-2|的圆.
|a-2|的圆.
设圆心坐标为(x,y),则有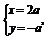
消去a得y=-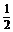 x,故圆心必在直线y=-
x,故圆心必在直线y=-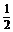 x上.
x上.
(3)解 由题意得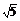 |a-2|=|a|,解得a=
|a-2|=|a|,解得a=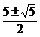
9.已知圆C:x2+y2+2x-4y+3=0.若圆C的切线在x轴和y轴上的截距的绝对值相等,求此切线的方程.
解 ∵切线在两坐标轴上截距的绝对值相等,
∴切线的斜率是±1或过原点.
切线不过原点时,设切线方程为y=-x+b或y=x+c,分别代入圆C的方程得
2x2-2(b-3)x+(b2-4b+3)=0或2x2+2(c-1)x+(c2-4c+3)=0,
由于相切,则方程有等根,∴Δ1=0,
即[2(b-3)]2-4×2×(b2-4b+3)=-b2+2b+3=0,
∴b=3或-1,
?Δ2=0,
即[2(c-1)]2-4×2×(c2-4c+3)=-c2+6c-5=0.
∴c=5或1,
当切线过原点时,设切线为y=kx,即kx-y=0.
由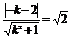 ,得k=2±
,得k=2±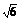 .
.
∴y=(2±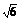 )x,
)x,
故所求切线方程为:
x+y-3=0,x+y+1=0,x-y+5=0,x-y+1=0,y=(2±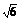 )x.
)x.
8.(2008·湖南文,14)将圆x2+y2=1沿x轴正向平移1个单位后得到圆C,则圆C的方程是 ;若过点(3,0)的直线l和圆C相切,则直线l的斜率是 .
答案 (x-1)2+y2=1 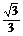 或-
或-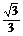
7.设直线ax-y+3=0与圆(x-1)2+(y-2)2=4相交于A、B两点,且弦AB的长为2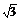 ,则a= .
,则a= .
答案 0
6.(2008·湖北理,9)过点A(11,2)作圆x2+y2+2x-4y-164=0的弦,其中弦长为整数的共有( ) A.16条 B.17条 ? C.32条 ?D.34条
答案?C?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com