
1.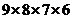 =
=
A. 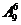 B.
B.
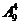 C.
C. 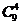 D.
D. 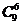
22.(14分)在直角坐标系xOy中,以O为圆心的圆与直线x-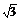 y=4相切.
y=4相切.
(1)求圆O的方程;
(2)圆O与x轴相交于A、B两点,圆内的动点P使|PA|、|PO|、|PB|成等比数列,求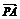 ·
·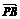 取值范围.
取值范围.
解 (1)依题设,圆O的半径r等于原点O到直线x-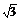 y=4的距离,即r=
y=4的距离,即r= =2.
=2.
所以圆O的方程为x2+y2=4.
(2)不妨设A(x1,0),B(x2,0),且x1<x2,由x2=4,
得A(-2,0),B(2,0).
设P(x,y),由|PA|、|PO|、|PB|成等比数列,
得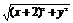 ·
·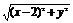 =x2+y2,
=x2+y2,
即x2-y2=2.
所以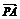 ·
·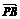 =(-2-x,-y)·(2-x,-y)
=(-2-x,-y)·(2-x,-y)
=x2-4+y2=2(y2-1).
由于点P在圆O内,故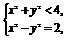
由此得0≤y2<1.
所以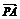 ·
·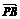 的取值范围为[-2,0).
的取值范围为[-2,0).
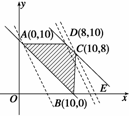
21.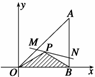 (12分)将一块直角三角板ABO置于平面直角坐标系中(如图所示).已知AB=OB=1,AB⊥OB,点P
(12分)将一块直角三角板ABO置于平面直角坐标系中(如图所示).已知AB=OB=1,AB⊥OB,点P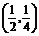 是三角板内一点.现因三角板中阴影部分受到损坏,要把损坏部分锯掉,可用经过点P的任一直线MN将三角板锯成△AMN.问应如何确定直线MN的斜率,可使锯成的△AMN的面积最大?
是三角板内一点.现因三角板中阴影部分受到损坏,要把损坏部分锯掉,可用经过点P的任一直线MN将三角板锯成△AMN.问应如何确定直线MN的斜率,可使锯成的△AMN的面积最大?
解 由题意可知B(1,0),A(1,1),
kOP=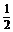 ,kPB=-
,kPB=-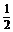 ,
,
∴kMN∈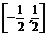 ,lAO:y=x;lAB:x=1.
,lAO:y=x;lAB:x=1.
设lMN:y=kx+b,
∵直线MN过P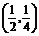
∴b=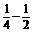 k,∴y=kx+
k,∴y=kx+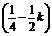 .
.
∴M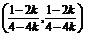 ,N
,N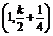
S△AMN=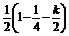 ×
×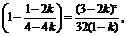
设t=1-k∈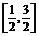 .
.
S△AMN=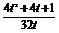 在t∈
在t∈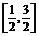 时,函数单调递增.
时,函数单调递增.
∴当t=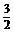 ,即k=-
,即k=-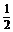 时,S△AMN(max)=
时,S△AMN(max)=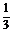 .
.
20.(12分)已知圆M:x2+y2-2mx-2ny+m2-1=0与圆N:x2+y2+2x+2y-2=0交于A、B两点,且这两点平分圆N的圆周,求圆M的圆心的轨迹方程,并求其中半径最小时圆M的方程.
解 由圆M的方程知M(m,n).又由方程组
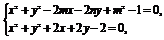 得直线AB的方程为2(m+1)x+2(n+1)y-m2-1=0.
得直线AB的方程为2(m+1)x+2(n+1)y-m2-1=0.
又AB平分圆N的圆周,
所以圆N的圆心N(-1,-1)在直线AB上.
∴2(m+1)(-1)+2(n+1)(-1)-m2-1=0.
∴m2+2m+2n+5=0,即(m+1)2=-2(n+2). (*)
∴(x+1)2=-2(y+2)即为点M的轨迹方程.
又由题意可知当圆M的半径最小时,点M到AB的距离最小,即MN最小.
d=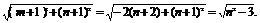
由(*)可知n≤-2,∴d≥1.
即最小值为1,此时m=-1,n=-2,
故此时圆M的方程为(x+1)2+(y+2)2=5.
19.(12分)A、B、C三城市分别有某种机器10台、10台、8台,支援D市18台、E市10台.从A市调一台机器到D、E两市的运费分别为200元和800元;从B市调一台机器到D、E两市的运费分别为300元和700元;从C市调一台机器到D、E两市的运费分别为400元和500元.
(1)若从A、B两市各调x台到D市,当三市28台机器全部调运完毕后,求总运费P(x)关于x的函数表达式,并求P(x)的最大值和最小值;
(2)若从A市调x台到D市,从B市调y台到D市,当28台机器全部调运完毕后,用x、y表示总运费P,并求P的最大值和最小值.
解 (1)机器调运方案如下表:
 方 |
A |
B |
C |
需量 |
|
D |
200x |
300x |
400(18-2x) |
18 |
|
E |
800(10-x) |
700(10-x) |
500(2x-10) |
10 |
|
供量 |
10 |
10 |
8 |
|
总运费P(x)=200x+300x+400(18-2x)+800(10-x)+700(10-x)+500(2x-10)=17 200-800x,
 又由0≤x≤10,0≤18-2x≤8,得定义域5≤x≤9,
又由0≤x≤10,0≤18-2x≤8,得定义域5≤x≤9,
所以P(x)max=P(5)=13 200(元),
P(x)min=P(9)=10 000(元),
(2)机器调运方案如下表:
 方 |
A |
B |
C |
需量 |
|
D |
200x |
300y |
400(18-x-y) |
18 |
|
E |
800(10-x) |
700(10-y) |
500(x+y-10) |
10 |
|
供量 |
10 |
10 |
8 |
|
总运费P=200x+300y+400(18-x-y)+800(10-x)+700(10-y)+500(x+y-10)=17 200-100(5x+3y), 其中0≤x≤10,0≤y≤10,0≤18-x-y≤8.
在xOy平面内作出上述不等式的可行域(如图中阴影部分).其中l1:x+y=18,l2:x+y=10.可见,当x=10,y=8时,Pmin=9 800;当x=0,y=10时,Pmax=14 200.
18.(12分)已知方程x2+y2-2x-4y+m=0.
(1)若此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于M、N两点,且OM⊥ON(O为坐标原点),求m;
(3)在(2)的条件下,求以MN为直径的圆的方程.
解 (1)(x-1)2+(y-2)2=5-m,∴m<5.
(2)设M(x1,y1),N(x2,y2),
则x1=4-2y1,x2=4-2y2,
则x1x2=16-8(y1+y2)+4y1y2
∵OM⊥ON,∴x1x2+y1y2=0
∴16-8(y1+y2)+5y1y2=0 ①
由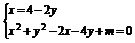
得5y2-16y+m+8=0
∴y1+y2=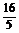 ,y1y2=
,y1y2=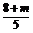 ,代入①得,m=
,代入①得,m=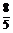 .
.
(3)以MN为直径的圆的方程为
(x-x1)(x-x2)+(y-y1)(y-y2)=0
即x2+y2-(x1+x2)x-(y1+y2)y=0
∴所求圆的方程为x2+y2-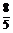 x-
x-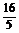 y=0.
y=0.
17.(12分)过点M(0,1)作直线,使它被直线l1:x-3y+10=0和l2:2x+y-8=0所截得的线段恰好被M平分,求此直线方程.
解 方法一 过点M且与x轴垂直的直线是y轴,它和两已知直线的交点分别是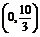 和(0,8),显然不满足中点是点M(0,1)的条件.
和(0,8),显然不满足中点是点M(0,1)的条件.
故可设所求直线方程为y=kx+1,与已知两直线l1,l2分别交于A、B两点,联立方程组
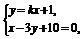 ①
①
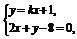 ②
②
由①解得xA=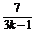 ,由②解得xB=
,由②解得xB=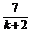 .
.
∵点M平分线段AB,
∴xA+xB=2xM,即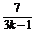 +
+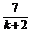 =0.
=0.
解得k=-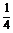 ,故所求直线方程为x+4y-4=0.
,故所求直线方程为x+4y-4=0.
方法二 设所求直线与已知直线l1,l2分别交于A、B两点.
∵点B在直线l2:2x+y-8=0上,
故可设B(t,8-2t),M(0,1)是AB的中点.
由中点坐标公式得A(-t,2t-6).
∵A点在直线l1:x-3y+10=0上,
∴(-t)-3(2t-6)+10=0,解得t=4.
∴B(4,0),A(-4,2),故所求直线方程为x+4y-4=0.
16.(2008·上海扬浦测试)若直线ax+by=1与圆x2+y2=1相切,则实数ab的取值范围是 .
答案 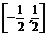
15.已知点P(m,n)位于第一象限,且在直线x+y-1=0上,则使不等式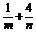 ≥a恒成立的实数a的取值范围是
.
≥a恒成立的实数a的取值范围是
.
答案 (-∞,9]
14.在坐标平面上有两个区域M和N,其中区域M=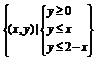 ,区域N={(x,y)|t≤x≤t+1,0≤t≤1},区域M和N公共部分的面积用函数f(t)表示,则f(t)的表达式为
.
,区域N={(x,y)|t≤x≤t+1,0≤t≤1},区域M和N公共部分的面积用函数f(t)表示,则f(t)的表达式为
.
答案 f(t)=-t2+t+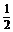
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com