
6.设△ABC的一个顶点是A(3,-1),∠B,∠C的平分线方程分别为x=0,y=x,则直线BC的方程是( )
A.y=2x+5 B.y=2x+3
C.y=3x+5? D.y=-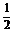 x+
x+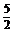
答案?A
5.曲线f(x,y)=0关于直线x-y-2=0对称的曲线方程是 ( )
?A.f(y+2,x)=0 B.f(x-2,y)=0
?C.f(y+2,x-2)=0 D.f(y-2,x+2)=0
答案?C
4.已知三条直线l1:y=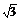 x-1,l2:y=1,l3:x+y+1=0,l1与l2的夹角为
x-1,l2:y=1,l3:x+y+1=0,l1与l2的夹角为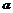 ,l2与l3的夹角为
,l2与l3的夹角为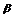 ,则
,则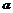 +
+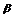 的值为( ) A.75°? ?B.105° C.165° D.195°?
的值为( ) A.75°? ?B.105° C.165° D.195°?
答案?B?
3.已知直线l1的方向向量a=(1,3),直线l2的方向向量b=(-1,k),若直线l2经过点(0,5),且l1⊥l2,则直线l2的方程为 ( )
A.x+3y-5=0 B.x+3y-15=0
C.x-3y+5=0 D.x-3y+15=0
答案 B
2.A、B是x轴上两点,点P的横坐标为2,且|PA|=|PB|,若直线PA的方程为x-y+1=0,则直线PB的方程为 ( )
A.2x-y-1=0 B.x+y-5=0
C.2x+y-7=0 D.2y-x-4=0
答案 B
1.(2008·全国Ⅱ文)原点到直线x+2y-5=0的距离为 ( )
A.1 B.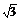 C.2 D.
C.2 D.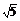
答案 D
4.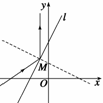 光线沿直线l1:x-2y+5=0射入,遇直线l:3x-2y+7=0后反射,求反射光线所在的直线方程.
光线沿直线l1:x-2y+5=0射入,遇直线l:3x-2y+7=0后反射,求反射光线所在的直线方程.
解 方法一 由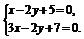
得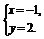
∴反射点M的坐标为(-1,2).
又取直线x-2y+5=0上一点P(-5,0),设P关于直线l的对称点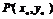 ,由P
,由P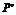 ⊥l可知,
⊥l可知,
kPP′=-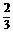 =
=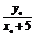 .
.
而PP′的中点Q的坐标为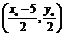 ,
,
Q点在l上,∴3·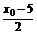 -2·
-2·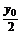 +7=0.
+7=0.
由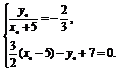 得
得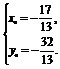
根据直线的两点式方程可得l的方程为
29x-2y+33=0.
方法二 设直线x-2y+5=0上任意一点P(x0,y0)关于直线l的对称点为P′(x,y),
则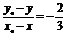 ,
,
又PP′的中点Q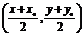 在l上,
在l上,
∴3×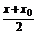 -2×
-2×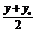 +7=0,
+7=0,
由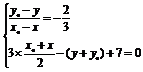
可得P点的坐标为
x0=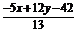 ,y0=
,y0=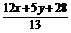 ,
,
代入方程x-2y+5=0中,
化简得29x-2y+33=0,
即为所求反射光线所在的直线方程.

3.已知三条直线l1:2x-y+a=0(a>0),直线l2:4x-2y-1=0和直线l3:x+y-1=0,且l1与l2的距离是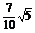 .
.
(1)求a的值;
(2)能否找到一点P,使得P点同时满足下列三个条件:
①P是第一象限的点;②P点到l1的距离是P点到l2的距离的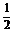 ;③P点到l1的距离与P点到l3的距离之比是
;③P点到l1的距离与P点到l3的距离之比是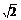 ∶
∶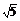 .若能,求P点坐标;若不能,说明理由.
.若能,求P点坐标;若不能,说明理由.
解 (1)l2即为2x-y-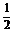 =0,
=0,
∴l1与l2的距离d=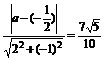 ,
,
∴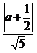 =
=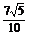 ,∴
,∴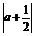 =
=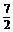 ,
,
∵a>0,∴a=3.
(2)假设存在这样的P点.
设点P(x0,y0),若P点满足条件②,则P点在与l1、l2平行的直线l′:2x-y+C=0上,
且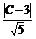 =
=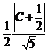 ,即C=
,即C=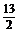 或C=
或C=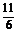 ,
,
∴2x0-y0+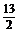 =0或2x0-y0+
=0或2x0-y0+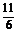 =0;
=0;
若P点满足条件③,由点到直线的距离公式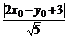 =
=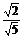 ×
×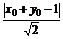 ,
,
即|2x0-y0+3|=|x0+y0-1|,
∴x0-2y0+4=0或3x0+2=0;
由于P点在第一象限,∴3x0+2=0不满足题意.
联立方程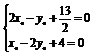 ,
,
解得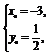 (舍去).
(舍去).
由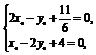 解得
解得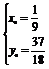
∴假设成立,点P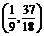 即为同时满足三个条件的点.
即为同时满足三个条件的点.
2.某人在一山坡P处观看对面山顶上的一座铁塔,如图所示,塔高BC=80(米),塔所在的山高OB=220(米),OA=200(米),图中所示的山坡可视为直线l,且点P在直线l上,l与水平地面的夹角为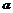 ,tan
,tan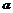 =
=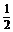 .试问,此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)?
.试问,此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)?
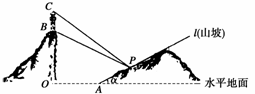
解 如图所示,建立平面直角坐标系,
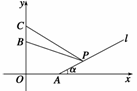
则A(200,0),B(0,220),C(0,300).
直线l的方程为y=(x-200)tan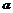 ,则y=
,则y=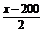 .
.
设点P的坐标为(x,y),则P(x, 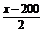 )(x>200).
)(x>200).
由经过两点的直线的斜率公式
kPC=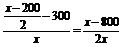 ,
,
kPB=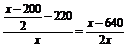 .
.
由直线PC到直线PB的角的公式得
?tan∠BPC=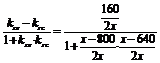
=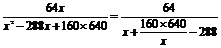 (x>200).
(x>200).
要使tan∠BPC达到最大,只需x+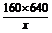 -288达到最小,由均值不等式
-288达到最小,由均值不等式
x+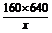 -288≥2
-288≥2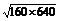 -288,
-288,
当且仅当x=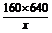 时上式取得等号.
时上式取得等号.
故当x=320时,tan∠BPC最大.
这时,点P的纵坐标y为y=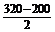 =60.
=60.
由此实际问题知0<∠BPC<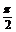 ,所以tan∠BPC最大时,∠BPC最大.故当此人距水平地面60米高时,观看铁塔的视角∠BPC最大.
,所以tan∠BPC最大时,∠BPC最大.故当此人距水平地面60米高时,观看铁塔的视角∠BPC最大.
1.已知两条直线l1:(3+m)x+4y=5-3m,l2:2x+(5+m)y=8.当m分别为何值时,l1与l2:
(1)相交?(2)平行?(3)垂直?
解 当m=-5时,显然,l1与l2相交;
当m≠-5时,易得两直线l1和l2的斜率分别为
k1=-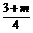 ,k2=-
,k2=-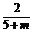 ,
,
它们在y轴上的截距分别为b1=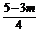 ,b2=
,b2=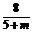 .
.
(1)由k1≠k2,得-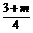 ≠-
≠-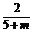 ,
,
m≠-7且m≠-1.
∴当m≠-7且m≠-1时,l1与l2相交.
(2)由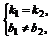 ,得
,得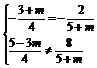 ,m=-7.
,m=-7.
∴当m=-7时,l1与l2平行.
(3)由k1k2=-1,
得-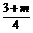 ·
·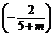 =-1,m=-
=-1,m=-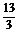 .
.
∴当m=-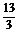 时,l1与l2垂直.
时,l1与l2垂直.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com