
12.(安徽17)某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A到过疫区,B肯定是受A感染的。对于C,因为难以判定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是1/2.同样也假设D受A、B和C感染的概率都是1/3.在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量。写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望)。
11.(浙江19)在1,2,3…,9,这9个自然数中,任取3个数.
(Ⅰ)求这3个数中,恰有一个是偶数的概率; 

(Ⅱ)记ξ为这三个数中两数相邻的组数,(例如:若取出的数1、2、3,则有两组相邻的数1、2和2、3,此时ξ的值是2)。求随机变量ξ的分布列及其数学期望Eξ.
10.(江苏5)现有5根竹竿,它们的长度(单位:m)分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m的概率为 .
9.(福建16)从集合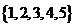 的所有非空子集中,等可能地取出一个。
的所有非空子集中,等可能地取出一个。
(1)记性质r:集合中的所有元素之和为10,求所取出的非空子集满足性质r的概率;
(2)记所取出的非空子集的元素个数为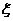 ,求
,求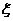 的分布列和数学期望E
的分布列和数学期望E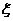 w.w.w.k
w.w.w.k
8.(湖北16)一个盒子里装有4张大小形状完全相同的卡片,分别标有数2,3,4,5;另一个盒子也装有4张大小形状完全相同的卡片,分别标有数3,4,5,6。现从一个盒子中任取一张卡片,其上面的数记为x;再从另一盒子里任取一张卡片,其上面的数记为y,记随机变量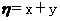 ,求
,求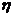 的分布列和数学期望。
的分布列和数学期望。
7.(湖北3)投掷两颗骰子,得到其向上的点数分别为m和n,则复数(m+ni)(n-mi)为实数的概率为
A、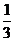 B、
B、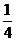 C、
C、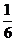 D、
D、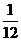
6.(北京17)某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是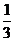 ,遇到红灯时停留的时间都是2min。
,遇到红灯时停留的时间都是2min。
(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率; 

(Ⅱ)求这名学生在上学路上因遇到红灯停留的总时间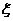 的分布列及期望。
的分布列及期望。
5.(山东19)在某学校组织的一次蓝球定点投蓝训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投三次。某同学在A处的命中率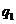 为0.25,在B处的命中率为
为0.25,在B处的命中率为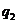 .该同学选择先在A处投一球,以后都在B处投,用
.该同学选择先在A处投一球,以后都在B处投,用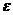 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为

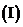 求
求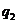 的值;
的值;
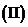 求随机变量
求随机变量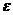 的数学期量
的数学期量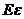 ;
; 

 试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
4.(山东14)若函数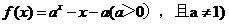 有两个零点,则实数
有两个零点,则实数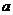 的
的
取值范围是
3.(山东11)在区间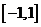 上随机取一个数
上随机取一个数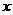 ,
,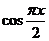 的值介于0到
的值介于0到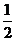 之间的概率为
之间的概率为
(A)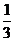 (B)
(B)  (C)
(C) 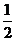 (D)
(D) 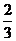 w.w.w.k.s
w.w.w.k.s
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com