
例1.设随机变量ξ的分布列为
|
ξ |
1 |
2 |
… |
n |
|
P |
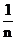 |
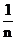 |
… |
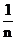 |
求Dξ
解:(略)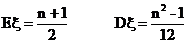

例2.已知离散型随机变量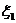 的概率分布为
的概率分布为
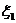 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
P |
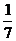 |
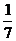 |
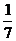 |
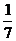 |
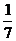 |
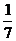 |
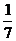 |
离散型随机变量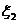 的概率分布为
的概率分布为
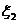 |
3.7 |
3.8 |
3.9 |
4 |
4.1 |
4.2 |
4.3 |
|
P |
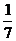 |
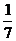 |
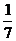 |
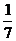 |
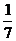 |
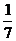 |
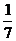 |
求这两个随机变量期望、均方差与标准差
解: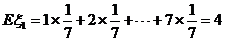 ;
;
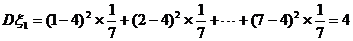 ;
;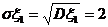

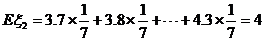 ;
;
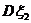 =0.04,
=0.04, 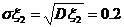 .
.
点评:本题中的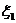 和
和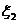 都以相等的概率取各个不同的值,但
都以相等的概率取各个不同的值,但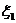 的取值较为分散,
的取值较为分散,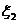 的取值较为集中.
的取值较为集中.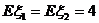 ,
,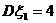 ,
,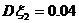 ,方差比较清楚地指出了
,方差比较清楚地指出了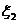 比
比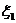 取值更集中.
取值更集中.
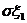 =2,
=2,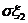 =0.02,可以看出这两个随机变量取值与其期望值的偏差
=0.02,可以看出这两个随机变量取值与其期望值的偏差 
例3.
甲、乙两射手在同一条件下进行射击,分布列如下:射手甲击中环数8,9,10的概率分别为0.2,0.6,0.2;射手乙击中环数8,9,10的概率分别为0.4,0.2,0.24 用击中环数的期望与方差比较两名射手的射击水平
用击中环数的期望与方差比较两名射手的射击水平
解: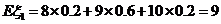
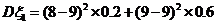 +(10-9)
+(10-9)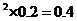 ;
;
同理有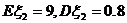

由上可知,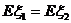 ,
,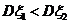
 所以,在射击之前,可以预测甲、乙两名射手所得的平均环数很接近,均在9环左右,但甲所得环数较集中,以9环居多,而乙得环数较分散,得8、10环地次数多些.
所以,在射击之前,可以预测甲、乙两名射手所得的平均环数很接近,均在9环左右,但甲所得环数较集中,以9环居多,而乙得环数较分散,得8、10环地次数多些.
点评:本题中,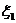 和
和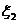 所有可能取的值是一致的,只是概率的分布情况不同.
所有可能取的值是一致的,只是概率的分布情况不同.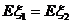 =9,这时就通过
=9,这时就通过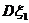 =0.4和
=0.4和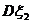 =0.8来比较
=0.8来比较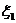 和
和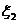 的离散程度,即两名射手成绩的稳定情况
的离散程度,即两名射手成绩的稳定情况 
例4.A、B两台机床同时加工零件,每生产一批数量较大的产品时,出次品的概率如下表所示:
A机床 B机床
|
次品数ξ1 |
0 |
1 |
2 |
3 |
|
次品数ξ1 |
0 |
1 |
2 |
3 |
|
概率P |
0.7 |
0.2 |
0.06 |
0.04 |
|
概率P |
0.8 |
0.06 |
0.04 |
0.10 |
问哪一台机床加工质量较好
解: Eξ1=0×0.7+1×0.2+2×0.06+3×0.04=0.44,
Eξ2=0×0.8+1×0.06+2×0.04+3×0.10=0.44.
它们的期望相同,再比较它们的方差
Dξ1=(0-0.44)2×0.7+(1-0.44)2×0.2+(2-0.44)2
×0.06+(3-0.44)2×0.04=0.6064,
Dξ2=(0-0.44)2×0.8+(1-0.44)2×0.06+(2-0.44)2
×0.04+(3-0.44)2×0.10=0.9264.
∴Dξ1< Dξ2 故A机床加工较稳定、质量较好.
4.其它:
⑴随机变量ξ的方差的定义与一组数据的方差的定义式是相同的;
⑵随机变量ξ的方差、标准差也是随机变量ξ的特征数,它们都反映了随机变量取值的稳定与波动、集中与离散的程度;
⑶标准差与随机变量本身有相同的单位,所以在实际问题中应用更广泛
3.方差的性质:(1)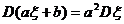 ;(2)
;(2)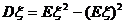 ;
;
(3)若ξ-B(n,p),则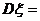 np(1-p)
np(1-p) 
2. 标准差: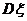 的算术平方根
的算术平方根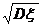 叫做随机变量ξ的标准差,记作
叫做随机变量ξ的标准差,记作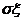 .
.
1. 方差: 对于离散型随机变量ξ,如果它所有可能取的值是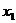 ,
,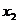 ,…,
,…,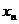 ,…,且取这些值的概率分别是
,…,且取这些值的概率分别是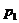 ,
,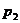 ,…,
,…,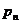 ,…,那么,
,…,那么,
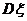 =
=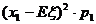 +
+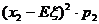 +…+
+…+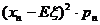 +…
+…
称为随机变量ξ的均方差,简称为方差,式中的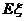 是随机变量ξ的期望.
是随机变量ξ的期望.
13.若ξ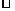 B(n,p),则Eξ=np
B(n,p),则Eξ=np 
12. 期望的一个性质: 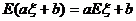
10. 数学期望是离散型随机变量的一个特征数,它反映了离散型随机变量取值的平均水平 
11 平均数、均值:在有限取值离散型随机变量ξ的概率分布中,令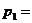
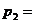 …
…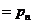 ,则有
,则有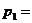
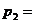 …
…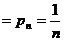 ,
,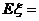
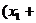
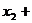 …
…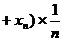 ,所以ξ的数学期望又称为平均数、均值
,所以ξ的数学期望又称为平均数、均值

9.数学期望: 一般地,若离散型随机变量ξ的概率分布为
|
ξ |
x1 |
x2 |
… |
xn |
… |
|
P |
p1 |
p2 |
… |
pn |
… |
则称 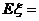
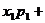
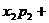 …
…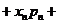 … 为ξ的数学期望,简称期望.
… 为ξ的数学期望,简称期望.
8.几何分布: g(k,p)= 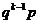 ,其中k=0,1,2,…,
,其中k=0,1,2,…,
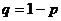 .
.
|
ξ |
1 |
2 |
3 |
… |
k |
… |
|
P |
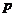 |
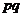 |
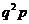 |
… |
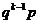 |
… |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com