
19.(江苏16)(本小题满分14分)
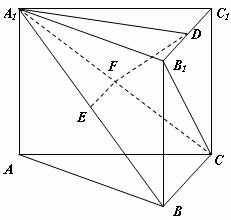 如图,在直三棱柱
如图,在直三棱柱 中,
中, 、
、 分别是
分别是 、
、 的中点,点
的中点,点 在
在 上,
上, 。
。
求证:(1)EF∥平面ABC;
(2)平面
 平面
平面 .
.
 [解析] 本小题主要考查直线与平面、平面与平面得位置关系,考查空间想象能力、推理论证能力。满分14分。
[解析] 本小题主要考查直线与平面、平面与平面得位置关系,考查空间想象能力、推理论证能力。满分14分。

19.(Ⅰ)证明:连接 , 在
, 在 中,
中, 分别是
分别是 的中点,所以
的中点,所以 , 又
, 又 ,所以
,所以 ,又
,又 平面ACD ,DC
平面ACD ,DC 平面ACD, 所以
平面ACD, 所以 平面ACD
平面ACD
(Ⅱ)在 中,
中, ,所以
,所以
而DC 平面ABC,
平面ABC, ,所以
,所以 平面ABC
平面ABC
而 平面ABE, 所以平面ABE
平面ABE, 所以平面ABE 平面ABC, 所以
平面ABC, 所以 平面ABE
平面ABE
由(Ⅰ)知四边形DCQP是平行四边形,所以
所以 平面ABE, 所以直线AD在平面ABE内的射影是AP,
平面ABE, 所以直线AD在平面ABE内的射影是AP,
所以直线AD与平面ABE所成角是
在 中,
中, ,
,
所以
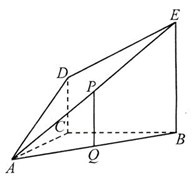
18.(浙江19
|
|
 平面
平面 ,
, ,
, ,
, ,
, 分别为
分别为 的中点.(I)证明:
的中点.(I)证明: 平面
平面 ;(II)求
;(II)求 与平面
与平面 所成角的正弦值.
所成角的正弦值.17.(山东18)((本小题满分12分)
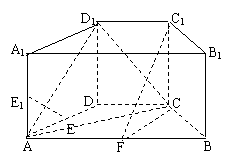
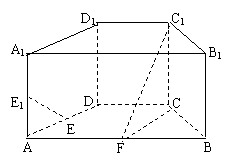 如图,在直四棱柱ABCD-A
如图,在直四棱柱ABCD-A B
B C
C D
D 中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA
中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA =2, E、E
=2, E、E 分别是棱AD、AA
分别是棱AD、AA 的中点.
的中点. 

(1) 设F是棱AB的中点,证明:直线EE //平面FCC
//平面FCC ;
;
(2) 证明:平面D1AC⊥平面BB1C1C.
证明:(1)在直四棱柱ABCD-A B
B C
C D
D 中,取A1B1的中点F1,
中,取A1B1的中点F1,
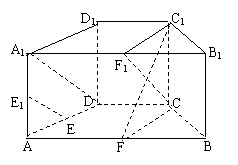 连接A1D,C1F1,CF1,因为AB=4, CD=2,且AB//CD,
连接A1D,C1F1,CF1,因为AB=4, CD=2,且AB//CD,
所以CDA1F1,A1F1CD为平行四边形,所以CF1//A1D,
又因为E、E 分别是棱AD、AA
分别是棱AD、AA 的中点,所以EE1//A1D,
的中点,所以EE1//A1D,
所以CF1//EE1,又因为 平面FCC
平面FCC ,
, 平面FCC
平面FCC ,
,
所以直线EE //平面FCC
//平面FCC .
.
 (2)连接AC,在直棱柱中,CC1⊥平面ABCD,AC
(2)连接AC,在直棱柱中,CC1⊥平面ABCD,AC 平面ABCD,
平面ABCD,
所以CC1⊥AC,因为底面ABCD为等腰梯形,AB=4, BC=2,
F是棱AB的中点,所以CF=CB=BF,△BCF为正三角形,
 ,△ACF为等腰三角形,且
,△ACF为等腰三角形,且
所以AC⊥BC, 又因为BC与CC1都在平面BB1C1C内且交于点C,
所以AC⊥平面BB1C1C,而 平面D1AC,
平面D1AC,
所以平面D1AC⊥平面BB1C1C.
[命题立意]: 本题主要考查直棱柱的概念、线面平行和线面垂直位置关系的判定.熟练掌握平行和垂直的判定定理.完成线线、线面位置关系的转化.
16. (宁夏海南19) (18)(本小题满分12分)
如图,在三棱锥 中,⊿
中,⊿ 是等边三角形,∠PAC=∠PBC=90 º
是等边三角形,∠PAC=∠PBC=90 º
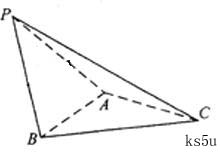 (Ⅰ)证明:AB⊥PC
(Ⅰ)证明:AB⊥PC
(Ⅱ)若 ,且平面
,且平面 ⊥平面
⊥平面 ,
,
求三棱锥 体积。
(18)解:
体积。
(18)解:
(Ⅰ)因为 是等边三角形,
是等边三角形, ,
,
所以 ,可得
,可得 。
。
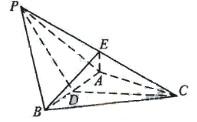
如图,取 中点
中点 ,连结
,连结 ,
, ,
,
 则
则 ,
, ,
,
所以 平面
平面 ,
,
所以 。
......6分
。
......6分 

(Ⅱ)作 ,垂足为
,垂足为 ,连结
,连结 .
.
因为
 ,
,
所以 ,
, .
.
由已知,平面
 平面
平面 ,故
,故 . ......8分
. ......8分
因为 ,所以
,所以 都是等腰直角三角形。
都是等腰直角三角形。
由已知 ,得
,得 ,
,  的面积
的面积 .
.
因为
 平面
平面 ,
,
所以三角锥 的体积
的体积
 .......12分
.......12分
15. (辽宁19)(本小题满分12分)
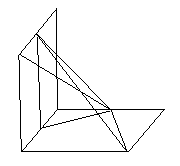
如图,已知两个正方形ABCD 和DCEF不在同一平面内,M,N分别为AB,DF的中点。
(I)若CD=2,平面ABCD ⊥平面DCEF,求直线MN的长;
(II)用反证法证明:直线ME 与 BN 是两条异面直线。 

 (19)解
(19)解
(Ⅰ)取CD的中点G连结MG,NG.
因为ABCD,DCEF为正方形,且边长为2,
所以MG⊥CD,MG=2, .
.
因为平面ABCD⊥平面DCEF,
所以MG⊥平面DCEF,可得MG⊥NG.
所以 ……6分
……6分
(Ⅱ)假设直线ME与BN共面, …..8分
则 平面MBEN,且平面MBEN与平面DCEF交于EN,
平面MBEN,且平面MBEN与平面DCEF交于EN,
由已知,两正方形不共面,故 平面DCEF.
平面DCEF.
又AB∥CD,所以AB∥平面DCEF.而EN为平面MBEN与平面DCEF的交线,
所以AB∥EN.
又AB∥CD∥EF,
所以EN∥EF,这与 矛盾,故假设不成立。
矛盾,故假设不成立。 

所以ME与BN不共面,它们是异面直线。 ……..12分
14. (广东18)(17.(本小题满分13分)
某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P-EFGH,下半部分是长方体ABCD-EFGH.图5、图6分别是该标识墩的正(主)视图和俯视图.
(1)请画出该安全标识墩的侧(左)视图;
(2)求该安全标识墩的体积
(3)证明:直线BD 平面PEG
平面PEG
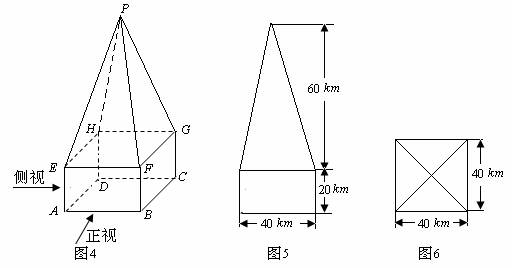
[解析](1)侧视图同正视图,如下图所示.
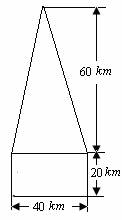
(2)该安全标识墩的体积为:


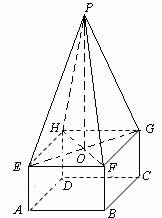
(3)如图,连结EG,HF及 BD,EG与HF相交于O,连结PO.
由正四棱锥的性质可知, 平面EFGH ,
平面EFGH , 
又
 平面PEG
平面PEG
又
 平面PEG;
平面PEG; 

13. (福建20) (本小题满分12分)
如图,平行四边形 中,
中, ,
, 将
将
 沿
沿 折起到
折起到 的位置,使平面
的位置,使平面 平面
平面
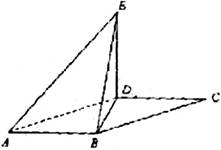 (I)求证:
(I)求证:


(Ⅱ)求三棱锥 的侧面积。
的侧面积。
(I)证明:在 中,
中,

又 平面
平面 平面
平面
平面 平面
平面 平面
平面
 平面
平面
 平面
平面
(Ⅱ)解:由(I)知 从而
从而
在 中,
中,

又 平面
平面 平面
平面

 平面
平面 平面
平面
 ,平面
,平面
而 平面
平面
综上,三棱锥 的侧面积,
的侧面积,
12. (安徽2) 本小题满分13分
如图,ABCD的边长为2的正方形,直线 与平面ABCD平行,E和F式
与平面ABCD平行,E和F式 上的两个不同点,且EA=ED,FB=FC,
上的两个不同点,且EA=ED,FB=FC,  和
和 是平面ABCD内的两点,
是平面ABCD内的两点, 和
和 都与平面ABCD垂直,
都与平面ABCD垂直,
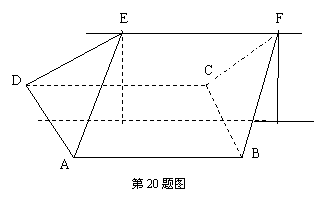 (1)证明:直线
(1)证明:直线 垂直且平分线段AD:
垂直且平分线段AD:
(2)若∠EAD=∠EAB
 ,EF
,EF 2,求多面
2,求多面
体ABCDEF的体积。
解:由 且
且 面ABCD
面ABCD
∴点 在线段AD的垂直平分线上,同理
在线段AD的垂直平分线上,同理
点 在线段BC 的垂直平分线上,又ABCD是正方形
在线段BC 的垂直平分线上,又ABCD是正方形
∴线段BC 的垂直平分线就是线段AD的垂直平分线,即点 、
、 都在线段AD的垂直平分线,所以直线
都在线段AD的垂直平分线,所以直线 垂直且平分线段AD。
垂直且平分线段AD。
(2)连接EB、EC。由题设知,多面体ABCDEF可分割成正四棱锥E-ABCD和正四面体E-BCF两部分。
设AD的中点为M,在Rt△MEE/中,由于ME/=1,ME= ,∴EE/=
,∴EE/=
∴
又
∴多面体ABCDEF的体积为 。
。
11.(辽宁16)设某几何体的三视图如下(尺寸的长度单位为m)。
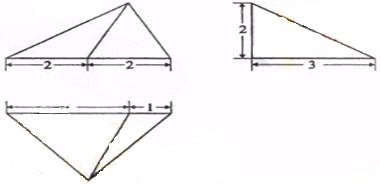
则该几何体的体积为 
[解析]这是一个三棱锥,高为2,底面三角形一边为4,这边上的高为3,
体积等于 ×2×4×3=4
×2×4×3=4
[答案]4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com