
2009年6月13日,温家宝总理在湖南考察时指出,当前经济运行总体形势企稳向好,但是我们一点也不能忽视问题。由于国际金融危机发展的前景还不明朗,不确定的因素还很多,还要准备更长的时间,走曲折的道路。据此回答8-9题。
8.当前经济运行总体形势企稳向好,但是我们一点也不能忽视问题。这一判断和要求坚持了
( )
①从实际出发,实事求是的原则 ②具体问题具体分析的原则
③两点论与重点论的统一 ④事物发展前进性与曲折性的统一
A.①②③ B.①②④
C.①③④ D.②③④
[解析] 上述关于当前经济形势的判断和要求,与具体问题具体分析无关。
[答案] C
9.我们还要准备更长的时间,走曲折的道路。从哲学的角度看,这是因为
( )
A.量的积累达到一定程度才能引起质变
B.曲折的道路对我国的发展更加有利
C.任何事物的发展都不可能一帆风顺
D.人民群众对新事物的认识、理解和接受需要一个过程
[解析] A与材料无关。B的说法错误。当前我们面临的困难并不是人民群众不认识和不支持造成的,故D不符合实际。
[答案] C
7.(2010年汉口模拟)2009年3月20日,我国汽车产业调整和振兴规划正式发布。根据规划,我国将实施新能源汽车战略,启动国家节能和新能源汽车示范工程,由中央财政安排资金给予补贴,支持大中城市示范推广混合动力汽车、纯电动汽车、燃料电池汽车等节能和新能源汽车。国家支持节能和新能源汽车的发展,从哲学的角度看,这是因为
( )
A.这有利于应对金融危机对我国汽车产业的冲击
B.新出现的事物就是新事物
C.它代表了事物的发展方向,符合事物发展规律
D.节能和新能源汽车是高科技产品,附加值高
[解析] A、D不是从哲学的角度看。新出现的事物不一定是新事物,B不选。
[答案] C
“假如生活欺骗了你,不要悲伤,不要心急!忧郁的日子里需要镇静,相信吧,快乐的日子将会来临。”据此回答5-6题。
5.面对生活中遇到的挫折,我们需要
( )
①有坚强的意志和毅力,迎接挑战 ②有战胜挫折的良好心理品质 ③以乐观的心态多走弯路,不惧挫折 ④坚信前途是光明的,要对生活充满信心
A.①②③ B.②③④
C.①③④ D.①②④
[解析] ③错在多走弯路。
[答案] D
6.挫折既是人生路上的“绊脚石”,又是前进路上的“垫脚石”。这种看法
( )
A.坚持了全面的观点看问题
B.正确认识了人的能动作用
C.说明意识能反作用于物质
D.说明量变会最终引起质变
[解析] 既是“绊脚石”又是“垫脚石”,体现了一分为二的观点。
[答案] A
(2010年泰州模拟)李白在《行路难》中写到:“行路难!行路难!多歧路,今安在?长风破浪会有时,直挂云帆济沧海。”据此回答3-4题。
3.“长风破浪会有时,直挂云帆济沧海”的哲学依据是
( )
A.事物的发展是一个由不完善到完善的过程
B.事物的发展是一个由量变到质变的过程
C.事物的发展是前进性和曲折性的统一
D.事物的发展是内外因共同作用的结果
[解析] 这句诗表达的是,我们面对困难,要充满信心,故应选C。
[答案] C
4.从辩证法的角度看,上述材料告诉我们
( )
A.矛盾具有普遍性,事事有矛盾,时时有矛盾
B.在人生的道路上我们会遇到不可克服的困难
C.面对困难我们要充满信心,相信前途是光明的
D.只要我们有信心,就一定能克服一切困难
[解析] 材料强调的是我们面对困难应有的态度,故应选C。
[答案] C
由于网络游戏具有一定的特殊性,未成年人容易沉溺其中,网络游戏产业近十年的发展几经波折。2009年3月,针对未成年网游群体的网络游戏防沉迷系统被强制嵌入运行,作为中国文化创意产业之一的网络游戏产业,正日益步入良性发展轨道。据此回答1-2题。
1. 上述材料体现的辩证法道理是
( )
A.事物发展的总趋势是曲折的
B.事物发展的道路是前进的
C.要学会正确对待人生道路上的曲折
D.任何事物都是在曲折中向前进
[解析] A、B说法错误。C与题干主旨不符。
[答案] D
2.针对未成年网游群体的网络游戏防沉迷系统被强制嵌入运行,这体现的哲理是
( )
A.国家加强对青少年身心健康的保护
B.事物都是一分为二的,要全面地看问题
C.矛盾具有特殊性,要具体问题具体分析
D.事物发展的根据是事物的内部矛盾
[解析] A不是哲理。题干强调的是针对青少年这一群体而采取的措施,体现了具体问题具体分析的原则。B、D与题干主旨不符。
[答案] C
22、如图,在矩形ABCD中,AB=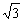 ,BC=a,又PA⊥平面ABCD,PA=4.
(1)若在边BC上存在一点Q,使PQ⊥QD,求a的取值范围;
(2)当BC上存在唯一点Q,使PQ⊥QD时,求异面直线AQ与PD所成角的大小;
(3)若a=4,且PQ⊥QD,求二面角A-PD-Q的大小.
,BC=a,又PA⊥平面ABCD,PA=4.
(1)若在边BC上存在一点Q,使PQ⊥QD,求a的取值范围;
(2)当BC上存在唯一点Q,使PQ⊥QD时,求异面直线AQ与PD所成角的大小;
(3)若a=4,且PQ⊥QD,求二面角A-PD-Q的大小.
解:
(1)、以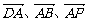 为x、y、z轴建立空间直角坐标系,则
为x、y、z轴建立空间直角坐标系,则
B(0,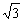 ,0),C(-a,
,0),C(-a,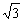 ,0),D(-a,0,0),P(0,0,4)
,0),D(-a,0,0),P(0,0,4)
设Q(t,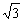 ,0),则
,0),则 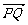 =(t,
=(t,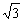 ,-4),
,-4),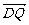 =(t+a,
=(t+a,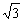 ,0)
∵PQ⊥QD,∴
,0)
∵PQ⊥QD,∴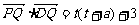 =0 即t2+at+3=0 ①
∴△=a2-12≥0 Þ a≥2
=0 即t2+at+3=0 ①
∴△=a2-12≥0 Þ a≥2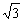 .
.
(2)、∵BC上存在唯一点Q,使PQ⊥QD,
∴△=a2-12=0 Þ a=2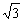 ,t=-
,t=-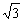
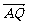 =(-
=(-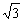 ,
,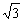 ,0) ,
,0) ,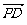 =(-2
=(-2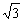 ,0,-4)
∴cos
,0,-4)
∴cos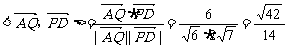 故异面直线AQ与PD所成角为arccos
故异面直线AQ与PD所成角为arccos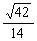 .
.
(3)、过Q作QM∥CD交AD于M,则QM⊥AD,M(t,0,0) ∵PA⊥平面ABCD,∴PA⊥QM,又QM⊥AD,∴QM⊥平面PAD 过M作MN⊥PD于N,连结NQ,由三垂线定理知QN⊥PD ∴∠MNQ是二面角A-PD-Q的平面角
设N (m,0,n),则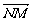 =(t-m,0,-n),
=(t-m,0,-n),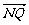 =(t-m,
=(t-m,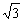 ,-n)
,-n)
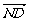 =(-4-m,0,-n) ∵MN⊥PD,ND、PD共线,∴
=(-4-m,0,-n) ∵MN⊥PD,ND、PD共线,∴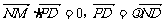
得:m+n-t=0,m-n=4 ② 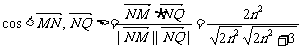
由①得:t=-1或t=-3,由②得:n=2+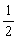 t
t
当t=-1时,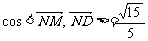 ,当t=-3时,
,当t=-3时,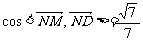
∴二面角A-PD-Q的大小为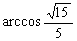 或
或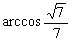 .
.
21、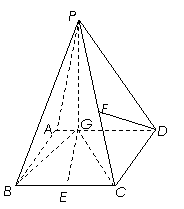 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且PG=4,
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且PG=4,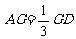 ,BG⊥GC,GB=GC=2,E是BC的中点.
,BG⊥GC,GB=GC=2,E是BC的中点.
(1)求异面直线GE与PC所成的角;
(2)求点D到平面PBG的距离;
(3)若F点是棱PC上一点,且DF⊥GC,求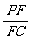 的值.
的值.
解:(1)解:以G点为原点,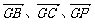 为x轴、y轴、z轴建立空间直角坐标系,
为x轴、y轴、z轴建立空间直角坐标系,
则B(2,0,0),C(0,2,0),P(0,0,4), 故E(1,1,0) 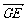 =(1,1,0),
=(1,1,0),
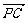 =(0,2,4)
=(0,2,4) 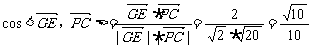
∴GE与PC所成的角为arccos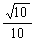 .
.
(2)解:平面PBG的单位法向量n=(0,±1,0) ∵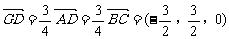
∴点D到平面PBG的距离为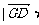 n |=
n |=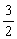
(3)解:设F(0,y,z),则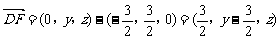
∵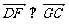 ,∴
,∴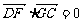 , 即
, 即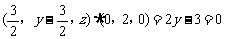 ,∴
,∴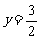 又
又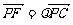 ,即(0,
,即(0,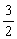 ,z-4)=λ(0,2,-4),∴z=1,
,z-4)=λ(0,2,-4),∴z=1,
故F(0,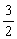 ,1)
,1) 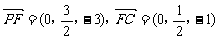 ,∴
,∴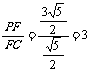
20、如图,已知点E是棱长为1的正方体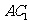 的棱
的棱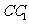 的中点,则点C到 平面
的中点,则点C到 平面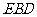 的距离等于
。
的距离等于
。
19、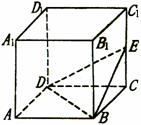 一个正方体的棱长为2,将八个直径各为1的球放进去之后,正中央空间能放下的最大的球的直径为
.
一个正方体的棱长为2,将八个直径各为1的球放进去之后,正中央空间能放下的最大的球的直径为
.
18、
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com