
4.3-4.4间的频数为100×0.1×0.1=1.
3.某校数学教研组为了解学生学习数学的情况,采用分层抽样的方法从高一600人、高二680人、高三720人中,抽取50人进行问卷调查,则高一、高二、高三抽取的人数分别是 ( )
A.15,16,19 B.15,17,18 C.14,17,19 D.15,16,20
解析:分层抽样要求每层中每个个体被抽到的概率均相等,据题意中每个个体被抽到的概率为=,故高一、高二和高三分别被抽取的人数为600×=15,680×=17,720×=18.
答案:B
4对于给定的两个变量的统计数据,下列说法正确的是 ( )
A.都可以分析出两个变量的关系
B.都可以用一条直线近似地表示两者的关系
C.都可以作出散点图
D.都可以用确定的表达式表示两者的关系
解析:给出一组样本数据,总可以作出相应的散点图,但不一定能分析出两个变量的关系,更不一定符合线性相关或有函数关系.
答案:C
5为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如下图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a,b的值分别为 ( )
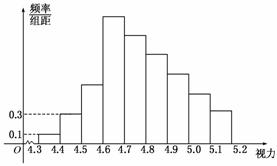
A.0.27,78 B.0.27,83 C.2.7,78 D.2.7,83
解析:由频率分布直方图知组矩为0.1.
2.如图是根据《山东统计年鉴2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字.从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为 ( )
A.304.6 B.303.6 C.302.6 D.301.6
解析:由已知得平均数
=
=303.6.
答案:B
1.某地区共有10万户居民,该地区城市住户与农村住户之比为4∶6,根据分层抽样方法,调查了该地区1 000户居民冰箱拥有情况,调查结果如下表所示,那么可以估计该地区农村住户中无冰箱的总户数约为 ( )
|
|
城市 |
农村 |
|
有冰箱 |
356(户) |
440(户) |
|
无冰箱 |
44(户) |
160(户) |
A.1.6万户 B.4.4万户 C.1.76万户 D.0.24万户
解析:由分层抽样按比例抽取可得×100 000=16 000.
 答案:A
答案:A
21. (本小题满分14分)一个质地均匀的正四面体(侧棱长与底面边长相等的正三棱锥)骰子四个面上分别标有1,2,3,4这四个数字,抛掷这颗正四面体骰子,观察抛掷后能看到的数字.
(1)若抛掷一次,求能看到的三个面上数字之和大于6的概率;
(2)若抛掷两次,求两次朝下面上的数字之积大于7的概率;
(3)若抛掷两次,以第一次朝下面上的数字为横坐标a,第二次朝下面上的数字为纵坐标b,求点(a,b)落在直线x-y=1下方的概率.
解:(1)记事件“抛掷后能看到的数字之和大于6”为A,抛掷这颗正四面体骰子,抛掷后能看到的数字构成的集合有{2,3,4},{1,3,4},{1,2,4},{1,2,3},共有4种情形,其中,能看到的三面数字之和大于6的有3种,则P(A)=.
(2)记事件“抛掷两次,两次朝下面上的数字之积大于7”为B,两次朝下面上的数字构成的数对共有16种情况,其中能够使得数字之积大于7的为(2,4),(4,2),(3,3),(3,4),(4,3),(4,4)共6种,则P(B)==.
(3)记事件“抛掷后点(a,b)在直线x-y=1的下方”为C,要使点(a,b)在直线x-y=1的下方,则需b<a-1,当b=1时,a=3或4;当b=2时,a=4.
则所求的概率P(C)=.
20. (本小题满分13分)甲、乙两人玩一种游戏,每次由甲、乙各出1到5根手指,若和为偶数算甲赢,否则算乙赢.
(1)若以A表示和为6的事件,求P(A);
(2)现连玩三次,若以B表示甲至少赢一次的事件,C表示乙至少赢两次的事件,试问B与C是否为互斥事件?为什么?
(3)这种游戏规则公平吗?试说明理由.
解:(1)基本事件空间与点集S={(x,y)|x∈N*,y∈N*,1≤x≤5,1≤y≤5}中的元素一一对应.
因为S中点的总数为5×5=25(个),所以基本事件总数为n=25.
事件A包含的基本事件数共5个:
(1,5)、(2,4)、(3,3)、(4,2)、(5,1),
所以P(A)==.
(2)B与C不是互斥事件,因为事件B与C可以同时发生,如甲赢一次,乙赢两次.
(3)这种游戏规则不公平.由(1)知和为偶数的基本事件为13个,所以甲赢的概率为,乙赢的概率为,
所以这种游戏规则不公平.
19. (本小题满分12分)在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中有放回地先后抽得两张卡片的标号分别为x、y,记z=|x-2|+|y-x|.求z的所有可能的取值,并求出z取相应值时的概率.
解:z的所有可能取值为0,1,2,3.
当z=0时,只有x=2,y=2这一种情况,
当z=1时,有x=1,y=1或x=2,y=1或x=2,y=3或x=3,y=3四种情况,
当z=2时,有x=1,y=2或x=3,y=2两种情况,
当z=3时,有x=1,y=3或x=3,y=1两种情况,
∵有放回地抽两张卡片的所有情况有9种.
∴P(z=0)=,P(z=1)=,P(z=2)=,
P(z=3)=.
18. (本小题满分12分)投掷一个质地均匀的、每个面上标有一个数字的正方体玩具,它的六个面中,有两个面标的数字是0,两个面标的数字是2,两个面标的数字是4,将此玩具连续抛掷两次,以两次朝上一面出现的数字分别作为点P的横坐标和纵坐标.
(1)求点P落在区域C:x2+y2≤10内的概率;
(2)若以落在区域C上的所有点为顶点作面积最大的多边形区域M,在区域C上随机撒一粒豆子,求豆子落在区域M上的概率.
解: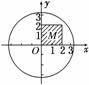 (1)点P的坐标有:(0,0),(0,2),(0,4),(2,0),(2,2),(2,4),(4,0),
(1)点P的坐标有:(0,0),(0,2),(0,4),(2,0),(2,2),(2,4),(4,0),
(4,2),(4,4),共9种,其中落在区域C:x2+y2≤10上的点P的坐标有:
(0,0),(0,2),(2,0),(2,2),共4种.故点P落在区域C:x2+y2≤10内 的
概率为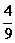 .
.
(2)区域M为一边长为2的正方形,其面积为4,区域C的面积为10π,则豆子落在区域M上的概率为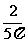 .
.
17.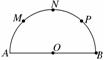 (本小题满分12分)如图,已知AB是半圆O的直径,AB=8,M、N、
(本小题满分12分)如图,已知AB是半圆O的直径,AB=8,M、N、
P是将半圆圆周四等分的三个分点.
(1)从A、B、M、N、P这5个点中任取3个点,求这3个点组成直角
三角形的概率;
(2)在半圆内任取一点S,求三角形SAB的面积大于8的概率.
解:(1)从A、B、M、N、P这5个点中任取3个点,一共可以组成10个三角形:ABM、ABN、ABP、AMN、AMP、ANP、BMN、BMP、BNP、MNP,其中是直角三角形的只有ABM、ABN、ABP 3个,
 所以这3个点组成直角三角形的概率P=.
所以这3个点组成直角三角形的概率P=.
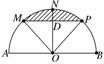
(2)连结MP,取线段MP的中点D,则OD⊥MP,
易求得OD=2,
当S点在线段MP上时,S△ABS=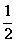 ×2
×2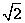 ×8=8
×8=8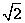 ,
,
所以只有当S点落在阴影部分时,三角形SAB面积才能大于8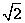 ,而
,而
S阴影=S扇形OMP-S△OMP=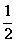 ×
×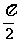 ×42-
×42-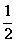 ×42=4π-8,
×42=4π-8,
所以由几何概型公式得三角形SAB的面积大于8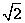 的概率P=
的概率P=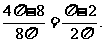
16.(本小题满分12分)设A={(x,y)|1≤x≤6,1≤y≤6,x,y∈N*}.
(1)求从A中任取一个元素是(1,2)的概率;
(2)从A中任取一个元素,求x+y≥10的概率;
解:(1)设从A中任取一个元素是(1,2)的事件为B,则P(B)=,所以从A中任取一个元素是(1,2)的概率为.
(2)设从A中任取一个元素,x+y≥10的事件为C,则有(4,6),(6,4),(5,5),(5,6),(6,5),(6,6)共6种情况,
于是P(C)=,
所以从A中任取一个元素,x+y≥10的概率为.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com