
5.α为第四象限角,则2α在 .
4.终边在第一或第三象限角的集合是 .
3.若α与β的终边互为反向延长线,则有( )
A.α=β+180° B.α=β-180°
C.α=-β D.α=β+(2k+1)180°,k∈Z
2.若α是第四象限角,则180°-α是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
1.若A={α|α=k·360°,k∈Z};
B={α|α=k·180°,k∈Z};
C={α|α=k·90°,k∈Z},则下列关系中正确的是( )
A.A=B=C
B.A=B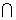 C
C
C.A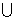 B=C
D.A
B=C
D.A B
B C
C
例1写出终边在y轴上的角的集合(用0到360度的角表示).
解:∵ 在0°-360°间,终边在y轴的正半轴上的角为90°,终边在y轴的负半轴上的角为270°,
∴终边在y正半轴、负半轴上所有角分别是:
S1={a|a=k×360°+90°,kÎZ};S2={a|a=k×360°+270°,kÎZ}
探究:怎么将二者写成统一表达式?
∵S1={a|a=k×360°+90°,kÎZ}={a|a=2k×180°+90°,kÎZ};
S2={a|a=k×360°+270°,kÎZ}={a|a=2k×180°+180°+90°,kÎZ}
={a|a=(2k+1)×180°+90°,kÎZ};
∴终边在y轴上的角的集合是:
S=S1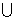 S2={a|a=2k×180°+90°,kÎZ}
S2={a|a=2k×180°+90°,kÎZ}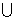 {a|a=(2k+1)×180°+90°,kÎZ}
{a|a=(2k+1)×180°+90°,kÎZ}
={a|a=180°的偶数倍+90°,kÎZ}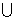 {a|a=180°的奇数倍+90°,kÎZ}
{a|a=180°的奇数倍+90°,kÎZ}
={a|a=180°的整数倍+90°,kÎZ}
={a|a=n×180°+90°,nÎZ}
引申:写出所有轴上角的集合

{a|a=k×360°, kÎZ} {a|a=k×360°+180°,kÎZ} {a|a=k×180°,kÎZ}

{a|a=k×360°+90°,kÎZ} {a|a=k×360°+270°,kÎZ} {a|a=k×180°+90°,kÎZ}
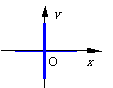

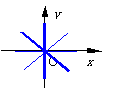
{a|a=k×90°, kÎZ} {a|a=k×90°+45°, kÎZ} {a|a=k×45°, kÎZ}
(最后两个可以根据实际情况处理)
例2.用集合的形式表示象限角
第一象限的角表示为{a|k×360°<a<k×360°+90°,(kÎZ)};
第二象限的角表示为{a|k×360°+90°<a<k×360°+180°,(kÎZ)};
第三象限的角表示为{a|k×360°+180°<a<k×360°+270°,(kÎZ)};
第四象限的角表示为{a|k×360°+270°<a<k×360°+360°,(kÎZ)};
或{a|k×360°-90°<a<k×360°,(kÎZ)}
例3 写出角的终边在图中阴影区域内的角的集合(不包括边界)
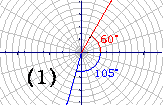
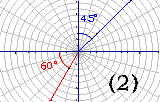
解:.(1){α|60°+k·360°<α<255°+k·360°,k∈Z}
(2){α|-120°+k·360°<α<45°+k·360°,k∈Z}
例4 已知a是第二象限角,问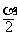 是第几象限角?2a是第几象限角?分别加以说明
是第几象限角?2a是第几象限角?分别加以说明
解:∵a在第二象限,∴k×360°+90°<a<k×360°+180°,kÎZ
于是, k×180°+45°<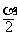 <k×180°+90°,
∵kÎZ, ∴k=2n或k=2n+1
<k×180°+90°,
∵kÎZ, ∴k=2n或k=2n+1
当k=2n时,n×360°+45°<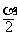 <n×360°+90°,
∴
<n×360°+90°,
∴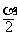 在第一象限;
在第一象限;
当k=2n+1时,n×360°+225°<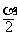 <n×360°+270°,
∴
<n×360°+270°,
∴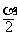 在第三象限;
在第三象限;
∴当a在第二象限时,∴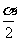 可能在第一象限,也可能在第三象限
可能在第一象限,也可能在第三象限
类似地,2a可能在第三、四象限或y轴负半轴上
3.终边相同的角
结论:所有与a终边相同的角连同a在内可以构成一个集合:
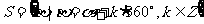
即:任何一个与角a终边相同的角,都可以表示成角a与整数个周角的和
⑷注意以下四点:
(1)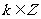
(2) a是任意角;
(3)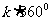 与a之间是“+”号,
与a之间是“+”号,
如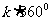 -30°,应看成
-30°,应看成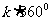 +(-30°);
+(-30°);
(4)终边相同的角不一定相等,但相等的角,终边一定相同,终边相同的角有无数多个,它们相差360°的整数倍.
2.“象限角”
角的顶点合于坐标原点,角的始边合于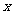 轴的正半轴,这样一来,角的终边落在第几象限,我们就说这个角是第几象限的角(角的终边落在坐标轴上,则此角不属于任何一个象限)
轴的正半轴,这样一来,角的终边落在第几象限,我们就说这个角是第几象限的角(角的终边落在坐标轴上,则此角不属于任何一个象限)
1.角的概念的推广
⑴“旋转”形成角
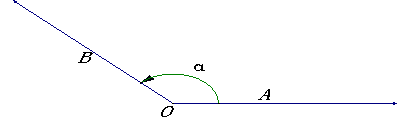
一条射线由原来的位置OA,绕着它的端点O按逆时针方向旋转到另一位置OB,就形成角α.旋转开始时的射线OA叫做角α的始边,旋转终止的射线OB叫做角α的终边,射线的端点O叫做角α的顶点.
⑵.“正角”与“负角”“0角”
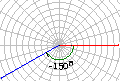
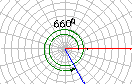
我们把按逆时针方向旋转所形成的角叫做正角,把按顺时针方向旋转所形成的角叫做负角,如图,以OA为始边的角α=210°,β=-150°,γ=660°,
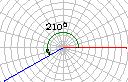
特别地,当一条射线没有作任何旋转时,我们也认为这时形成了一个角,并把这个角叫做零角.记法:角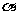 或
或 可以简记成
可以简记成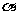

⑶意义
用“旋转”定义角之后,角的范围大大地扩大了
3° 还有零角 一条射线,没有旋转
角的概念推广以后,它包括任意大小的正角、负角和零角.
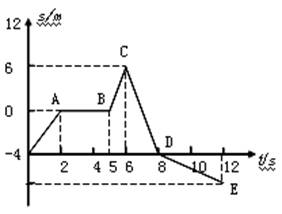
15.某物体的位移图象如图所示,若规定向东为正方向,试求物体在OA、AB、BC、CD、DE各阶段的速度。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com