4．产生明显衍射的条件：障碍物或孔的尺寸可以跟光的波长相比或比光的波长小．

小结：光的干涉条纹和衍射条纹都是光波叠加的结果，但存在明显的区别：

单色光的衍射条纹与干涉条纹都是明暗相间分布，但衍射条纹中间亮纹最宽，两侧条纹逐渐变窄变暗，干涉条纹则是等间距，明暗亮度相同。 白光的衍射条纹与干涉条纹都是彩色的。

[例5]某同学以线状白炽灯为光源，利用游标卡尺两脚间形成的狭缝观察光的衍射现象后，总结出以下几点，你认为正确的是

A.若狭缝与灯泡平行，衍射条纹与狭缝平行

B.若狭缝与灯泡垂直，衍射条纹与狭缝垂直

C.衍射条纹的疏密程度与狭缝的宽度有关

D.衍射条纹的间距与光的波长有关　　　 [答案] ACD

[例6]平行光通过小孔得到的衍射图样和泊松亮斑比较，下列说法中正确的有　　　　

A.在衍射图样的中心都是亮斑　　　　

B.泊松亮斑中心亮点周围的暗环较宽

C.小孔衍射的衍射图样的中心是暗斑，泊松亮斑图样的中心是亮斑

D.小孔衍射的衍射图样中亮、暗条纹间的间距是均匀的，泊松亮斑图样中亮、暗条纹间的间距是不均匀的　　　

解：从课本上的图片可以看出：A、B选项是正确的，C、D选项是错误的。

3．　 各种不同形状的障碍物都能使光发生衍射。

2．泊松亮斑：当光照到不透光的极小圆板上时，在圆板的阴影中心出现的亮斑。当形成泊松亮斑时，圆板阴影的边缘是模糊的，在阴影外还有不等间距的明暗相间的圆环。

1．　　　 光的衍射现象是光离开直线路径而绕到障碍物阴影里的现象．

2.全反射应用与棱镜

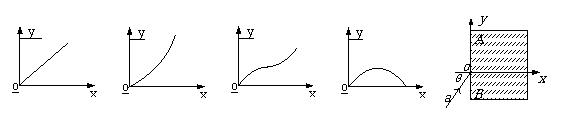[例14] 如图所示，AB为一块透明的光学材料左侧的端面。建立直角坐标系如图，设该光学材料的折射率沿y轴正方向均匀减小。现有一束单色光a从原点O以某一入射角θ由空气射入该材料内部，则该光线在该材料内部可能的光路是下图中的哪一个

A.　　　　　　 B.　　　　　　 C.　　　　　　 D.　　　　　　　　

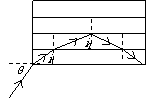解：如图所示，由于该材料折射率由下向上均匀减小，可以设想将它分割成折射率不同的薄层。光线射到相邻两层的界面时，如果入射角小于临界角，则射入上一层后折射角大于入射角，光线偏离法线。到达更上层的界面时入射角逐渐增大，当入射角达到临界角时发生全反射，光线开始向下射去直到从该材料中射出。

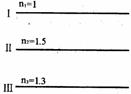[例15]如图所示是三种不同煤质叠放在一起，且界面互相平行．媒质l的折射率n₁＝l，媒质2的折射率n₂=1．5，媒质3的折射率n₃=1．3，现有一束单色光射到界面I上，则下列判断正确的是(　　　 )

A．该光束可能在界面I上发生全反射　　

B．该光束可能在界面Ⅱ上发生全反射　　

C．该光束可能在界面Ⅲ上发生全反射　　

D．该光束在三个界面上均不能发生全反射

　　 解析：光束是由媒质I而进入其它媒质的，由题意可知媒质I的折射率最小，入射角θ₁＜90．三个界面互相平行，那么在同一煤质中的折射角一定等于入射角．由折射的知识可得：n₁sinθ₁= n₂sinθ₂= n₃sinθ₃，而n₂＞n₃＞n₁，所以，θ₂＜θ₃＜θ₁＜90⁰，也就是说在三个界面上均不会发生全反射．

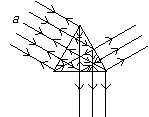[例17] 如图所示，一束平行单色光a垂直射向横截面为等边三角形的棱镜的左侧面，棱镜材料的折射率是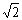。试画出该入射光射向棱镜后所有可能的射出光线。

解：由折射率为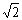得全反射临界角是45°。光线从左侧面射入后方向不发生改变，射到右侧面和底面的光线的入射角都是60°，大于临界角，因此发生全反射。反射光线分别垂直射向底面和右侧面。在底面和右侧面同时还有反射光线。由光路可逆知，它们最终又从左侧面射出。所有可能射出的光线如图所示。

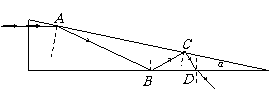
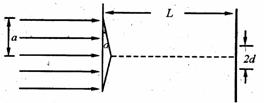[例18]平行光束垂直射在等腰玻璃棱镜的底面上，如图所示．如果在离棱镜距离L＝100cm处放一个屏M。在屏幕中央形成宽为2 d=1cm的暗斑．求棱镜的折射角α。玻璃的拆射率n=1．57，底面大小为2a＝5 cm。

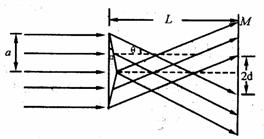　 解析：作出这束平行光经过玻璃棱镜后的光路图如图所示．从图中的光路图可知，棱镜的上半部的折射光线与入射光线的夹角为θ，入射角为α，折射角为β(图中没有画出)，由于α很小，由折射定律可得m=sinβ/sinα＝β／α，

θ-β＝(n－l)而　 tgθ＝(a+d)／L=3×10^－2　

θ=3×10^－2rad　　

α＝θ／(n－l)＝3×10^－2／(1．57－1)rad＝5．26×10^－2rad=3⁰

试题展示

基础知识

规律方法

试题展示

1.边作图边计算

有关光的折射和全反射，在解题时首先要判断是否发生全反射，在确定未发生全反射的条件下，再根据折射定律确定入射角或折射角．要把计算和作图有机地结合起来，根据数据计算反射角、折射角，算一步画一步，画一步在根据需要算一步。作图要依据计算结果，力求准确。

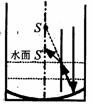[例11]如图所示，一圆柱形容器的底部有一凹面镜，其主轴与圆柱形容器的轴线重合，一点光源S射向凹面镜的光线，经凹面镜反射平行于主轴，当往容器中注入水后，水面在点光源与凹面镜之间，要使点光源S射向凹面镜的光线，以凹镜反射后互相平行，则点光源就沿主轴．

　　 A．适当提高； B．适当降低； C．不动 ；D．无法确定移动方向；

解析：点光源射向水面的光线要发生一次折射，再射到凹面镜上发生反射，反射的光线互相平行．由光路可逆，设光线平行于主轴射向凹面镜，在凹面镜反射后射向水面，在水面上发生折射，由图可知，S^/在S的下方，说明了点光源S应适当降低．

[例12] 直角三棱镜的顶角α=15°, 棱镜材料的折射率n=1.5，一细束单色光如图所示垂直于左侧面射入，试用作图法求出该入射光第一次从棱镜中射出的光线。

解：由n=1.5知临界角大于30°小于45°，边画边算可知该光线在射到A、B、C、D各点时的入射角依次是75°、60°、45°、30°，因此在A、B、C均发生全反射，到D点入射角才第一次小于临界角，所以才第一次有光线从棱镜射出。

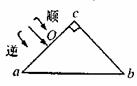[例10]abc为全反射棱镜，它的主截面是等腰直角三角形，如图23-3所示。一束白光垂直入射到ac面上，在ab面上发生全反射，若光线入射点O的位置不变，改变光线的入射方向(不考虑bc面反射的光线)(　　 )

A、使入射光线按图所示的顺时针方向逐渐偏转，如果有色光射出ab面，则红光将首先射出。

B、使入射光按图中所示的顺时针方向逐渐偏转，如果有色光射出ab面，则紫光将首先射出

C、使入射光按图中所示的逆时针方向逐渐偏转，红光将首先射出ab面

D、使入射光按图中所示的逆时针方向逐渐偏转，紫光将首先射出ab面

解答：白光是由红到紫七种色光组成，同一种介质对它们的折射率，从红光到紫光逐渐增大。从同一介质射向空气发生全反射的临界角不同。由公式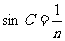，n越小，C越大。红光折射率最小，则临界角最大。光垂直入射ac面，在ab面发生全反射，则临界角c≤45°，紫光折射率最大，则临界角最小。当入射光沿顺时针方向偏转时，通过ac面折射后，射到ab面的入射角减小，首先小到红光临界角以下，红光先射出ab面。当入射光沿逆时针方向偏转时，通过ac面折射后，射到ab面的入射角增大，不可能有光从ab面射出。

几何光学是借用“几何”知识来研究光的传播问题的，而光的传播路线又是由光的基本传播规律来确定。所以，对于几何光学问题，只要能够画出光路图，剩下的就只是“几何问题”了。而几何光学中的光路通常有如下两类：

(1)“成像光路”--一般来说画光路应依据光的传播规律，但对成像光路来说，特别是对薄透镜的成像光路来说，则是依据三条特殊光线来完成的。这三条特殊光线通常是指：平行于主轴的光线经透镜后必过焦点；过焦点的光线经透镜后必平行于主轴；过光心的光线经透镜后传播方向不变。

(2)“视场光路”--即用光路来确定观察范围。这类光路一般要求画出所谓的“边缘光线”，而一般的“边缘光线”往往又要借助于物点与像点的一一对应关系来帮助确定。

规律方法　　 一. 用光的折射解释自然现象

现象一:星光闪烁与光折射

由于重力的影响，包围地球的大气密度随高度而变化；另外，由于气候的变化，大气层的各处又在时刻不断地变化着，这种大气的物理变化叫做大气的抖动．由于大气的抖动便引起了空气折射率的不断变化．我们观望某一星星时，星光穿过大气层进入眼睛，于是看到了星光．之后由于大气的抖动，使空气折射率发生变化，星光传播的路径便发生了改变，这时星光到达另一地点，我们站在原来的地方就看不见它的光了，便形成一次闪烁．大气的抖动是时刻不停的，并与气候密切相关．一般大气抖动明显地大气折射率而形成一次闪烁的时间间隔是1-4秒，所以，我们观望星空时，看到的星光是闪烁的了

现象二:蓝天、红日与光散射

光在传播过程中，遇到两种均匀媒质的分界面时，会产生反射和折射现象．但当光在不均匀媒介质中传播时，情况就不同了．由于一部分光线不能直线前进，就会向四面八方散射开来，形成光的散射现象．地球周围由空气形成的大气层，就是这样一种不均匀媒质．因此，我们看到的天空的颜色，实际上是经大气层散射的光线的颜色．科学家的研究表明，大气对不同色光的散射作用不是“机会均等”的，波长短的光受一的散射最厉害．当太阳光受到大气分子散射时，波长较短的蓝光被散射得多一些．由于天空中布满了被散射的蓝光，地面上的人就看到天空呈现出蔚蓝色．空气越是纯净、干燥，这种蔚蓝色就越深、越艳．如果天空十分纯净，没有大气和其他微粒的散射作用，我们将看不到这种璀璨的蓝色．比如在2万米以上的高空，空气气体分子特别稀薄，散射作用已完全消失，天空也会变得暗淡．

同样道理，旭日初升或日落西山时，直接从太阳射来的光所穿过的大气层厚度，比正午时直接由太阳射击来的光所穿过的大气层厚度要厚得多．太阳光在大气层中传播的距离越长，被散射掉的短波长的蓝光就越多，长波长的红光的比例也显著增多．最后到达地面的太阳光，它的红色万分也相对增加，因此，才会出现满天红霞和血红夕阳．实际上，发光的太阳表面的颜色却始终没有变化．

现象三:光在大气中的折射

光在到达密度不同的两层大气的分界面时，会发生光的折射．气象学告诉我们，空气的密度的大小主要受气压和气温两个条件的影响．气压指得是单位面积空气柱的重量．大气层包围在地球表面，因此在大气层的低层气压较高，越向上气压越低．气压高则空气密度大，气压低则空气密度小．因此，正常情况下，总是贴近地面的空气密度最大，越向上空气密度越小．温度对空气密度的影响和气压则刚好相反．气温越高，空气的体积越膨胀，空气的密度越小；温度越低，空气收缩，则空气的密度变大．一般越接近地面温度越高(逆温层是个例外)．

根据实测所得，在大多数情况下，温度的上下差别不是太大，而气压上下的差别却很显著，因此气压对空气密度的垂直分布所产生的影响远比气温的影响大，这就使得空气密度经常是越向上越小的(当然减小的情况并不是一成不变的)．

由于地球上空气的密度随高度的变化，折射率随密度减小而正比例地减小，因此光在大气中传播时，通过一层层密度不同的大气，在各层的分界面处会发生折射，使光线不沿直线传播而是变弯曲，这样当太阳和其他星体的光线进入大气以后，光线就会拐弯，这种现象称天文折射，这使在地面观测得的天体视位置S'比实际位置S高．

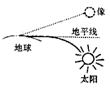
[例9]假设地球表面不存在气层，那么人们观察到日出时刻与实际存在大气层的情况相比(　　 )

A、将提前　　　 B、将延后　　　

C、在某些地区将提前，在另一些地区将延后　　　 D、不变

分析：注意到大气层不均匀的特性

解答：由几何光学知识可知，有大气层时，由于地表大气层不均匀，太阳光线经大气折射后向下弯曲，如图所示，地球上观察者看到日出的太阳要比实际位置高，也就是当太阳还在地平线以下时就可以看到太阳的像；而没有大气层时，太阳光线沿直线传播，当太阳在地平线以下时是看不到太阳的。故有大气层时可提前看到日出。

物点发出的发散光束照射到镜面上并经反射或折射后，如会聚于一点，则该点即为物点经镜面所成的实像点；如发散，则其反向延长后的会聚点即为物点经镜面所成的虚像点。因此，判断某光学镜是否能成实(虚)像，关键看发散光束经该光学镜的反射或折射后是否能变为会聚光束(可能仍为发散光束)。

(1)平面镜的反射不能改变物点发出的发散光束的发散程度，所以只能在异侧成等等大的、正立的虚像。

(2)凹透镜的折射只能使物点发出的发散光束的发散程度提高，所以只能在同侧成缩小的、正立的虚像。

(3)凸透镜的折射既能使物点发出的发散光束仍然发散，又能使物点发出的发散光束变为聚光束，所以它既能成虚像，又能成实像。

(1)光束经平面镜反射后，其会聚(或发散)的程度将不发生改变。这正是反射定律中“反射角等于入射角”及平面镜的反射面是“平面”所共同决定的。

(2)光束射向三棱镜，经前、后表面两次折射后，其传播光路变化的特征是：向着底边偏折，若光束由复色光组成，由于不同色光偏折的程度不同，将发生所谓的色散现象。

(3)光束射向前、后表面平行的透明玻璃砖，经前、后表面两次折射后，其传播光路变化的特征是；传播方向不变，只产生一个侧移。

(4)光束射向透镜，经前、后表面两次折射后，其传播光路变化的特征是：凸透镜使光束会聚，凹透镜使光束发散。