
(四)巩固练习:
1.函数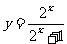 的值域为 .
的值域为 .
2.若函数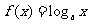 在
在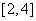 上的最大值与最小值之差为2,则
上的最大值与最小值之差为2,则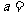 .
.
(二)(配方法)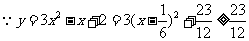 ,
,
∴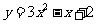 的值域为
的值域为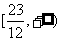 .
.
改题:求函数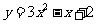 ,
,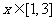 的值域.
的值域.
解:(利用函数的单调性)函数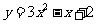 在
在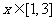 上单调增,
上单调增,
∴当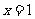 时,原函数有最小值为
时,原函数有最小值为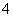 ;当
;当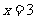 时,原函数有最大值为
时,原函数有最大值为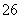 .
.
∴函数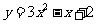 ,
,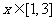 的值域为
的值域为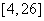 .
.
(2)求复合函数的值域:设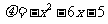 (
( ),则原函数可化为
),则原函数可化为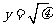 .
.
又∵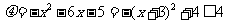 ,∴
,∴ ,故
,故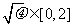 ,
,
∴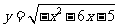 的值域为
的值域为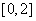 .
.
(3)(法一)反函数法: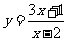 的反函数为
的反函数为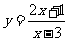 ,其定义域为
,其定义域为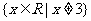 ,
,
∴原函数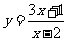 的值域为
的值域为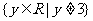 .
.
(法二)分离变量法: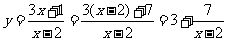 ,
,
∵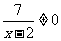 ,∴
,∴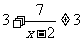 ,
,
∴函数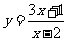 的值域为
的值域为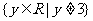 .
.
(4)换元法(代数换元法):设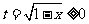 ,则
,则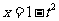 ,
,
∴原函数可化为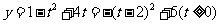 ,∴
,∴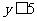 ,
,
∴原函数值域为 .
.
说明:总结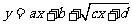 型值域,变形:
型值域,变形: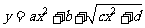 或
或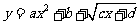
(5)三角换元法:∵ ,∴设
,∴设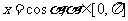 ,
,
则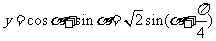
∵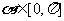 ,∴
,∴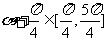 ,∴
,∴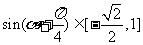 ,∴
,∴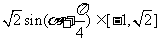 ,
,
∴原函数的值域为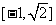 .
.
(6)数形结合法: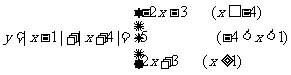 ,∴
,∴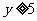 ,∴函数值域为
,∴函数值域为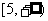 .
.
(7)判别式法:∵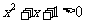 恒成立,∴函数的定义域为
恒成立,∴函数的定义域为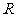 .
.
由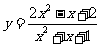 得:
得: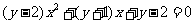 ①
①
①当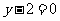 即
即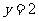 时,①即
时,①即 ,∴
,∴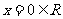
②当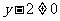 即
即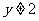 时,∵
时,∵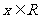 时方程
时方程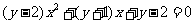 恒有实根,
恒有实根,
∴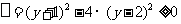 ,
, ∴
∴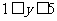 且
且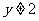 ,
,
∴原函数的值域为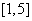 .
.
(8)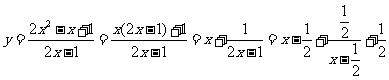 ,
,
∵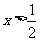 ,∴
,∴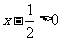 ,∴
,∴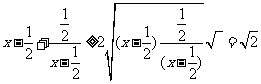 ,当且仅当
,当且仅当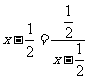 时,即
时,即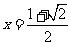 时等号成立.∴
时等号成立.∴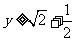 ,∴原函数的值域为
,∴原函数的值域为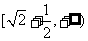 .
.
(9)(法一)方程法:原函数可化为: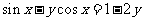 ,
,
∴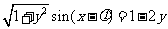 (其中
(其中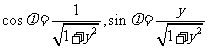 ),
),
∴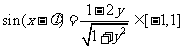 ,∴
,∴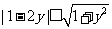 ,∴
,∴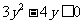 ,∴
,∴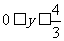 ,
,
∴原函数的值域为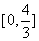 .
.
(法二)数形结合法:可看作求点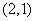 与圆
与圆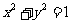 上的点的连线的斜率的范围,解略.
上的点的连线的斜率的范围,解略.
例2.若关于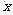 的方程
的方程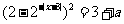 有实数根,求实数
有实数根,求实数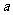 的取值范围.
的取值范围.
解:原方程可化为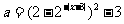 ,
,
令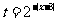 ,则
,则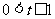 ,
,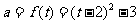 ,又∵
,又∵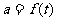 在区间
在区间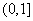 上是减函数,
上是减函数,
∴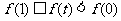 ,即
,即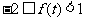 ,
,
故实数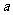 的取值范围为:
的取值范围为: .
.
例3.某化妆品生产企业为了占有更多的市场份额,拟在2003年度进行一系列的促销活动.经过市场调查和测算,化妆品的年销量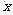 万件与年促销费用
万件与年促销费用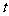 万元
万元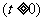 之间满足:
之间满足: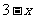 与
与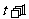 成反比例;如果不搞促销活动,化妆品的年销量只能是1万件.
成反比例;如果不搞促销活动,化妆品的年销量只能是1万件.
已知2003年,生产化妆品的固定投入为3万元,每生产1万件化妆品需再投入32万元.当将每件化妆品的售价定为“年平均每件成本的150%”与“年平均每件所占促销费的一半”之和,则当年产销量相等.
(1)将2003年的年利润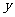 万元表示为年促销费
万元表示为年促销费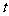 万元的函数;
万元的函数;
(2)该企业2003年的促销费投入多少万元时,企业的年利润最大?
(注:利润=收入-生产成本-促销费)
解:(1)由题设知: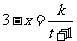 ,且
,且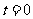 时,
时,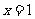 ,∴
,∴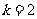 ,即
,即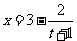 ,
,
∴年生产成本为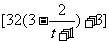 万元,年收入为
万元,年收入为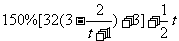 .
.
∴年利润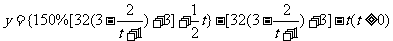 ,
,
∴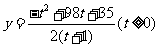 .
.
(2)由(1)得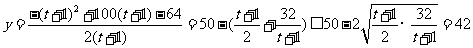 ,
,
当且仅当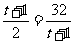 ,即
,即 时,
时, 有最大值
有最大值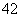 .
.
∴当促销费定为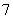 万元时,
万元时,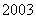 年该化妆品企业获得最大利润.
年该化妆品企业获得最大利润.
(三)例题分析:
例1.求下列函数的值域:
(1)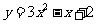 ; (2)
; (2)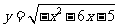 ; (3)
; (3)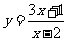 ;
;
(4)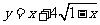 ; (5)
; (5)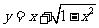 ; (6)
; (6)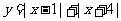 ;
;
(7)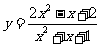 ; (8)
; (8)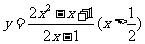 ; (9)
; (9)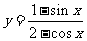 .
.
解:(1)(一)公式法(略)
(二)主要方法(范例分析以后由学生归纳):
求函数的值域的方法常用的有:直接法,配方法,判别式法,基本不等式法,逆求法(反函数法),换元法,图像法,利用函数的单调性、奇偶性求函数的值域等.
(一)主要知识:
1.函数的值域的定义;2.确定函数的值域的原则;3.求函数的值域的方法.
(四)巩固练习:
1.已知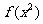 的定义域为
的定义域为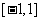 ,则
,则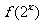 的定义域为
的定义域为 .
.
2.函数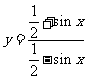 的定义域为
的定义域为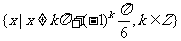 .
.
(三)例题分析:
例1.已知函数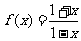 的定义域为
的定义域为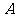 ,函数
,函数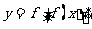 的定义域为
的定义域为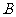 ,则
,则
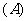
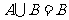
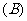
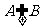
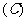
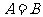
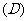
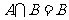 (
( 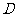 )
)
解法要点: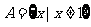 ,
,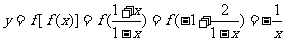 ,
,
令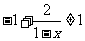 且
且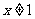 ,故
,故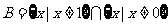 .
.
例2.(1)已知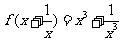 ,求
,求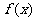 ;
;
(2)已知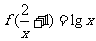 ,求
,求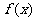 ;
;
(3)已知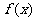 是一次函数,且满足
是一次函数,且满足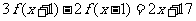 ,求
,求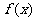 ;
;
(4)已知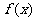 满足
满足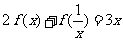 ,求
,求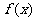 .
.
解:(1)∵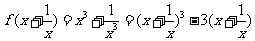 ,
,
∴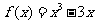 (
( 或
或 ).
).
(2)令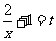 (
(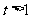 ),则
),则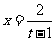 ,∴
,∴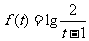 ,∴
,∴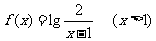 .
.
(3)设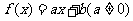 ,
,
则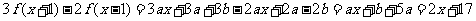 ,
,
∴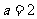 ,
,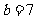 ,∴
,∴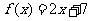 .
.
(4)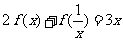 ①,
把①中的
①,
把①中的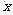 换成
换成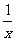 ,得
,得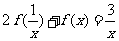 ②,
②,
①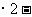 ②得
②得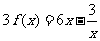 ,∴
,∴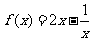 .
.
注:第(1)题用配凑法;第(2)题用换元法;第(3)题已知一次函数,可用待定系数法;第(4)题用方程组法.
例3.设函数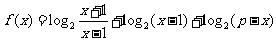 ,
,
(1)求函数的定义域;
解:(1)由 ,解得
,解得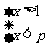 ①
①
当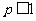 时,①不等式解集为
时,①不等式解集为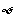 ;当
;当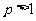 时,①不等式解集为
时,①不等式解集为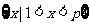 ,
,
∴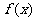 的定义域为
的定义域为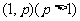 .
.
(二)主要方法:
1.求函数解析式的题型有:
(1)已知函数类型,求函数的解析式:待定系数法;
(2)已知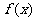 求
求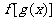 或已知
或已知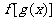 求
求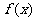 :换元法、配凑法;
:换元法、配凑法;
(3)已知函数图像,求函数解析式;
(4)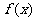 满足某个等式,这个等式除
满足某个等式,这个等式除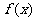 外还有其他未知量,需构造另个等式:解方程组法;
外还有其他未知量,需构造另个等式:解方程组法;
(5)应用题求函数解析式常用方法有待定系数法等.
2.求函数定义域一般有三类问题:
(1)给出函数解析式的:函数的定义域是使解析式有意义的自变量的取值集合;
(2)实际问题:函数的定义域的求解除要考虑解析式有意义外,还应考虑使实际问题有意义;
(3)已知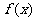 的定义域求
的定义域求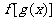 的定义域或已知
的定义域或已知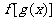 的定义域求
的定义域求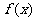 的定义域:
的定义域:
①掌握基本初等函数(尤其是分式函数、无理函数、对数函数、三角函数)的定义域;
②若已知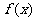 的定义域
的定义域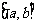 ,其复合函数
,其复合函数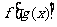 的定义域应由
的定义域应由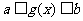 解出.
解出.
(一)主要知识:1.函数解析式的求解;2.函数定义域的求解.
(四)巩固练习:
1. 给定映射
给定映射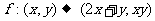 ,点
,点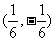 的原象是
的原象是
2.下列函数中,与函数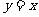 相同的函数是
(
相同的函数是
( 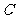 )
)
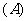
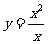
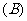
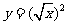
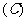
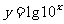
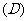
3.设函数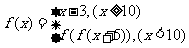 ,则
,则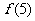 =
=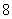 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com