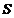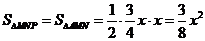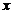∴ =．（0＜＜4）  ………………3分

∴ AN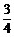＝x．   ……………2分

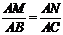∴ ，即．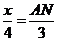

24．(本题满分12分)

解：（1）∵MN∥BC，∴∠AMN=∠B，∠ANM＝∠C．

  ∴ △AMN ∽ △ABC．

S_△EFN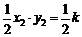＝．    ………………6分

∴S_△EFM ＝S_{△EF N}．            ………………­­­­­ 7分

由（1）中的结论可知：MN∥EF．  ………8分

② MN∥EF．          …………………10分

（若学生使用其他方法，只要解法正确，皆给分．）

∴ S_△EFM＝，    ………………5分

∴ ，．  

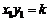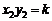∵ ME⊥y轴，NF⊥x轴， 

∴ OE＝y₁，OF＝x₂．

∵ 点M，N在反比例函数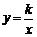（k＞0）的图象上，

23．(本题满分10分)

（1）证明：分别过点C，D，作CG⊥AB，DH⊥AB，

垂足为G，H，则∠CGA＝∠DHB＝90°．……1分

∴ CG∥DH．   

∵ △ABC与△ABD的面积相等， 

∴ CG＝DH．     …………………………2分

∴ 四边形CGHD为平行四边形． 

∴ AB∥CD．   ……………………………3分

（2）①证明：连结MF，NE．  …………………4分

设点M的坐标为（x₁，y₁），点N的坐标为（x₂，y₂）．

  即C，D之间的距离为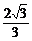km． ………………………………………………10分