
2.
已知复数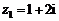 ,
,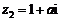 (
(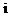 是虚数单位),若
是虚数单位),若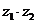 为纯虚数,则实数
为纯虚数,则实数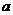 =_________.
=_________.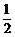
1.
集合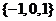 的所有子集个数为_________.8
的所有子集个数为_________.8
23. (本小题满分10分)
袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为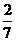 .现在甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,……,取后不放回,直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的,用
.现在甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,……,取后不放回,直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的,用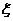 表示取球终止时所需要的取球次数.
表示取球终止时所需要的取球次数.
(Ⅰ)求袋中原有白球的个数;
(Ⅱ)求随机变量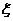 的概率分布及数学期望
的概率分布及数学期望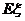 ;
;
(Ⅲ)求甲取到白球的概率.
22. (本小题满分10分)
(本小题满分10分)
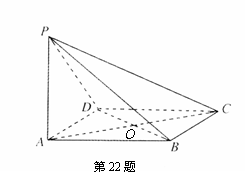
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.
(Ⅰ)求点A到平面PBD的距离;
(Ⅱ)求二面角A-PB-D的余弦值.
21.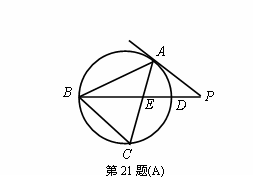 [选做题] 在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题] 在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
A.(选修4-1:几何证明选讲)
如图,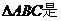 ⊙
⊙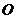 的内接三角形,
的内接三角形,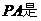 ⊙
⊙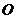 的切线,
的切线,
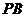 交
交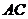 于点
于点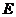 ,交⊙
,交⊙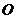 于点
于点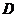 ,若
,若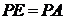 ,
,
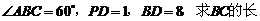 .
.
B.(选修4-2:矩阵与变换)
二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).
(Ⅰ)求矩阵M的逆矩阵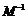 ;
;
(Ⅱ)设直线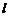 在变换M作用下得到了直线m:2x-y=4,求
在变换M作用下得到了直线m:2x-y=4,求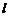 的方程.
的方程.
C.(选修4-4:坐标系与参数方程)
在极坐标系中,设圆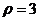 上的点到直线
上的点到直线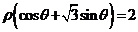 的距离为
的距离为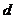 ,求
,求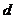 的最大值.
的最大值.
D.(选修4-5:不等式选讲)
设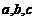 为正数且
为正数且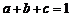 ,求证:
,求证: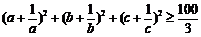 .
.
[必做题] 第22、23题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
20. (本小题满分16分)
在正项数列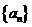 中,令
中,令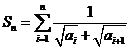 .
.
(Ⅰ)若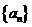 是首项为25,公差为2的等差数列,求
是首项为25,公差为2的等差数列,求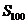 ;
;
(Ⅱ)若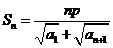 (
(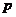 为正常数)对正整数
为正常数)对正整数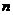 恒成立,求证
恒成立,求证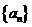 为等差数列;
为等差数列;
(Ⅲ)给定正整数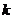 ,正实数
,正实数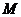 ,对于满足
,对于满足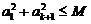 的所有等差数列
的所有等差数列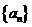 ,
,
求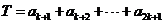 的最大值.
的最大值.
盐城市2008/2009高三第一次调研考试
数学附加题
(总分40分,考试时间30分钟)
19. (本小题满分16分)
已知函数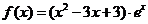 定义域为
定义域为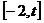 (
(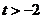 ),设
),设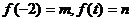 .
.
(Ⅰ)试确定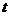 的取值范围,使得函数
的取值范围,使得函数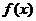 在
在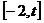 上为单调函数;
上为单调函数;
(Ⅱ)求证: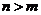 ;
;
(Ⅲ)求证:对于任意的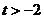 ,总存在
,总存在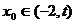 ,满足
,满足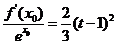 ,并确定这样的
,并确定这样的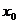 的个数.
的个数.
18. (本小题满分15分)
已知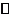
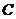 过点
过点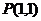 ,且与
,且与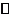
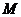 :
: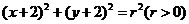 关于直线
关于直线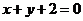 对称.
对称.
(Ⅰ)求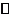
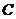 的方程;
的方程;
(Ⅱ)设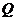 为
为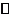
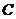 上的一个动点,求
上的一个动点,求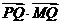 的最小值;
的最小值;
(Ⅲ)过点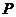 作两条相异直线分别与
作两条相异直线分别与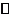
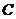 相交于
相交于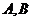 ,且直线
,且直线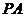 和直线
和直线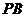 的倾斜角互补,
的倾斜角互补,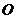 为坐标原点,试判断直线
为坐标原点,试判断直线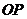 和
和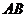 是否平行?请说明理由.
是否平行?请说明理由.
17. (本小题满分15分)
 如图,某小区准备在一直角围墙
如图,某小区准备在一直角围墙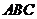 内的空地上植造一块“绿地
内的空地上植造一块“绿地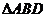 ”,其中
”,其中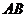 长为定值
长为定值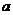 ,
,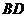 长可根据需要进行调节(
长可根据需要进行调节(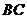 足够长).现规划在
足够长).现规划在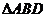 的内接正方形
的内接正方形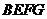 内种花,其余地方种草,且把种草的面积
内种花,其余地方种草,且把种草的面积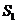 与种花的面积
与种花的面积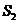 的比值
的比值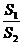 称为“草花比
称为“草花比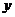 ”.
”.
(Ⅰ)设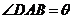 ,将
,将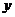 表示成
表示成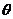 的函数关系式;
的函数关系式;
(Ⅱ)当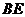 为多长时,
为多长时,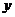 有最小值?最小值是多少?
有最小值?最小值是多少?
16.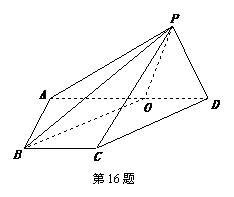 (本小题满分14分)
(本小题满分14分)
如图,在四棱锥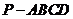 中,侧面
中,侧面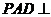 底面
底面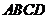 ,侧棱
,侧棱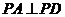 ,底面
,底面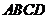 是直角梯形,其中
是直角梯形,其中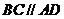 ,
,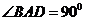 ,
,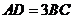 ,
,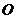 是
是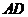 上一点.
上一点.
(Ⅰ)若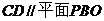 ,试指出点
,试指出点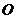 的位置;
的位置;
(Ⅱ)求证: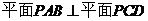 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com