
1.(2008海南、宁夏理)如图,已知点P在正方体ABCD-A1B1C1D1的对角线BD1上,∠PDA=60°。
 (1)求DP与CC1所成角的大小;(2)求DP与平面AA1D1D所成角的大小。
(1)求DP与CC1所成角的大小;(2)求DP与平面AA1D1D所成角的大小。
22.解:(Ⅰ)直角梯形ABCD的面积是
M底面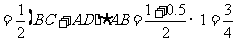 ,
,
∴ 四棱锥S-ABCD的体积是

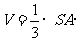 M底面
M底面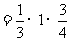
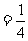 .
.
(Ⅱ)延长BA、CD相交于点E,连结SE,则SE是所求二面角的棱.
∵ AD∥BC,BC = 2AD,
∴ EA = AB = SA,∴ SE⊥SB,
∵ SA⊥面ABCD,得面SEB⊥面EBC,EB是交线,
又BC⊥EB,∴ BC⊥面SEB,故SB是CS在面SEB上的射影,∴ CS⊥SE,
所以∠BSC是所求二面角的平面角.
∵ 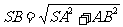
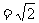 ,BC =1,BC⊥SB,
,BC =1,BC⊥SB,
∴ tg∠BSC 
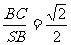 .
.
即所求二面角的正切值为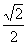 .
.
21、解:(1)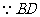 是圆的直径,∴
是圆的直径,∴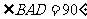 , 又
, 又 ∽
∽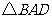 ,
,
∴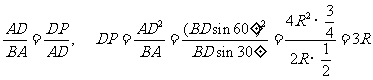 .
.
(2)在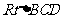 中,
中,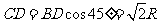 .
.
∵ ∴
∴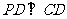
 又
又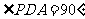 ,即
,即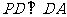 ,而
,而
∴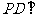 底面
底面

故三棱锥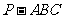 的体积为
的体积为
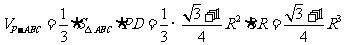 .
.
20.解:(1)已知EF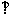 AB,那么翻折后,显然有PE
AB,那么翻折后,显然有PE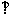 EF,又PE
EF,又PE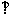 AE,从而PE
AE,从而PE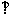 面ABC,即PE为四棱锥的高。
面ABC,即PE为四棱锥的高。
 四棱锥的底面积
四棱锥的底面积 而△BEF与△BDC相似,那么
而△BEF与△BDC相似,那么
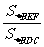 =
=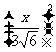 ,
,
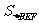 =
=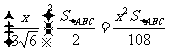
则 =
=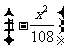
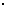
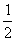
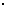 6
6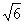
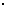 3=9
3=9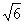
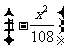
故四棱锥的体积V(x)=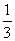 Sh=
Sh=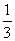
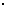 9
9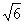
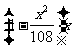 =
= 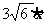
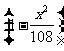 (0<x<3
(0<x<3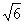 )
)
(2) V’(x)= 3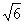 -
- x2(0<x<3
x2(0<x<3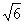 ), 令V’(x)=0得x=6
), 令V’(x)=0得x=6
当x∈(0,6)时,V’(x)>0,V(x)单调递增;x∈(6,3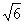 )时V’(x)><0,V(x)单调递减;
)时V’(x)><0,V(x)单调递减;
因此x=6时, V(x)取得最大值V(x)max=
V(6)=12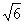
(3)过F作AC的平行线交AE于点G,连结FG、PG,则EG=6,EF=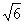 ,GF=PF=
,GF=PF= ,PG=
,PG= ,
,
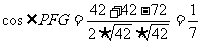
19.解:(Ⅰ)如图------ 3分
(Ⅱ)所求多面体体积
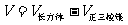
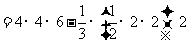
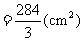 .------------------------7分
.------------------------7分
 (Ⅲ)证明:在长方体
(Ⅲ)证明:在长方体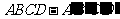 中,
中,
连结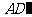 ,则
,则 .
.
因为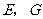 分别为
分别为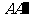 ,
, 中点,
中点,
所以 ,
,
从而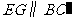 .又
.又 平面
平面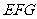 ,
,
所以 面
面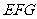 .--------------------12分
.--------------------12分
13. . 14 24 . 15.
. 14 24 . 15.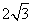 16. 30O . 17. 10 .
18.
16. 30O . 17. 10 .
18. ,
, 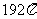 .
.
22. (2001江西、山西、天津文、理,广东,全国文、理)如图,在底面是直角梯形的四棱锥S-ABCD中,
(2001江西、山西、天津文、理,广东,全国文、理)如图,在底面是直角梯形的四棱锥S-ABCD中,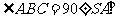 面ABCD,SA=AB=BC=1,AD=
面ABCD,SA=AB=BC=1,AD=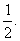
(Ⅰ)求四棱锥S-ABCD的体积;
(Ⅱ)求面SCD与面SBA所成的二面角的正切值.
历届高考中的“空间几何体”试题精选
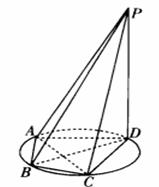
21.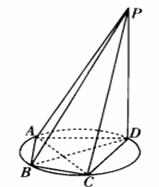 (2008广东文)如图5 所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径, ∠ABD=60o,∠BDC=45o.△ADP∽△BAD.
(2008广东文)如图5 所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径, ∠ABD=60o,∠BDC=45o.△ADP∽△BAD.
(1)求线段PD的长; (2)若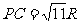 ,求三棱锥P-ABC的体积.
,求三棱锥P-ABC的体积.
20. (2007广东理)如图所示,等腰△ABC的底边AB=6
(2007广东理)如图所示,等腰△ABC的底边AB=6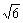 ,高CD=3,点B是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记BE=x,V(x)表示四棱锥P-ACFE的体积.
,高CD=3,点B是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记BE=x,V(x)表示四棱锥P-ACFE的体积.
(1)求V(x)的表达式; (2)当x为何值时,V(x)取得最大值?
(3)当V(x)取得最大值时,求异面直线AC与PF所成角的余弦值
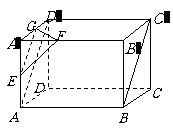
19. (2008海南、宁夏文)如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm)。
(2008海南、宁夏文)如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm)。
(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(2)按照给出的尺寸,求该多面体的体积;
(3)在所给直观图中连结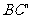 ,证明:
,证明: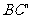 ∥面EFG。
∥面EFG。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com