
2.已知向量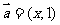 ,
,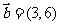 ,且
,且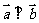 ,则实数
,则实数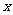 的值为( )
的值为( )
A.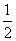 B.
B.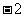 C.
C.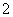 D.
D.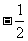
1.若集合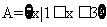 ,
,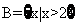 ,则
,则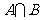 等于( )
等于( )
A.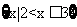 B.
B.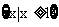 C.
C.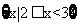 D.
D.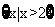
3. 3.用 x,
x, y,
y, z,
z, (x+y),
(x+y), (x-y)表示下列各式:
(x-y)表示下列各式:
(1) 
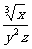 ;
(2)
;
(2) (
(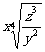 );
);
(3)  (
(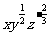 ); (4)
); (4)
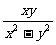 ;
;
(5) (
(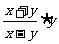 ); (6)
); (6) [
[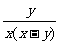 ]3.
]3.
解:(1) 
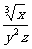 =
=
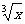 -
-
 z
z
=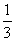
 x-(2
x-(2 y+
y+ z)
z)
=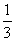
 x-2
x-2 y-
y- z;
z;
(2)  (x·
(x·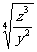 )=
)= x+
x+
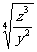
= x+
x+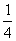 (
(
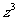 -
-
 )
)
= x-
x-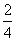
 y+
y+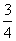
 z
z
= x-
x- y+
y+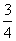
 z;
z;
(3)  (x
(x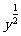
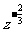 )=
)= x+
x+
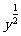 +
+
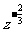 ?
?
= x+
x+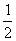
 y-
y-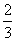
 z;
z;
(4) 
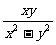 =
= xy-
xy- (
(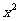 -
- )
)
= x+
x+ y-
y- (x+y)(x-y)
(x+y)(x-y)
= x+
x+ y-
y- (x+y)-
(x+y)- (x-y);
(x-y);
(5)  (
(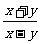 ·y)=
·y)=
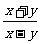 +
+ y
y
= (x+y)-
(x+y)- (x-y)+
(x-y)+ y;
y;
(6)  [
[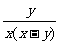 ]
]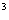
=3[ y-
y- x-
x- (x-y)]
(x-y)]
=3 y-3
y-3 x-3
x-3 (x-y)
(x-y)
2.已知lg2=0.3010,lg3=0.4771,求下列各对数的值(精确到小数点后第四位)
(1) lg6 (2)lg4 (3)lg12
(4)lg 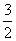 (5)lg
(5)lg 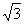 (6)lg32
(6)lg32
解:(1)lg6=lg2+lg3=0.3010+0.4771=0.7781
(2) lg4=2lg2=2×0.3010=0.6020
(3) lg12=lg(3×4)=lg3+2lg2=0.4771+0.3010×2=1.0791
(4) lg 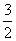 =lg3-lg2=0.4771-0.3010=0.1761
=lg3-lg2=0.4771-0.3010=0.1761
(5) lg 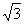 =
=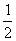 lg3=
lg3=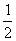 ×0.4771=0.2386
×0.4771=0.2386
(6) lg32=5lg2=5×0.3010=1.5050
1.计算:
(1)  2+
2+
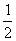 (a>0,a≠1) (2)
(a>0,a≠1) (2) 18-
18- 2
2
(3) lg 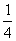 -lg25
(4)2
-lg25
(4)2 10+
10+ 0.25
0.25
(5)2 25+3
25+3 64
(6)
64
(6)  (
( 16)
16)
解:(1)  2+
2+
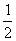 =
= (2×
(2×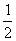 )=
)= 1=0
1=0
(2)  18-
18- 2=
2=
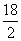 =
= 9=2
9=2
(3)lg 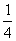 -lg25=lg(
-lg25=lg(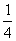 ÷25)=lg
÷25)=lg 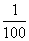 =lg
=lg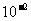 =-2
=-2
(4)2 10+
10+ 0.25=
0.25=
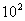 +
+ 0.25
0.25
= (100×0.25)=
(100×0.25)= 25=2
25=2
(5)2 25+3
25+3 64=2
64=2
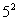 +3
+3
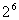
=2×2+3×6=22
(6)  (
( 16)=
16)= (
(
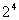 )=
)= 4=
4=
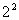 =2
=2
2. 用lgx,lgy,lgz表示下列各式:
(1) lg(xyz); (2)lg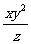 ; (3)
; (3)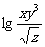 ; (4)
; (4)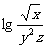
解:(1) lg(xyz)=lgx+lgy+lgz;
(2) lg 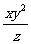 =lgx
=lgx -lgz=lgx+lg
-lgz=lgx+lg -lgz
-lgz
=lgx+2lgy-lgz;
(3) 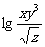 =lgx
=lgx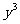 -lg
-lg 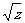 =lgx+lg
=lgx+lg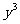 -
-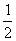 lgz
lgz
=lgx+3lgy-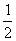 lgz;
lgz;
(4)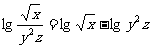
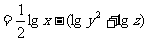

1.求下列各式的值:
(1) 6-
6- 3
3 (2)lg5+lg2
(2)lg5+lg2
(3) 3+
3+
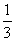
 (4)
(4) 5-
5- 15
15
解:(1) 6-
6- 3=
3=
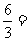
 2=1
2=1
(2)lg5+lg2=lg(5×2)=lg10=1
(3)  3+
3+
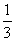 =
= (3×
(3×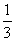 )=
)= 1=0
1=0
(4)  5-
5- 15=
15=
 =
=
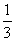 =-
=- 3=-1.
3=-1.
例1 计算
(1) 25, (2)
25, (2)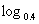 1, (3)
1, (3) (
(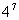 ×
×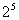 ), (4)lg
), (4)lg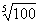
解:(1) 25=
25= 
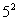 =2
=2
(2)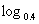 1=0
1=0
(3) (
(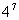 ×25)=
×25)= 
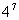 +
+ 
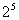
= 
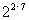 +
+ 
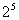 = 2×7+5=19
= 2×7+5=19
(4)lg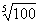 =
=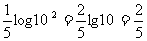

例2 用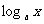 ,
,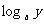 ,
,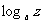 表示下列各式:
表示下列各式:


解:(1) =
= (xy)-
(xy)- z=
z= x+
x+ y-
y-  z
z
(2)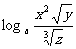 =
= (
(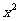
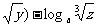
= 
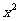 +
+
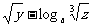 =2
=2 x+
x+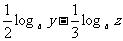

例3计算:
(1)lg14-2lg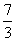 +lg7-lg18
(2)
+lg7-lg18
(2)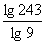 (3)
(3)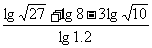
说明:此例题可讲练结合.
(1)解法一:lg14-2lg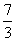 +lg7-lg18
+lg7-lg18
=lg(2×7)-2(lg7-lg3)+lg7-lg(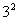 ×2)
×2)
=lg2+lg7-2lg7+2lg3+lg7-2lg3-lg2=0 ?
?
解法二:
lg14-2lg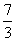 +lg7-lg18=lg14-lg
+lg7-lg18=lg14-lg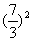 +lg7-lg18?
+lg7-lg18?
=lg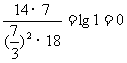

评述:此题体现了对数运算性质的灵活运用,运算性质的逆用常被学生所忽视.
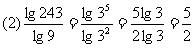

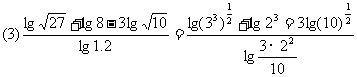

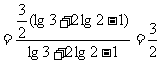

评述:此例题体现对数运算性质的综合运用,应注意掌握变形技巧,如(3)题各部分变形要化到最简形式,同时注意分子、分母的联系.(2)题要避免错用对数运算性质.
积、商、幂的对数运算法则:
如果 a > 0,a ¹ 1,M > 0, N > 0 有:
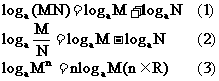
证明:①设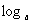 M=p,
M=p,  N=q
N=q
由对数的定义可以得:M=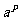 ,N=
,N=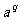

∴MN= 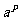
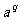 =
=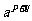 ∴
∴ MN=p+q,
MN=p+q,
即证得 MN=
MN= M +
M +  N
N
②设 M=p,
M=p, N=q
N=q
由对数的定义可以得M=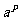 ,N=
,N=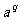

∴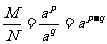 ∴
∴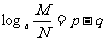

即证得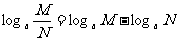

③设 M=P 由对数定义可以得M=
M=P 由对数定义可以得M=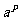 ,
,
∴ =
=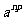 ∴
∴
 =np, 即证得
=np, 即证得
 =n
=n M
M
说明:上述证明是运用转化的思想,先通过假设,将对数式化成指数式,并利用幂的运算性质进行恒等变形;然后再根据对数定义将指数式化成对数式
①简易语言表达:“积的对数 = 对数的和”……
②有时逆向运用公式:如

③真数的取值范围必须是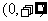 :
:
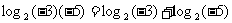 是不成立的
是不成立的
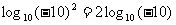 是不成立的
是不成立的
④对公式容易错误记忆,要特别注意:
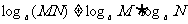 ,
,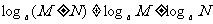

3.指数运算法则 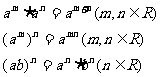

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com