
3.概念辨析:为使大家巩固倾斜角和斜率的概念,我们来看下面的题.
关于直线的倾斜角和斜率,下列哪些说法是正确的:
A.任一条直线都有倾斜角,也都有斜率;
B.直线的倾斜角越大,它的斜率就越大;
C.平行于 轴的直线的倾斜角是0或π;
轴的直线的倾斜角是0或π;
D.两直线的倾斜角相等,它们的斜率也相等.
E.直线斜率的范围是(-∞,+∞).
辨析:上述说法中,E正确,其余均错误,原因是:A.与x轴垂直的直线倾斜角为 ,但斜率不存在;B.举反例说明,120°>30°,但
,但斜率不存在;B.举反例说明,120°>30°,但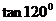 =-
=-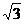 <
<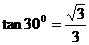 ;C.平行于
;C.平行于 轴的直线的倾斜角为0;D.如果两直线的倾斜角都是
轴的直线的倾斜角为0;D.如果两直线的倾斜角都是 ,但斜率不存在,也就谈不上相等.
,但斜率不存在,也就谈不上相等.
说明:①当直线和 轴平行或重合时,我们规定直线的倾斜角为0°;②直线倾斜角的取值范围是
轴平行或重合时,我们规定直线的倾斜角为0°;②直线倾斜角的取值范围是 ;③倾斜角是90°的直线没有斜率.
;③倾斜角是90°的直线没有斜率.
2.直线的倾斜角与斜率:在平面直角坐标系中,对于一条与 轴相交的直线,如果把
轴相交的直线,如果把 轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记为
轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记为 ,那么
,那么 就叫做直线的倾斜角.
就叫做直线的倾斜角.
当直线和 轴平行或重合时,我们规定直线的倾斜角为0°
轴平行或重合时,我们规定直线的倾斜角为0° 因此,根据定义,我们可以得到倾斜角的取值范围是0°≤
因此,根据定义,我们可以得到倾斜角的取值范围是0°≤ <180°
<180°
倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率,常用 表示. 倾斜角是
表示. 倾斜角是 的直线没有斜率
的直线没有斜率
1.直线方程的概念:以一个方程的解为坐标的点都是某条直线上的点,反过来,这条直线上的点的坐标都是这个方程的解,这时,这个方程就叫做这条直线的方程,这条直线叫做这个方程的直线
在平面直角坐标系中研究直线时,就是利用直线与方程的这种关系,建立直线的方程的概念,并通过方程来研究直线的有关问题.为此,我们先研究直线的倾斜角和斜率
3.这两点与函数式的关系:这两点就是满足函数式的两对 值.
值.
因此,我们可以得到这样一个结论:一般地,一次函数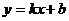 的图象是一条直线,它是以满足
的图象是一条直线,它是以满足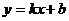 的每一对
的每一对 的值为坐标的点构成的.
的值为坐标的点构成的.
由于函数式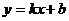 也可以看作二元一次方程.所以我们可以说,这个方程的解和直线上的点也存在这样的对应关系.
也可以看作二元一次方程.所以我们可以说,这个方程的解和直线上的点也存在这样的对应关系.
有了上述基础,我们也就不难理解“直线的方程”和“方程的直线”的基本概念
2.对于一给定函数 ,作出它的图象的方法:由于两点确定一条直线,所以在直线上任找两点即可.
,作出它的图象的方法:由于两点确定一条直线,所以在直线上任找两点即可.
在初中,我们已经学习过一次函数,并接触过一次函数的图象,现在,请同学们作一下回顾:
1.一次函数的图象特点:一次函数形如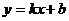 ,它的图象是一条直线.
,它的图象是一条直线.
1 若cosx=0,则角x等于( )
若cosx=0,则角x等于( )
A.kπ,(k∈Z)
B.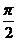 +kπ,(k∈Z)
+kπ,(k∈Z)
C.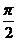 +2kπ,(k∈Z) D.-
+2kπ,(k∈Z) D.-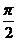 +2kπ,(k∈Z)
+2kπ,(k∈Z)
2 若tanx=0,则角x等于( )
若tanx=0,则角x等于( )
A.kπ,(k∈Z)
B.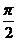 +kπ,(k∈Z)
+kπ,(k∈Z)
C.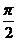 +2kπ,(k∈Z) D.-
+2kπ,(k∈Z) D.-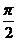 +2kπ,(k∈Z)
+2kπ,(k∈Z)
3 已知cosx=-
已知cosx=-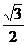 ,π<x<2π,则x等于( )
,π<x<2π,则x等于( )
A.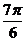 B.
B.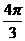 C.
C. D.
D.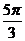
4 若tan(3π-x)=-
若tan(3π-x)=-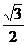 ,则x=
,则x=

5 满足tanx=
满足tanx= 的x的集合为
的x的集合为 
6 在闭区间[0,2π]上,适合关系式cosx=-0.4099的角有 个,用0.4099的反余弦表示的x值是
___________;用-0
在闭区间[0,2π]上,适合关系式cosx=-0.4099的角有 个,用0.4099的反余弦表示的x值是
___________;用-0 4099的反余弦表示的x的值是
_________
4099的反余弦表示的x的值是
_________
例1
(1)已知 ,求x(精确到
,求x(精确到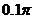 )
)
解:在区间 上
上 是增函数,符合条件的角是唯一的
是增函数,符合条件的角是唯一的

(2)已知 且
且 ,求x的取值集合
,求x的取值集合
解: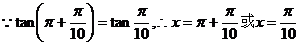
 所求的x的集合是
所求的x的集合是 (即
(即 )
)
(3)已知 ,求x的取值集合
,求x的取值集合
解:由上题可知: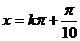 ,
,
合并为
例2已知 ,根据所给范围求
,根据所给范围求 :
:
1° 为锐角 2°
为锐角 2° 为某三角形内角 3°
为某三角形内角 3° 为第二象限角 4°
为第二象限角 4°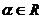
解:1°由题设
2°设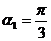 ,或
,或
3°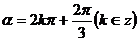
4°由题设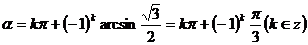
例3 求适合下列关系的x的集合
1°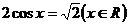 2°
2° 3°
3°
解:1°
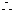 所求集合为
所求集合为
2° 所求集合为
所求集合为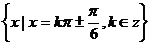
3°
例4 直角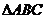 锐角A,B满足:
锐角A,B满足: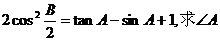
解:由已知:
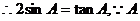 为锐角,
为锐角,
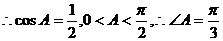
例5 1°用反三角函数表示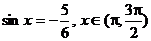 中的角x
中的角x
2°用反三角函数表示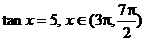 中的角x
中的角x
解:1° ∵ ∴
∴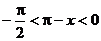
又由 得
得
∴ ∴
∴
2° ∵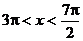 ∴
∴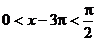
又由 得
得
∴ ∴
∴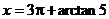
例6已知 ,求角x的集合
,求角x的集合
解:∵ ∴
∴
由 得
得 
由 得
得 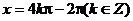
故角x的集合为
例7求 的值
的值
解:arctan2 = a, arctan3 = b 则tana = 2, tanb = 3
且 ,
, 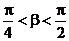
∴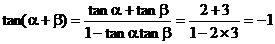
而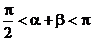 ∴a + b =
∴a + b = 
又arctan1
=  ∴
∴ = p
= p
例8求y = arccos(sinx), ( )的值域
)的值域
解:设u = sin x ∵ ∴
∴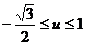
∴ ∴所求函数的值域为
∴所求函数的值域为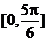
反正切函数

1°在整个定义域上无反函数
2°在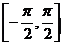 上
上 的反函数称作反正切函数,
的反函数称作反正切函数,
记作 (奇函数)
(奇函数)
2.已知三角函数求角:
求角的多值性法则:1、先决定角的象限 2、如果函数值是正值,则先求出对应的锐角x; 如果函数值是负值,则先求出与其绝对值对应的锐角x,3、由诱导公式,求出符合条件的其它象限的角
2、如果函数值是正值,则先求出对应的锐角x; 如果函数值是负值,则先求出与其绝对值对应的锐角x,3、由诱导公式,求出符合条件的其它象限的角
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com