
3.对于具有周期性的函数,应先求出周期,作图象时只要作出一个周期的图象,就可根据周期性作出整个函数的图象。
2.作函数的图象时,首先要确定函数的定义域.
1.数形结合是数学中重要的思想方法,在中学阶段,对各类函数的研究都离不开图象,很多函数的性质都是通过观察图象而得到的.
题型1:三角函数的图象
例1.(2009浙江理)已知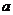 是实数,则函数
是实数,则函数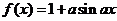 的图象不可能是 ( )
的图象不可能是 ( )


解析 对于振幅大于1时,三角函数的周期为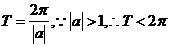 ,而D不符合要求,它的振幅大于1,但周期反而大于了
,而D不符合要求,它的振幅大于1,但周期反而大于了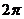 .
.
答案:D 

例2.(2009辽宁理,8)已知函数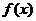 =Acos(
=Acos(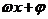 )的图象如图所示,
)的图象如图所示, ,则
,则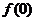 =( )
=( )

A.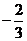 B.
B. 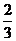 C.-
C.- 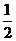 D.
D.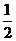

答案 C
题型2:三角函数图象的变换
例3.试述如何由y=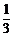 sin(2x+
sin(2x+ )的图象得到y=sinx的图象.
)的图象得到y=sinx的图象.
解析:y=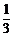 sin(2x+
sin(2x+ )
)
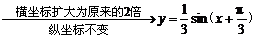





另法答案:
(1)先将y=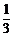 sin(2x+
sin(2x+ )的图象向右平移
)的图象向右平移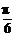 个单位,得y=
个单位,得y=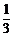 sin2x的图象;
sin2x的图象;
(2)再将y=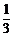 sin2x上各点的横坐标扩大为原来的2倍(纵坐标不变),得y=
sin2x上各点的横坐标扩大为原来的2倍(纵坐标不变),得y=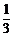 sinx的图象;
sinx的图象;
(3)再将y=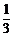 sinx图象上各点的纵坐标扩大为原来的3倍(横坐标不变),即可得到y=sinx的图象。
sinx图象上各点的纵坐标扩大为原来的3倍(横坐标不变),即可得到y=sinx的图象。
例4.(2009山东卷理)将函数 的图象向左平移
的图象向左平移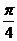 个单位, 再向上平移1个单位,所得图象的函数解析式是(
).
个单位, 再向上平移1个单位,所得图象的函数解析式是(
).
A.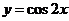 B.
B.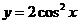 C.
C. D.
D.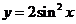

解析 将函数 的图象向左平移
的图象向左平移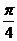 个单位,得到函数
个单位,得到函数 即
即 的图象,再向上平移1个单位,所得图象的函数解析式为
的图象,再向上平移1个单位,所得图象的函数解析式为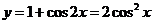 ,故选B.
,故选B.
答案:B
[命题立意]:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式的基本知识和基本技能,学会公式的变形.

7.(2009山东卷文)将函数 的图象向左平移
的图象向左平移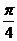 个单位, 再向上平移1个单位,所得图象的函数解析式是(
).
个单位, 再向上平移1个单位,所得图象的函数解析式是(
).
A. 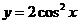 B.
B. 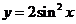 C.
C. D.
D. 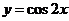

解析 将函数 的图象向左平移
的图象向左平移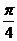 个单位,得到函数
个单位,得到函数 即
即 的图象,再向上平移1个单位,所得图象的函数解析式为
的图象,再向上平移1个单位,所得图象的函数解析式为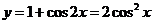 ,故选A.
,故选A.
答案:A
[命题立意]:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式的基本知识和基本技能,学会公式的变形.

题型3:三角函数图象的应用
例5.已知电流I与时间t的关系式为 。
。
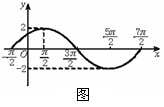
(1)右图是 (ω>0,
(ω>0, )
)
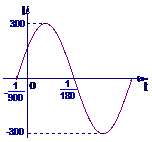 在一个周期内的图象,根据图中数据求
在一个周期内的图象,根据图中数据求

的解析式;
(2)如果t在任意一段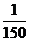 秒的时间内,电流
秒的时间内,电流 都能取得最大值和最小值,那么ω的最小正整数值是多少?
都能取得最大值和最小值,那么ω的最小正整数值是多少?
解析:本小题主要考查三角函数的图象与性质等基础知识,考查运算能力和逻辑推理能力.
(1)由图可知 A=300。
设t1=-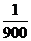 ,t2=
,t2=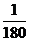 ,
, 
则周期T=2(t2-t1)=2(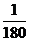 +
+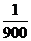 )=
)= 。
。
∴ ω=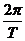 =150π。
=150π。
又当t=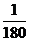 时,I=0,即sin(150π·
时,I=0,即sin(150π·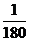 +
+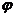 )=0,
)=0,
而 , ∴
, ∴ 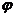 =
=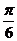 。
。
故所求的解析式为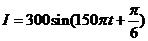 。
。
(2)依题意,周期T≤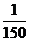 ,即
,即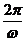 ≤
≤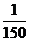 ,(ω>0)
,(ω>0)
∴ ω≥300π>942,又ω∈N*,
故最小正整数ω=943。
 点评:本题解答的开窍点是将图形语言转化为符号语言.其中,读图、识图、用图是形数结合的有效途径.
点评:本题解答的开窍点是将图形语言转化为符号语言.其中,读图、识图、用图是形数结合的有效途径.
例6.(1)(2009辽宁卷理)已知函数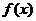 =Acos(
=Acos(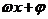 )的图象如图所示,
)的图象如图所示, ,则
,则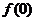 =( )
=( )
A.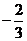 B.
B. 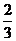 C.-
C.- 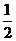 D.
D.
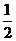

解析 由图象可得最小正周期为
于是f(0)=f(),注意到与关于对称
所以f()=-f()=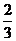
答案 B
(2)(2009宁夏海南卷理)已知函数y=sin( x+
x+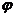 )(
)( >0, -
>0, -
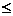
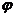 <
< )的图像如图所示,则
)的图像如图所示,则 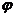 =________________
=________________

解析:由图可知,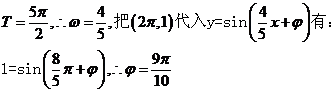
答案: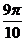
题型4:三角函数的定义域、值域
例7.(1)已知f(x)的定义域为[0,1],求f(cosx)的定义域;
(2)求函数y=lgsin(cosx)的定义域;
分析:求函数的定义域:(1)要使0≤cosx≤1,(2)要使sin(cosx)>0,这里的cosx以它的值充当角。
解析:(1)0≤cosx<1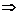 2kπ-
2kπ-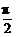 ≤x≤2kπ+
≤x≤2kπ+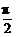 ,且x≠2kπ(k∈Z)。
,且x≠2kπ(k∈Z)。
∴所求函数的定义域为{x|x∈[2kπ-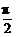 ,2kπ+
,2kπ+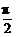 ]且x≠2kπ,k∈Z}。
]且x≠2kπ,k∈Z}。
(2)由sin(cosx)>0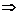 2kπ<cosx<2kπ+π(k∈Z)。
2kπ<cosx<2kπ+π(k∈Z)。
又∵-1≤cosx≤1,∴0<cosx≤1。
故所求定义域为{x|x∈(2kπ-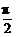 ,2kπ+
,2kπ+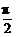 ),k∈Z}。
),k∈Z}。
点评:求三角函数的定义域,要解三角不等式,常用的方法有二:一是图象,二是三角函数线.
例8.已知函数f(x)= ,求f(x)的定义域,判断它的奇偶性,并求其值域.
,求f(x)的定义域,判断它的奇偶性,并求其值域.
解析:由cos2x≠0得2x≠kπ+ ,解得x≠
,解得x≠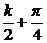 ,k∈Z,所以f(x)的定义域为{x|x∈R且x≠
,k∈Z,所以f(x)的定义域为{x|x∈R且x≠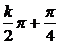 ,k∈Z},
,k∈Z},
因为f(x)的定义域关于原点对称,
且f(-x)=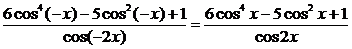 =f(x)。
=f(x)。
所以f(x)是偶函数。
又当x≠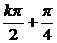 (k∈Z)时,
(k∈Z)时,
f(x)=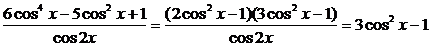 。
。
所以f(x)的值域为{y|-1≤y< 或
或 <y≤2}。
<y≤2}。
点评:本题主要考查三角函数的基本知识,考查逻辑思维能力、分析和解决问题的能力。
题型5:三角函数的单调性
例9.求下列函数的单调区间:
(1)y= sin(
sin( -
- );(2)y=-|sin(x+
);(2)y=-|sin(x+ )|。
)|。
分析:(1)要将原函数化为y=- sin(
sin(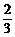 x-
x- )再求之。
)再求之。
(2)可画出y=-|sin(x+ )|的图象.
)|的图象.
解:(1)y= sin(
sin( -
- )=-
)=- sin(
sin( -
- )。
)。
故由2kπ-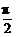 ≤
≤ -
- ≤2kπ+
≤2kπ+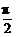 。
。
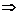 3kπ-
3kπ- ≤x≤3kπ+
≤x≤3kπ+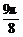 (k∈Z),为单调减区间;
(k∈Z),为单调减区间;
由2kπ+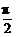 ≤
≤ -
- ≤2kπ+
≤2kπ+ 。
。
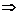 3kπ+
3kπ+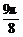 ≤x≤3kπ+
≤x≤3kπ+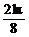 (k∈Z),为单调增区间。
(k∈Z),为单调增区间。
∴递减区间为[3kπ- ,3kπ+
,3kπ+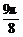 ],
],
递增区间为[3kπ+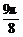 ,3kπ+
,3kπ+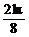 ](k∈Z)。
](k∈Z)。
(2)y=-|sin(x+ )|的图象的增区间为[kπ+
)|的图象的增区间为[kπ+ ,kπ+
,kπ+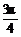 ],减区间为[kπ-
],减区间为[kπ- ,kπ+
,kπ+ ]。
]。
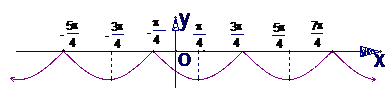
例10.(2002京皖春文,9)函数y=2sinx的单调增区间是( )
A.[2kπ- ,2kπ+
,2kπ+ ](k∈Z)
](k∈Z)
B.[2kπ+ ,2kπ+
,2kπ+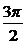 ](k∈Z)
](k∈Z)
C.[2kπ-π,2kπ](k∈Z)
D.[2kπ,2kπ+π](k∈Z)
解析:A;函数y=2x为增函数,因此求函数y=2sinx的单调增区间即求函数y=sinx的单调增区间.
题型6:三角函数的奇偶性
例11.判断下面函数的奇偶性:f(x)=lg(sinx+ )。
)。
分析:判断奇偶性首先应看定义域是否关于原点对称,然后再看f(x)与f(-x)的关系。
解析:定义域为R,又f(x)+f(-x)=lg1=0,
即f(-x)=-f(x),∴f(x)为奇函数。
点评:定义域关于原点对称是函数具有奇偶性的必要(但不充分)条件。
例12.(2001上海春)关于x的函数f(x)=sin(x+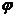 )有以下命题:
)有以下命题:
①对任意的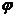 ,f(x)都是非奇非偶函数;
,f(x)都是非奇非偶函数;
②不存在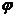 ,使f(x)既是奇函数,又是偶函数;
,使f(x)既是奇函数,又是偶函数;
③存在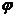 ,使f(x)是奇函数;
,使f(x)是奇函数;
④对任意的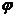 ,f(x)都不是偶函数。
,f(x)都不是偶函数。
其中一个假命题的序号是_____.因为当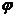 =_____时,该命题的结论不成立.
=_____时,该命题的结论不成立.
答案:①,kπ(k∈Z);或者①,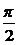 +kπ(k∈Z);或者④,
+kπ(k∈Z);或者④,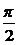 +kπ(k∈Z)
+kπ(k∈Z)
解析:当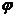 =2kπ,k∈Z时,f(x)=sinx是奇函数。当
=2kπ,k∈Z时,f(x)=sinx是奇函数。当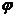 =2(k+1)π,k∈Z时f(x)=-sinx仍是奇函数。当
=2(k+1)π,k∈Z时f(x)=-sinx仍是奇函数。当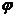 =2kπ+
=2kπ+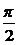 ,k∈Z时,f(x)=cosx,或当
,k∈Z时,f(x)=cosx,或当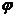 =2kπ-
=2kπ-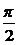 ,k∈Z时,f(x)=-cosx,f(x)都是偶函数.所以②和③都是正确的。无论
,k∈Z时,f(x)=-cosx,f(x)都是偶函数.所以②和③都是正确的。无论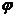 为何值都不能使f(x)恒等于零。所以f(x)不能既是奇函数又是偶函数。①和④都是假命题。
为何值都不能使f(x)恒等于零。所以f(x)不能既是奇函数又是偶函数。①和④都是假命题。
点评:本题考查三角函数的奇偶性、诱导公式以及分析问题的能力,注意k∈Z不能不写,否则不给分,本题的答案不惟一,两个空全答对才能得分.
题型7:三角函数的周期性
例13.求函数y=sin6x+cos6x的最小正周期,并求x为何值时,y有最大值。
分析:将原函数化成y=Asin(ωx+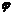 )+B的形式,即可求解.
)+B的形式,即可求解.
解析:y=sin6x+cos6x=(sin2x+cos2x)(sin4x-sin2xcos2x+cos4x)
=1-3sin2xcos2x=1- sin22x=
sin22x=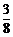 cos4x+
cos4x+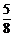 。
。
∴T=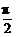 。
。
当cos4x=1,即x= (k∈Z)时,ymax=1。
(k∈Z)时,ymax=1。
例14.设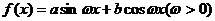 的周期
的周期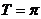 ,最大值
,最大值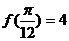 ,
,
(1)求 、
、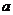 、
、 的值;
的值;
(2)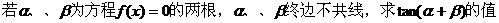 。
。
解析:(1) 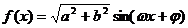 ,
,  ,
, 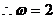 ,
,
又  的最大值。
的最大值。
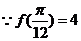 ,
, 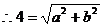 ① ,且
① ,且 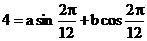 ②,
②,
由 ①、②解出 a=2 , b=3.
(2) 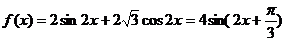 ,
, 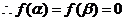 ,
,
 ,
,
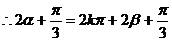 , 或
, 或 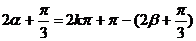 ,
,
即 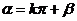 (
(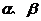 共线,故舍去) , 或
共线,故舍去) , 或  ,
,
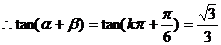
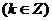 。
。
点评:方程组的思想是解题时常用的基本思想方法;在解题时不要忘记三角函数的周期性。
题型8:三角函数的最值
例15.(2009安徽卷文)设函数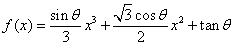 ,其中
,其中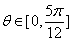 ,则导数
,则导数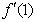 的取值范围是
的取值范围是
A.  B.
B. 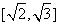 C.
C. D.
D. 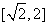
解析 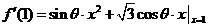
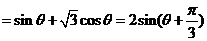
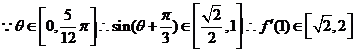 ,选D
,选D
例16.(2009江西卷理)若函数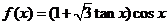 ,
,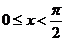 ,则
,则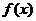 的最大值为
的最大值为
A.1
B.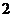 C.
C.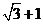 D.
D.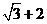
答案:B
解析 因为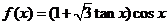 =
=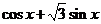 =
=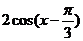
当 是,函数取得最大值为2. 故选B
是,函数取得最大值为2. 故选B
9.五点法作y=Asin(ωx+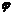 )的简图:
)的简图:
五点取法是设x=ωx+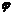 ,由x取0、
,由x取0、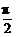 、π、
、π、 、2π来求相应的x值及对应的y值,再描点作图。
、2π来求相应的x值及对应的y值,再描点作图。
8.求三角函数的周期的常用方法:
经过恒等变形化成“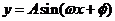 、
、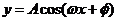 ”的形式,在利用周期公式,另外还有图像法和定义法.
”的形式,在利用周期公式,另外还有图像法和定义法.
7.求三角函数的单调区间:一般先将函数式化为基本三角函数的标准式,要特别注意A、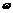 的正负.利用单调性三角函数大小一般要化为同名函数,并且在同一单调区间;
的正负.利用单调性三角函数大小一般要化为同名函数,并且在同一单调区间;
6.对称轴与对称中心:
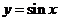 的对称轴为
的对称轴为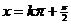 ,对称中心为
,对称中心为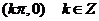 ;
;
 的对称轴为
的对称轴为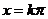 ,对称中心为
,对称中心为 ;
;
对于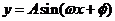 和
和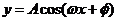 来说,对称中心与零点相联系,对称轴与最值点联系。
来说,对称中心与零点相联系,对称轴与最值点联系。
5.由y=Asin(ωx+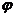 )的图象求其函数式:
)的图象求其函数式:
给出图象确定解析式y=Asin(ωx+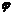 )的题型,有时从寻找“五点”中的第一零点(-
)的题型,有时从寻找“五点”中的第一零点(-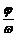 ,0)作为突破口,要从图象的升降情况找准第一个零点的位置。
,0)作为突破口,要从图象的升降情况找准第一个零点的位置。
4.由y=sinx的图象变换出y=sin(ωx+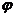 )的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换。
)的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换。
利用图象的变换作图象时,提倡先平移后伸缩,但先伸缩后平移也经常出现.无论哪种变形,请切记每一个变换总是对字母x而言,即图象变换要看“变量”起多大变化,而不是“角变化”多少。
途径一:先平移变换再周期变换(伸缩变换)
先将y=sinx的图象向左(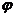 >0)或向右(
>0)或向右(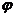 <0=平移|
<0=平移|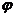 |个单位,再将图象上各点的横坐标变为原来的
|个单位,再将图象上各点的横坐标变为原来的 倍(ω>0),便得y=sin(ωx+
倍(ω>0),便得y=sin(ωx+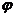 )的图象.
)的图象.
途径二:先周期变换(伸缩变换)再平移变换。
先将y=sinx的图象上各点的横坐标变为原来的 倍(ω>0),再沿x轴向左(
倍(ω>0),再沿x轴向左(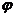 >0)或向右(
>0)或向右(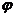 <0=平移
<0=平移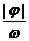 个单位,便得y=sin(ωx+
个单位,便得y=sin(ωx+ )的图象。
)的图象。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com