
设数列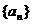 、
、 分别满足
分别满足 ,
, ,
, .
.
 (Ⅰ)求证:A1B∥平面AC1D;
(Ⅰ)求证:A1B∥平面AC1D;
(Ⅱ)求二面角C-AC1-D的大小.
(20)(本小题满分12分)
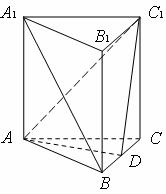 如图,在正三棱柱ABC-A1B1C1中,AB=AA1,D是BC上一点,且AD⊥C1D.
如图,在正三棱柱ABC-A1B1C1中,AB=AA1,D是BC上一点,且AD⊥C1D.
 有一种舞台灯,外形是正六棱柱,在其每一个侧面上安装5只颜色各异的彩灯,假若每只灯正常发光的概率为
有一种舞台灯,外形是正六棱柱,在其每一个侧面上安装5只颜色各异的彩灯,假若每只灯正常发光的概率为 . 若一个面上至少有3只灯发光,则不需要维修,否则需要更换这个面进行维修.
. 若一个面上至少有3只灯发光,则不需要维修,否则需要更换这个面进行维修.
(Ⅰ)求一个面需要维修的概率;
(Ⅱ)求至少有3个面需要维修的概率.
(19)(本小题满分12分)
(Ⅱ)设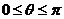 ,且函数
,且函数 为偶函数,求满足
为偶函数,求满足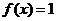 ,
,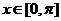 的x的集合.
的x的集合.
(18)(本小题满分12分)
(Ⅰ)求 的最小正周期;
的最小正周期;
 已知
已知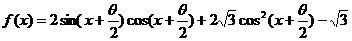 .
.
(16)已知定义域为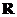 的函数
的函数 是奇函数,那么函数
是奇函数,那么函数 的反函数是___________________________.
的反函数是___________________________.
(17)(本小题满分10分)
(15)设正四棱锥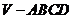 的底面ABCD在一个球的大圆上,顶点V也在这个球面上,那么它的侧面与底面所成的二面角为_______________.
的底面ABCD在一个球的大圆上,顶点V也在这个球面上,那么它的侧面与底面所成的二面角为_______________.
(14)设 ,式中变量
,式中变量 ,
, 满足
满足 ,则
,则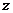 的最小值为_________.
的最小值为_________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com