设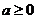，函数，.

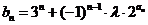（Ⅱ）设（），试确定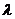的值，使得对任意，都有成立．

（22）（本小题满分12分）

（Ⅰ）求数列的通项公式；

设数列的各项都是正数，且对任意都有成立，其中是数列的前n项和．

（Ⅱ）过点F的直线l与交于M、N两点，与交于P、Q两点，若，求直线l的方程．

（21）（本小题满分12分）

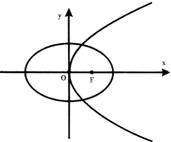（Ⅰ）求椭圆的方程；

设椭圆的中心在原点，其右焦点与抛物线：的焦点F重合，过点F与x轴垂直的直线与交于A、B两点，与交于C、D两点，已知．

（Ⅰ）求证：A₁B∥平面AC₁D；

（Ⅱ）求二面角C-AC₁-D的大小.

（20）（本小题满分12分）

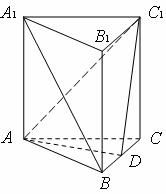如图，在正三棱柱ABC-A₁B₁C₁中，AB=AA₁，D是BC上一点，且AD⊥C₁D.

有一种舞台灯，外形是正六棱柱，在其每一个侧面上安装5只颜色各异的彩灯，假若每只灯正常发光的概率为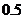. 若一个面上至少有3只灯发光，则不需要维修，否则需要更换这个面.假定更换一个面需要100元，用ξ表示维修一次的费用.

（Ⅰ）求恰好有2个面需要维修的概率；

（Ⅱ）写出ξ的分布列，并求ξ的数学期望.

（19）（本大题满分12分）