求证：PC?PDPE?PF．

    (2)如图2，若直线MN与⊙0相离．(1)中的其余条件不变，那么(1)中的结论还成立吗?若成立，请给予证明；若不成立，请说明理由．

    (3)在图3中，直线MN与⊙0相离，且与⊙0的直径AB垂直，垂足为P．①请按要求

画出图形：画⊙0的割线PCD(PC<PD)，直线BC与MN交于E，直线BD与MN交于F．②能否仍能得到(1)中的结论?请说明理由．

25．(本题满分12分)

    (1)如图1，直线MN与⊙0相交，且与⊙0的直径AB垂直，垂足为P，过点P的直线与⊙0交于C、D两点，直线AC交MN于点E，直线AD交MN于点F．

24．(本题满分11分)

    为庆祝“六一”儿童节，某市中小学统一组织文艺汇演．甲、乙两所学校共92人(其中甲校人数多于乙校人数，且甲校人数不够90人)准备统一购买服装参加演出，下面是某服装厂给出的演出服装的价格表：

购买服装的套数

1套至45套

46套至90套

91套及以上

每套服装的价格

    60元

    50元

    40元

如果两所学校分别单独购买服装，一共应付5000元．

   （1）如果甲、乙两校联合起来购买服装，那么比各自购买服装共可以节省多少钱?

   （2）甲、乙两所学校各有多少学生准备参加演出?

   （3)如果甲校有lO名同学抽调去参加书法绘画比赛不能参加演出，请你为两所学校设计一种最省钱的购买服装方案．

    (2)园林小路，曲径通幽，如图2所示，小路由白色的正方形理石和黑色的三角形理石铺成．已知中间的所有正方形的面积之和是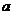平方米，内圈的所有三角形的面积之和是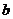平方米，这条小路一共占地多少平方米?

23．(本题满分10分)    

(1)如图1，以△ABC的边AB、AC为边分别向外作正方形ABDE和正方形ACFG，连结EG，试判断△ABC与△AEG面积之间的关系，并说明理由．

22. (本题满分9分)

某风景区内有一古塔AB，在塔的北面有一建筑物，冬至日的正午光线与水平面的夹角是30°，此时塔在建筑物的墙上留下了高3米的影子CD；而在春分日正午光线与地面的夹角是45°，此时塔尖A在地面上的影子E与墙角C有15米的距离(B、E、C在一条直线上)，

求塔AB的高度(结果保留根号)．

问题（2）：请你另取一个适当的正整数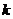，其它条件不变，不解方程，改求的值.