练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

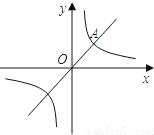
    如图，直线y=x与双曲线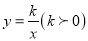的一个交点为A，且OA=2，则k的值为　 　．

    2． 【解析】∵点A在直线y=x，且OA=2， ∴点A的坐标为 ， 把代入得， ， ∴k=2.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年安徽省中考数学三模试卷 题型：填空题

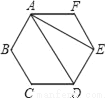
    如图，AD、AE是正六边形的两条对角线，不添加任何辅助线，请写出两个正确的结论：

    （1）_____；

    （2）_____．（只写出两个你认为正确的结论即可）．

    三角形AFE是等腰三角形 四边形ABCD是等腰梯形 【解析】示例三角形AFE是等腰三角形；四边形ABCD是等腰梯形．答案不唯一．

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2018届九年级上学期期末考试数学试卷 题型：解答题

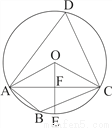
    如图，四边形ABCD 是⊙O的内接四边形，∠ABC=2∠D,连接OA，OC,AC

    （1）求∠OCA的度数 （2）如果OE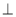AC于F,且OC=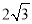, 求AC的长

    (1) 30°;(2)6 【解析】试题分析：（1）由圆内接四边形的性质得到∠ABC+∠D=180°，即可得到∠D的度数，再由圆周角定理得到∠AOC的度数，根据等腰三角形的性质即可得到∠OCA的度数； （2）由30°角直角三角形三边关系可以得到OF，CF的长，再由垂径定理即可得到结论． 试题解析：解：（1）∵四边形ABCD 是⊙O的内接四边形，∴∠ABC+ ∠D=180°． ...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2018届九年级上学期期末考试数学试卷 题型：单选题

    在平面直角坐标系中，点P（2，一 4）关于原点对称的点的坐标是（ ）

    A. （2,4 ） B. （一2，4） C. （一2，一4） D. （一4，2）

    B 【解析】【解析】 点P（2，一 4）关于原点对称的点的坐标是（－2，4）．故选B．

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市东海实验学校2017年中考数学模拟试卷 题型：解答题

    某高科技产品开发公司现有员工50名，所有员工的月工资情况如下表：

    员工

    管理人员

    普通工作人员

    人员结构

    总经理

    部门经理

    科研人员

    销售人员

    高级技工

    中级技工

    勤杂工

    员工数（名）

    1

    3

    2

    3

    24

    1

    每人月工资（元）

    21000

    8400

    2025

    2200

    1800

    1600

    950

    请你根据上述内容，解答下列问题：

    （1）该公司“高级技工”有　 　名；

    （2）所有员工月工资的平均数x为2500元，中位数为　 　元，众数为　 　元；

    （3）小张到这家公司应聘普通工作人员．请你回答右图中小张的问题，并指出用（2）中的哪个数据向小张介绍员工的月工资实际水平更合理些；

    （4）去掉四个管理人员的工资后，请你计算出其他员工的月平均工资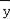（结果保留整数），并判断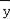能否反映该公司员工的月工资实际水平．

    （1）16人；（2）工中位数是1700元；众数是1600元；（3）用1700元或1600元来介绍更合理些．（4）能反映该公司员工的月工资实际水平． 【解析】试题分析：（1）用总人数50减去其它部门的人数；（2）根据中位数和众数的定义求解即可；（3）由平均数、众数、中位数的特征可知，平均数易受极端数据的影响，用众数和中位数映该公司员工的月工资实际水平更合适些；（4）去掉极端数据后平均数可以反映...

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市东海实验学校2017年中考数学模拟试卷 题型：单选题

    一名模型赛车手遥控一辆赛车，先前进1m，然后，原地逆时针方向旋转角a(0°<α<180°)。被称为一次操作．若五次操作后，发现赛车回到出发点，则角α为 ( )

    A. 7 2° B. 108°或14 4° C. 144° D. 7 2°或144°

    D 【解析】试题分析：因为赛车五次操作后回到出发点，五次操作一种是“正五边形“二种是“五角星“形，根据α最大值小于180°，经过五次操作，绝对不可能三圈或三圈以上．一圈360°或两圈720度．分别用360°和720°除以5，就可以得到答案． 【解析】 360÷5=72°， 720÷5=144°． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市东海实验学校2017年中考数学模拟试卷 题型：单选题

    下图中①表示的是组合在一起的模块，在②③④⑤四个图形中，是这个模块的俯视图的是（　　）

    A. ② B. ③ C. ④ D. ⑤

    A 【解析】②是该几何体的俯视图；③是该几何体的左视图和主视图；④、⑤不是该几何体的三视图. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省徐州市中考数学一模试卷 题型：填空题

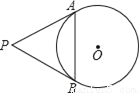
    如图，PA、PB是⊙O的切线，切点分别为A、B，已知⊙O的半径为2，∠P=60°，则弦AB的长为_____．

    【解析】连接AO，并延长交⊙O于C，连接BC， ∵PA、PB是⊙O的切线， ∴PA=PB， 又∵∠P=60°， ∴∠PAB=60°； 又∵AC是圆的直径， ∴CA⊥PA，∠ABC=90°， ∴∠CAB=30°， 而AC=4， ∴在Rt△ABC中，cos∠CAB=cos30°=，即， ∴AB=4×． 故答案为： ．

    查看答案和解析>>

    科目：初中数学 来源：四川省遂宁市2017-2018学年八年级上学期教学水平监测数学试卷 题型：解答题

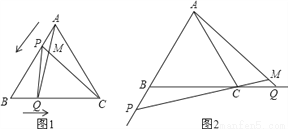
    如图1，点P、Q分别是等边△ABC边AB、BC上的动点（端点除外），点P从顶点A、点Q从顶点B同时出发，且它们的运动速度相同，连接AQ、CP交于点M．

    （1）△ABQ与△CAP全等吗？请说明理由；

    （2）当点P、Q分别在AB、BC边上运动时，∠QMC变化吗？若变化，请说明理由；若不变，求出它的度数．

    （3）如图2，若点P、Q在运动到终点后继续在AB、BC的延长线上运动，直线AQ、CP交点为M，则∠QMC变化吗？若变化，请说明理由；若不变，则求出它的度数．

    （1）全等，理由见解析； (2)点P、Q在运动的过程中，∠QMC不变，60°；（3）点P、Q在运动到终点后继续在射线AB、BC上运动时，∠QMC不变，120°. 【解析】试题分析：(1)、根据等边三角形可得∠ABQ=∠CAP，AB=CA，根据速度相同可得AP=BQ，从而得出三角形全等；(2)、根据△ABQ≌△CAP得出∠BAQ=∠ACP，然后根据∠QMC=∠BAQ+∠MAC得出答案；(3)、...

    查看答案和解析>>

    同步练习册答案