
计算:
(1) (-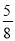 -
-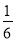 +
+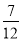 )×24+5; (2)-32-(1-
)×24+5; (2)-32-(1-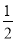 )÷3×|3-(-3)2|.
)÷3×|3-(-3)2|.
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源:山东省泰安市宁阳县2017-2018学年九年级上学期期末质量检测数学试卷 题型:填空题
在平面直角坐标系中,点C、D的坐标分别为C(2,3)、D(1,0),现以原点为位似中心,将线段CD放大得到线段AB.若点D的对应点B在x轴上且OB=2,则点C的对应点A的坐标为______________________________.
(4,6)或(﹣4,﹣6). 【解析】已知点D(1,0),点D的对应点B在x轴上,且OB=2,所以位似比为2,即可得点A的坐标为(2×2,3×2)或[2×(-2),3×(-2)],即点A的坐标为(4,6)或(-4,-6).查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
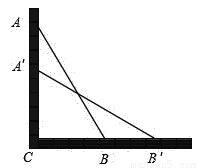
如图,一架长2.5m的梯子AB斜靠在墙AC上,∠C=90°,此时,梯子的底端B离墙底C的距离BC为0.7m.
(1)求此时梯子的顶端A距地面的高度AC;
(2)如果梯子的顶端A下滑了0.9m,那么梯子的顶端B在水平方向上向右滑动了多远?
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
下列各式中,计算正确的是( )
A. 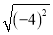 =4 B.
=4 B. 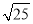 =±5 C.
=±5 C. 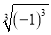 =1 D.
=1 D. 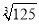 =±5
=±5
查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
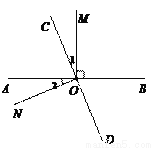
如图,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,判断ON与CD的位置关系,并说明理由.
(2)若∠BOC=4∠1,求∠MOD的度数.
查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
代数式x2﹣2x=3,则代数式3x2﹣6x﹣1的值为__________.
8 【解析】试题分析:根据题意,由乘法分配律可得3x2﹣6x﹣1=3(x2﹣2x)-1,然后把x2﹣2x=3整体代入即可得3x2﹣6x﹣1=3×3-1=8.查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
某工程甲独做需12天完成,乙独做需8天完成.现由甲先做3天,乙再合做共同完成.若设完成此项工程共需x天,则下列方程正确的是( )
A. 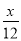 +
+ =1 B.
=1 B.  +
+ =1 C.
=1 C. 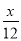 +
+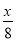 =1 D.
=1 D. 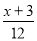 +
+ =1
=1
查看答案和解析>>
科目:初中数学 来源:湖北省襄阳市襄城区2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
用一根长60m的绳子围出一个长方形,使它的长是宽的1.5倍,那么这个长方形的长是_________m.
18 【解析】试题解析:设长方形的宽为xm,则长方形的长为1.5xm. 根据题意,得2(x+1.5x)=60, 解得,x=12. 所以长为12×1.5=18(m). 故答案为:18.查看答案和解析>>
科目:初中数学 来源:2017-2018年福建厦门市八年级上册数学期末质量检测试卷 题型:解答题
如图,在△ABC中,AB=AC, 点M在△ABC内,点P在线段MC上,∠ABP=2∠ACM.

(1)若∠PBC=10°,∠BAC=80°,求∠MPB的值
(2)若点M在底边BC的中线上,且BP=AC,试探究∠A与∠ABP之间的数量关系,并证明.
(1) ∠MPB=40°;(2) ∠BAC+∠ABP=120°.证明见解析 【解析】试题分析:(1)由AB=AC,∠BAC=80°,可求∠ABC=∠ACB=50°,又∠PBC=10°,∠ABP=2∠ACM,可求∠BCM=30°,由三角形外角的性质可求出结果; (2)过点A作底边BC的中线AD,连接BM,由等腰三角形三线合一的性质可得∠CAM=∠BAM,从而可证△ABM≌△ACM.进而证...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com