
有一个反比例函数的图象,在第二象限内函数值随着自变量的值增大而增大,这个函数的表达式可能是(写出一个即可):________________.
答案不唯一,k<0即可 【解析】∵反比例函数的图象的一个分支在第二象限, ∴在反比例函数中, , ∴这样的函数不是唯一的,只要即可,如: .科目:初中数学 来源:安徽省2017-2018学年度七年级第一学期人教版数学期末自测试卷(二) 题型:单选题
-7的倒数是( )
A. 7 B. 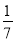 C. -7 D. -
C. -7 D. -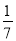
查看答案和解析>>
科目:初中数学 来源:辽宁省2018届九年级(上)期末模拟数学试卷 题型:填空题
小华与父母从合肥乘车去无为县米公祠(北宋大书法家米芾故居)参观,车厢里每排有左、中、右三个座位,小华一家三口随意坐某排的三个座位,则小华恰好坐在中间的概率是 .
. 【解析】 试题分析:共有三个座位,小华有三种坐法;小华恰好坐在中间是其中一种情况;故则小华恰好坐在中间的概率是. 故答案是.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期初三数学期末试卷 题型:解答题
数学课上老师提出了下面的问题:
在正方形ABCD对角线BD上取一点F,使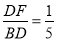 .小明的做法如下:如图,
.小明的做法如下:如图,
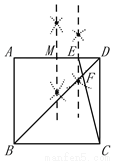
①应用尺规作图作出边AD的中点M;
②应用尺规作图作出MD的中点E;
连接EC,交BD于点F.
所以F点就是所求作的点.
请你判断小明的做法是否正确,并说明理由.
正确,理由见解析. 【解析】试题分析: 由作图易得,再证△DEF∽△BFC可得,由此即可得到,从而说明小明的做法正确. 试题解析: 小明的做法正确,理由如下: 由做法可知M为AD的中点,E为MD的中点, ∴, ∵四边形ABCD是正方形, ∴AD=BC,ED∥BC, ∴△DEF∽△BFC, ∴=, ∵AD=BC ∴==, ...查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期初三数学期末试卷 题型:填空题
阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:△OAB.
求作:⊙O,使⊙O与△OAB的边AB相切.

小明的作法如下:
如图,①取线段OB的中点M;以M为圆心,MO为半径作⊙M,与边AB交于点C;
②以O为圆心,OC为半径作⊙O;
所以,⊙O就是所求作的圆.
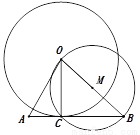
请回答:这样做的依据是__________________________________________________.
圆的定义,直径的定义,直径所对的圆周角为90°,到线段两端点距离相等的点在线段的垂直平分线上,经过半径的外端并且垂直于这条半径的直线是圆的切线. 【解析】∵要作出线段OB的中点M, ∴需作线段OB的垂直平分线,交OB于点M, ∴OM=MB(线段垂直平分线上的点到线段两端的距离相等); ∵以M为圆心,MO为半径作⊙M(圆的定义), ∴OB是⊙M的直径(直径定义), ...查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期初三数学期末试卷 题型:单选题
网球单打比赛场地宽度为8米,长度在球网的两侧各为12米,球网高度为0.9米(如图AB的高度).中网比赛中,某运动员退出场地在距球网14米的D点处接球,设计打出直线穿越球,使球落在对方底线上C处,用刁钻的落点牵制对方.在这次进攻过程中,为保证战术成功,该运动员击球点高度至少为( )

A. 1.65米 B. 1.75米 C. 1.85米 D. 1.95米
D 【解析】如图,由题意可知,AB∥DE, ∴△CBA∽△CDE, ∴, ∵AB=0.9,CB=12,CD=CB+BD=26, ∴, ∴12DE=0.9×26, ∴DE=1.95(米). 故选D.查看答案和解析>>
科目:初中数学 来源:江苏省南通市崇川区2015-2016学年八年级上学期期末考试数学试卷 题型:解答题
选取二次三项式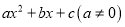 中的两项,配成完全平方式的过程叫配方.
中的两项,配成完全平方式的过程叫配方.
例如:①选取二次项和一次项配方: 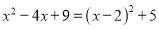 ;
;
②选取二次项和常数项配方: 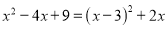 ,或
,或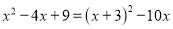
③选取一次项和常数项配方: 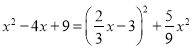
根据上述材料,解决下面问题:
(1)写出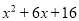 的两种不同形式的配方;
的两种不同形式的配方;
(2)已知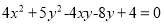 ,求
,求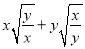 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:江苏省南通市崇川区2015-2016学年八年级上学期期末考试数学试卷 题型:单选题
点P是等边三角形ABC所在平面上一点,若P和△ABC的三个顶点所组成的△PAB、△PBC、△PAC都是等腰三角形,则这样的点P的个数为( )
A.1 B.4 C.7 D.10
D. 【解析】 试题分析:①以A为圆心,AB为半径画弧交BC的垂直平分线于点P1,P2两点;以B为圆心,AB为半径弧交BC的垂直平分线于点P3,这样在AB的垂直平分线上有三点, ②同样在AC,BC的垂直平分线上也分别有三点; ③还有一点就是AB,BC,AC三条边的垂直平分线的交点; 共3+3+3+1=10点. 故选D.查看答案和解析>>
科目:初中数学 来源:广东省2017-2018学年七年级(上)期末模拟数学试卷 题型:解答题
为体现社会对教师的尊重,教师节这一天上午,出租车司机小聪在东西方向的公路上免费接送老师.如果规定向东为正,向西为负,出租车的行程如下(单位:千米):+15,-4,+13,―10,―12,+3,―13,―17.
(1)出车地记为0,最后一名老师送到目的地时,小聪距出车地点的距离是多少?
(2)若汽车耗油量为0.1升/千米,这天上午汽车共耗油多少升?
(1)最后一名老师送到目的地时,小王在出车地点的西面25千米处. (2)这天上午汽车共耗油8.7升. 【解析】 试题分析:(1)由已知,出车地位0,向东为正,向西为负,则把表示的行程距离相加所得的值,如果是正数,那么是距出车地东面多远,如果是负数,那么是距出车地东面多远. (2)不论是向西(负数)还是向东(正数)都是出租车的行程.因此把它们行程的绝对值相加就是出租车的全部行...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com