
不改变分式的值,使式子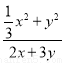 分子中的系数不含有分数,下列四个选项中正确的是( )
分子中的系数不含有分数,下列四个选项中正确的是( )
A. 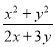 B.
B. 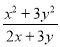 C.
C. 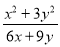 D.
D. 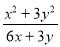
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:江苏省无锡市2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
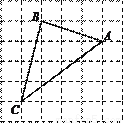
如图,所有小正方形的边长都为1,A、B、C都在格点上.
(1)过点B画直线AC的垂线,垂足为G;
(2)比较BC与BG的大小:BC_______BG,理由是________________;
(3)已知AC=5,求BG的长.
查看答案和解析>>
科目:初中数学 来源:湖北省襄阳市襄城区2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
组成多项式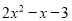 的单项式是下列几组中的( )
的单项式是下列几组中的( )
A. 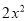 ,x,3 B.
,x,3 B. 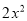 ,-x,-3
,-x,-3
C. 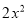 ,x,-3 D.
,x,-3 D. 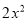 ,-x,3
,-x,3
查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
若关于x的分式方程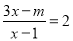 的解是正数,则m的取值范围为_______.
的解是正数,则m的取值范围为_______.
查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
若点P(-3,4)和点Q(a,b)关于 轴对称,则2a+b=_______.
轴对称,则2a+b=_______.
查看答案和解析>>
科目:初中数学 来源:2017-2018年福建厦门市八年级上册数学期末质量检测试卷 题型:解答题
已知一组数9,17,25,33,…,(8n+1)(从左往右数,第1个数是9,第2个数是17,第3个数是25,第4个数是33,依此类推,第n个数是8n+1).设这组数的前n个数的和是sn.
(1)第5个数是多少?并求1892—s5的值;
(2)若n满足方程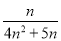 =
=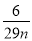 ,则
,则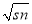 的值是整数吗?请说明理由.
的值是整数吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源:2017-2018年福建厦门市八年级上册数学期末质量检测试卷 题型:填空题
如图,在河流的同岸有A,B两个村庄,要在河岸l上确定相距a米的两点C,D(点D在点C的右边),使得AC+BD的和最小.若用作图的方式来确定点C,则确定点C的步骤是______________.

查看答案和解析>>
科目:初中数学 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价九年级数学 题型:解答题
某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为20℃的条件下生长最快的新品种.图示是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是反比例函数y=一的图象上一部分,请根据图中信息解答下列问题
(1)恒温系统在这天保持大棚内温度20℃的时间有多少小时?
(2)求k的值;
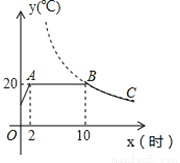
(3)当x=20时,大棚内的温度约为多少度?
【答案】(1)8小时;(2)200;(3)当x=20时,大棚内的温度约为10℃.
【解析】试题分析:(1)根据图象直接得出大棚温度20℃的时间为10﹣2=8(小时);
(2)利用待定系数法求反比例函数解析式即可;
(3)将x=20代入函数解析式求出y的值即可.
试题解析:(1)恒温系统在这天保持大棚温度20℃的时间为:10﹣2=8(小时);
(2)∵点B(10,20)在双曲线y=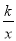 上,
上,
∴20=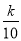 ,
,
∴解得:k=200;
(3)当x=20时,y=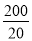 =10,
=10,
所以当x=20时,大棚内的温度约为10℃.
【点睛】本题考查了反比例函数的应用,正确地求得反比例函数的解析式是解题的关键.
【题型】解答题
【结束】
25
某研究所将某种材料加热到1000℃时停止加热,并立即将材料分为A、B两组,采用不同工艺做降温对比实验,设降温开始后经过x min时,A、B两组材料的温度分别为yA℃、yB℃,yA、yB与x的函数关系式分别为yA=kx+b,yB=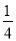 (x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.
(x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.
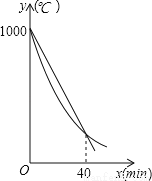
(1)分别求yA、yB关于x的函数关系式;
(2)当A组材料的温度降至120℃时,B组材料的温度是多少?
(3)在0<x<40的什么时刻,两组材料温差最大?
(1)yA=﹣20x+1000; (2)B组材料的温度是164℃; (3)当x=20时,两组材料温差最大为100℃. 【解析】试题分析:(1)首先求出yB函数关系式,进而得出交点坐标,即可得出yA函数关系式;(2)首先将y=120代入求出x的值,进而代入yB求出答案;(3)得出yA-yB的函数关系式,进而求出最值即可. 试题解析:(1)由题意可得出:yB=(x﹣60)2+m...查看答案和解析>>
科目:初中数学 来源:广东省深圳市龙岗区2017-2018学年度第一学期期末质量检测八年级数学试卷 题型:单选题
甲,乙,丙,丁四名跳远运动员选拔塞成绩的平均数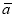 与方差
与方差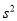 如下表所示:
如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数 | 561 | 561 | 560 | 560 |
方差 | 3.5 | 15.5 | 3.5 | 16.5 |
根据表中数据,要从中选一名成绩好又发挥稳定的运动员参赛,应该选择( )
A. 甲 B. 乙 C. 丙 D. 丁
A 【解析】试题解析:∵甲的方差是3.5,乙的方差是3.5,丙的方差是15.5,丁的方差是16.5, ∴S2甲=S2乙查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com