练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图,AD是△ABC中BC边上的中线.

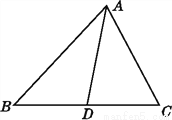
    试说明:AD<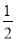 (AB+AC).

    答案见解析 【解析】试题分析：延长AD到E，使DE=AD，连BE，则△ACD≌△EBD，由此可得BE=AC，进而在△ABE中利用三角形三边关系，即可得出结论． 试题解析：【解析】 如图，延长AD至点E，使DE=AD，连接BE． ∵AD是△ABC中BC边上的中线，∴CD=BD． 在△ACD与△EBD中，∵CD=BD，∠ADC=∠EDB，AD=ED，∴△ACD≌△EBD(SA...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级数学下2.1.2 垂线的定义与性质 同步练习 题型：单选题

    如图,过点P作直线l的垂线和斜线,叙述正确的是(　　)

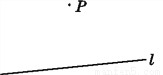
    A. 都能作且只能作一条

    B. 垂线能作且只能作一条,斜线可作无数条

    C. 垂线能作两条,斜线可作无数条

    D. 均可作无数条

    B 【解析】∵过一点有且只有一条直线与已知直线垂直；而过一点可以做无数条斜线. 故选：B.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 第一章　整式的乘除 单元测试卷 题型：填空题

    如果a与b异号，那么(a＋b)2与(a－b)2的大小关系是___________________.

    (a＋b)2＜(a－b)2 【解析】(a+b)2?(a?b)2=a2+2ab+b2?(a2?2ab+b2=4ab， 而ab<0， ∴(a+b)2?(a?b)2<0. 故答案为：(a＋b)2＜(a－b)2.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下3.2 用关系式表示的变量间关系 同步练习 题型：解答题

    有一种粗细均匀的电线,为了确定其长度,从一捆上剪下1 m,称得它的质量是0.06 kg.

    (1)写出这种电线长度与质量之间的关系式;

    (2)如果一捆电线剪下1 m后的质量为b kg,请写出这捆电线的总长度.

    【答案(1)l= (2) m 【解析】试题分析： （1）设这捆电线的质量为kg，由题意可知，这种电线1米的质量为0.06kg，由此可得这捆电线的长度米； （2）由（1）可得，剪下1米后的电线的长度为： 米，由此可得这捆电线的总长度为： 米. 试题解析： （1）设电线的长度为米，质量为m kg，则这捆电线的长度为： ； （2）由（1）可知，剩下的kg的电线的长度为...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下3.2 用关系式表示的变量间关系 同步练习 题型：单选题

    百货大楼进了一批花布,出售时要在进价(进货价格)的基础上加一定的利润,其长度x与售价y如下表:

    长度x/m

    1

    2

    3

    4

    …

    售价y/元

    8+0.3

    16+0.6

    24+0.9

    32+1.2

    …

    下列用长度x表示售价y的关系式中,正确的是(　　)

    A. y=8x+0.3 B. y=(8+0.3)x C. y=8+0.3x D. y=8+0.3+x

    B 【解析】依题意得y＝(8＋0.3)x．故选B．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.3.3 用“边角边”判定三角形全等 同步练习 题型：解答题

    如图,点O是线段AB和线段CD的中点.试说明:

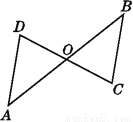
    (1)△AOD≌△BOC;

    (2)AD∥BC.

    (1)答案见解析;(2)答案见解析 【解析】试题分析：（1）由中点定义，得到AO=BO，CO=DO，从而通过SAS证明△AOD≌△BOC； （2）由（1）中结论，可以得到∠A=∠B，再由内错角相等，两直线平行即可得出结论． 试题解析：【解析】 (1)∵点O是线段AB和线段CD的中点，∴AO=BO，CO=DO． 在△AOD和△BOC中，∵AO=BO，∠AOD=∠BOC，DO...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.3.3 用“边角边”判定三角形全等 同步练习 题型：单选题

    如图,AA',BB'表示两根长度相同的木条,若O是AA',BB'的中点,经测量AB=9 cm,则容器的内径A'B'为(　　)

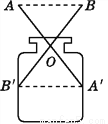
    A. 8 cm B. 9 cm C. 10 cm D. 11 cm

    B 【解析】【解析】 由题意知：OA=OA′，∠AOB=∠A′OB′，OB=OB′，∴△AOB≌△A′OB′，∴A′B′=AB=9cm．故选B．

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第四章4.4用尺规作三角形课时练习 题型：解答题

    如图，有分别过A、B两个加油站的公路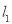、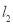相交于点O，现准备在∠AOB内建一个油库，要求油库的位置点P满足到A、B两个加油站的距离相等，而且P到两条公路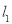、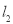的距离也相等．请用尺规作图作出点P（不写作法，保留作图痕迹）

    作图见解析． 【解析】 试题分析: 到A、B两个加油站的距离相等的点在线段AB的垂直平分线上；到两条公路的距离相等的点在两条公路的夹角的角平分线上． 试题解析：如图：

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.3.1 用“边边边”判定三角形全等 同步练习 题型：解答题

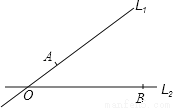
    如图：在△ABC中,AC=BC,D是AB上的一点,AE⊥CD于点E,BF⊥CD于点F,若CE=BF,AE=EF+BF.试判断AC与BC的位置关系,并说明理由.

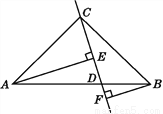
    AC⊥BC，理由见解析. 【解析】试题分析：根据AE⊥CD，BF⊥CD，得到∠AEC=∠BFC=90°，由于CF=EE+CF，CE=BF，得到CF=EF+BF，于是得到AE=CF，证得Rt△ACE≌Rt△CBF，得出∠BCF=∠CAE，然后根据∠ACB=∠BCF+∠ACE=∠CAE+∠AEC=90°，即可得到结论． 试题解析:AC⊥BC. 理由如下：∵AE⊥CD，BF⊥CD， ...

    查看答案和解析>>

    同步练习册答案