
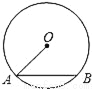
(3分)如图,AB是⊙O的弦,半径OA=2,sinA=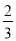 ,则弦AB的长为( )
,则弦AB的长为( )
A. 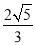 B.
B. 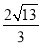 C. 4 D.
C. 4 D. 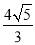
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源:河北省唐山市路北区2017-2018学年七年级(上)期末复习数学试卷 题型:解答题
课外阅读课上.老师将一批书分给各小组.若每小组8本.则还剩余3本:若每小组9本.则还缺2本.问有几个小组.(根据题意设未知数,只列出方程即可)
8x+3=9x﹣2. 【解析】试题分析:设有个小组,则课外书的本数为,或表示为,由此联立得出方程即可. 试题解析:设有个小组,根据题意可得:查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学模拟试卷(三) 题型:单选题
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点P以每秒一个单位的速度沿着B﹣C﹣A运动,⊙P始终与AB相切,设点P运动的时间为t,⊙P的面积为y,则y与t之间的函数关系图象大致是( )
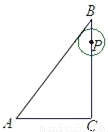
A. 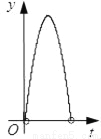 B.
B. 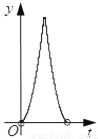 C.
C. 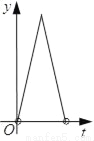 D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学模拟试卷 题型:解答题
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.
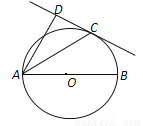
(1)求证:AD⊥CD;
(2)若AD=2,AC=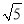 ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学模拟试卷 题型:填空题
在平面直角坐标系中,入射光线经过y轴上点A(0,5),由x轴上点C反射,反射光线经过点B(﹣4,1),则点C的坐标为_____.
(﹣,0) 【解析】试题解析:A(0,5)关于x轴的对称点的坐标是(0,?5), 设经过B与(0,?5)的函数解析式是y=kx+b, 根据待定系数法,就可以求出函数解析式是 令y=0,解得 因而点C的坐标为 故答案为:查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学模拟试卷 题型:单选题
直线y=﹣2(x﹣1)+1与水平线所夹锐角的余弦是( )
A. 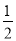 B. ﹣
B. ﹣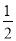 C.
C. 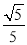 D. ﹣
D. ﹣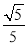
查看答案和解析>>
科目:初中数学 来源:2017年天津109中中考数学模拟试卷 题型:解答题
(6分)如图,点P为△ABC的内心,延长AP交△ABC的外接圆于D,在AC延长线上有一点E,满足AD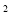 =AB·AE,求证:DE是⊙O的切线.
=AB·AE,求证:DE是⊙O的切线.
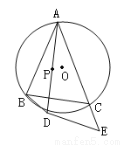
第20题图
证明略 【解析】证明:连结DC,DO并延长交⊙O于F,连结AF.∵AD=AB·AE,∠BAD=∠DAE,∴△BAD∽△DAE,∴∠ADB=∠E. 又∵∠ADB=∠ACB,∴∠ACB=∠E,BC∥DE,∴∠CDE=∠BCD=∠BAD=∠DAC,又∵∠CAF=∠CDF,∴∠FDE=∠CDE+∠CDF=∠DAC+∠CDF=∠DAF=90°,故DE是⊙O的切线查看答案和解析>>
科目:初中数学 来源:2017年天津109中中考数学模拟试卷 题型:单选题
中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示为( )
A. 44×108 B. 4.4×109 C. 4.4×108 D. 4.4×1010
B 【解析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数. 【解析】 4 400 000 000=4.4×109, 故选B.查看答案和解析>>
科目:初中数学 来源:浙江省杭州市2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
如图,已知半径OD与弦AB互相垂直,垂足为点C,若AB=8,CD=3,则⊙O的半径为( )
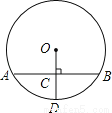
A. 4 B. 5 C. 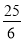 D.
D. 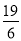
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com